Sic Bo - Laske kertoimet ja voita | Video

Hei kaikki, täällä Mike.

Opit laskemaan kertoimet Sic Bo -pelissä. Lyhyesti sanottuna Sic Bo on hyvin ikivanha kiinalainen peli, joka perustuu kolmen nopan heittämiseen. Pelissä on laaja valikoima panostusvaihtoehtoja.

Mitä aion tehdä :

Jaan tämän aiheen kahteen videoon, koska kaikki foorumillani valittavat, että videoni ovat liian pitkiä. Tässä ensimmäisessä osassa selitän, kuinka lasketaan minkä tahansa annetun kokonaisluvun 3:sta 18:aan heittämisen todennäköisyys kolmella nopalla, sekä kuinka todennäköisyys heittää minkä tahansa nopan sivun tulos 0, 1, 2 tai 3.

Kun olemme aseistautuneet vastauksilla näihin kysymyksiin…

...voimme siirtyä toiseen osaan ja analysoida, millaista arvoa saat kaikilla Sic Bon erilaisilla panostuksilla.

Vastataanpa kysymykseen : "Mikä on todennäköisyys heittää mikä tahansa annettu kokonaistulos kolmella kuusisivuisella nopalla?" Tämä tekniikka, jonka aion näyttää teille, toimii mille tahansa määrälle noppia.

Haluan antaa tunnustusta Robert Goodhandille Somersetista, Isosta-Britanniasta, tästä hankalasta pienestä tekniikasta. Sitä käsitellään Kysy velholta -kolumnissani 264. Aion jakaa sen kanssanne nyt.

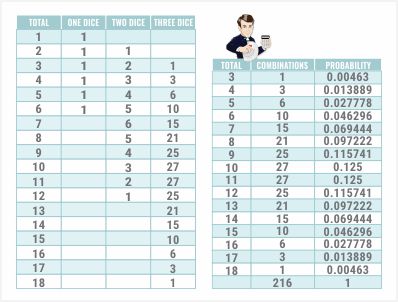
Ensin meidän tarvitsee määritellä viisi tyhjää ruutua. Näet miksi hetken kuluttua. Nyt aion listata kaikki kokonaisluvut 1:stä 18:aan. Yhdellä nopalla on tietysti vain yksi tapa heittää luku 1, 2 tai 6.

Jokaisella sivulla on yksi sivu, joten se on melko ilmeistä. Kahdella nopalla sinun on laskettava vasemmanpuoleisen sarakkeen, tässä tapauksessa B-sarakkeen, summa alkaen yhdestä vasemmalla olevasta ruudusta ja päättyen sitten viiteen sen yläpuolella olevaan ruuduen.

Juuri nyt kyseessä olevassa tapauksessa…

...Työskentelen solun C8 kanssa. Tämä osoittaa, kuinka monta kertaa kahdella nopalla voi heittää yhteensä kaksi. Lasken solujen B2–B7 arvojen summan. Jos solu on tyhjä, Excel olettaa oikein, että se on nolla.

Kopioin ja liitän sen alas kaikkiin mahdollisiin kokonaismääriin aina lukuun 12 asti. Näet, että jos lukuja on yhteensä kaksi, on yksi tapa tehdä se. Jos lukuja on yhteensä kolme, on kaksi tapaa. Jos lukuja on yhteensä neljä, on kolme tapaa.

No miksi tämä toimii?

Tarkastellaanpa kokonaissummaa kaksi. Jotta kokonaissummaksi saadaan kaksi, ensimmäisen nopan on oltava yksi ja toisen nopan on oltava yksi. Ensimmäinen noppa voi olla yksi vain yhdellä tavalla, ja ilmeisesti toinenkin noppa voi olla yksi vain yhdellä tavalla. Kokonaissummaksi kolme on kaksi tapaa.

On yksi tapa , jolla ensimmäinen noppa voi olla ykkönen ja toinen noppa on kaksi , sekä yksi tapa, jolla ensimmäinen noppa voi olla kaksi ja toinen ykkönen. Jotta lukuja olisi yhteensä neljä, ensimmäisen nopan on oltava yksi-kolme.

Yhteensä viisi...

Ensimmäisen nopan tulosten on oltava yhteensä yhdestä neljään. Niin kauan kuin ensimmäisen nopan tulos on hyväksyttävällä alueella, seuraava noppa voi saavuttaa minkä tahansa kokonaistuloksen, josta puhut.

Siirrytään kolmeen noppaan

Se on täsmälleen sama tekniikka. Voimme vain kopioida ja liittää saman kaavan. Voisin ottaa tämän mistä tahansa juuri tekemästämme alueesta. Teen sen vain tässä, kopioin ja liitän sen yhden solun oikealle ja kopioin ja liitän sen alas. Siinä meillä on yhdistelmien lukumäärä mille tahansa kokonaissummalle 3:sta 18:aan kolmella nopalla.

Esimerkiksi:

On yksi tapa heittää yhteensä kolme, kolme tapaa heittää yhteensä neljä, kuusi tapaa heittää yhteensä viisi ja niin edelleen. Miksi tämä toimii? Saatat kysyä uudelleen. No, katsotaanpa esimerkiksi yhteensä seitsemän. Saadaksesi yhteensä seitsemän kolmella nopalla, se onnistuu, jos kahdella nopalla saadaan yhteensä kaksi ja sitten siihen lisätään viisi.

On yksi tapa, jolla kaksi ensimmäistä noppaa voivat olla yhteensä kaksi. Toinen tapa on, jos kaksi ensimmäistä noppaa voi olla yhteensä kolme ja kolmas noppa on sitten nelonen. Kuten juuri näimme, on kaksi tapaa, joilla kaksi ensimmäistä noppaa voi olla yhteensä kolme, ja on kolme tapaa, joilla kaksi ensimmäistä noppaa voi olla yhteensä neljä.

Saadaksesi yhteensä seitsemän …

...kahden ensimmäisen nopan summan on oltava kahdesta kuuteen. Näimme juuri, että tapahtumien kokonaismäärä olisi tässä summa yhdestä viiteen eli 15. Laitetaanpa tämä kaikki kätevään taulukkoon. Tässä on jälleen kokonaissumma.

Tässä ovat yhdistelmät :

Otetaanpa tuo kokonaissumma, 216. Luku näyttää tutulta. Ehkä se voisi olla kuusi kolmanteen potenssiin.

Lopuksi, löydetään kunkin kokonaissumman todennäköisyys:

Jaamme vain yhdistelmien lukumäärän kokonaismäärällä. Mikä tahansa annettu kokonaisluku 30:stä 18:aan on todennäköisyys heittää. Seuraavaksi tarkastellaan todennäköisyyttä heittää mikä tahansa nopan sivu nollasta kolmeen kertaan. Sic Bossa on kuusi erilaista panosta, yksi kutakin nopan sivua kohden.

Pelaaja voittaa yksi yhteen, jos valittu noppa heitettiin kerran, kaksi yhteen, jos se heitettiin kaksi kertaa, ja kolme yhteen, jos se heitettiin kolme kertaa. Nykyään monet ihmiset laskevat todennäköisyydet yhteen virheellisesti puhuessaan useista tapahtumista ja jokainen noppa on kuin itsenäinen tapahtuma.

Emme laske yhteen, vaan kerromme.

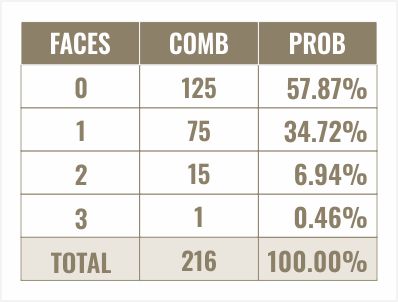
Rakastan ajatella asioita ensin yhdistelminä. Oletetaan esimerkiksi, että valitset vain kuusi. Kuinka monessa tapauksessa kuusi voi esiintyä kaikki kolme kertaa kolmella nopalla? No, se on yksinkertaisesti yksi. On vain yksi tapa, jolla se voi tapahtua, 6-6-6. Entä kaksi kertaa?

Esimerkiksi:

6-6-4 tai 2-6-6, 6-1-6. Kaksi nopista on kuutonen ja yksi niistä on jokin muu. Jokin muu voi olla mikä tahansa viidestä muusta sivusta, ja nämä jokin muu voi esiintyä millä tahansa kolmesta nopasta. Valitsemasi nopan sivu voi esiintyä kahdesti yhteensä 15 kertaa kolmesta nopasta.

Entä kuinka monella tavalla se voi ilmestyä kerran?

No, kaksi muuta noppaa, jotka eivät ole valitsemasi nopan sivu, voivat olla mitkä tahansa viidestä asiasta. Kerromme 5 x 5, koska toinen niistä voi olla mikä tahansa muu kuin kuutonen tai mikä tahansa valitsemasi sivu, ja toinenkin voi olla mikä tahansa muista viidestä sivusta.

Lopuksi…

...kerromme kolmella, koska valitsemasi noppa voi olla mikä tahansa kolmesta nopasta. Voit heittää valitsemasi nopan kerrallaan 5 x 5 x 3, mikä on 75. Esimerkkejä tästä: jos valitset nopan kuusi, se voi olla 6-1-2, 1-4-6, 1-6-5, 2-6-2, 6-1-3 ja niin edelleen.

Entä kuinka monessa tapauksessa ei ole mahdollista heittää yhtäkään valitsemastasi nopan sivusta?

No, jokainen kolmesta nopasta voi olla yksi viidestä asiasta. Viisi noppaa – tarkoitan kolme noppaa, viisi erilaista yhdistelmää jokaiselle valitsemasi sivun lisäksi on 5 x 5 x 5 yhdistelmää eli 125. Lasketaan kaikkien näiden yhdistelmien summa ja saadaan taas 216. Jälleen kerran, se on kuusi kolmanteen potenssiin, joten olen varmaan tehnyt jotain oikein.

Lopuksi, katsotaanpa todennäköisyyttä

Jaamme yksinkertaisesti yhdistelmien lukumäärän yhdistelmien kokonaismäärällä. Laitetaan tämä prosentin alle. Tässä näemme, että todennäköisyys sille, että valitsemasi kuva heitetään nolla kertaa, on 57,87 %, kerran 34,72 %, kaksi kertaa 6,94 % ja kolme kertaa 0,46 %.

Toivottavasti tämä oli selvää. Toivottavasti näemme toisessa osassa, jossa lasken monien eri Sic Bo -vetojen todennäköisyydet.

Kiitos katsomisesta.

Tämä dokumentti on luotu Instant HTML Editor -työkaluilla. Klikkaa tästä ja kokeile sitä ilmaiseksi.

Osa 2

Kirjoittanut: Michael Shackleford