Kysy velholta #426
Oletetaan, että sarjanumerot on numeroitu juoksevasti alkaen numerosta 1. Liikkeessä olevien kappaleiden enimmäismäärää ei tiedetä. Oletetaan, että satunnaisotos on n kappaletta, mikä on paras arvio sarjanumeron enimmäismäärästä?
Tykkään ajatella vastausta etsimällä sarjanumeroiden välisen keskimääräisen eron. Tämä lasketaan jakamalla suurin arvo otoskoolla. Jos esimerkiksi otoksen suurin kohde oli 1 000 ja otoskoko on 5, keskimääräinen väli on 1000/5=200. Lisää sitten tämä väli suurimpaan havaintoon saadaksesi arvioidun suurimman luvun. Tässä esimerkissä 1000+200 = 1200.
Tavallinen kaava, joka antaa saman luvun, on M*(k+1)/k, jossa M = maksimiarvo ja k = havaintojen lukumäärä. Esimerkissämme tämä antaa tulokseksi 1000*(6/5) = 1200.
ABCD on neliö, jonka sivun pituus on 10. Sen sisään on piirretty puoliympyrä ja neljännesympyrä, kuten seuraavassa kuvassa on esitetty.
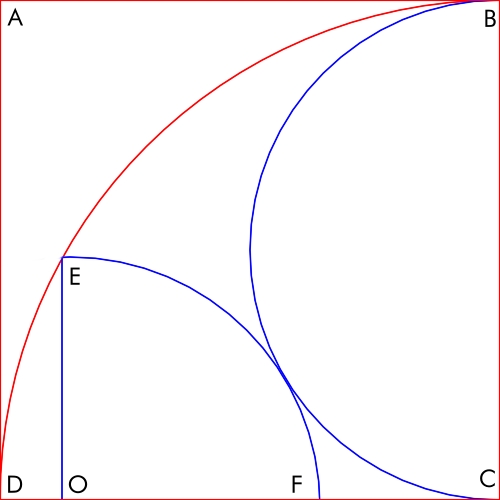
Mikä on OE:n pituus?
Tarkastellaan seuraavaa kaaviota.
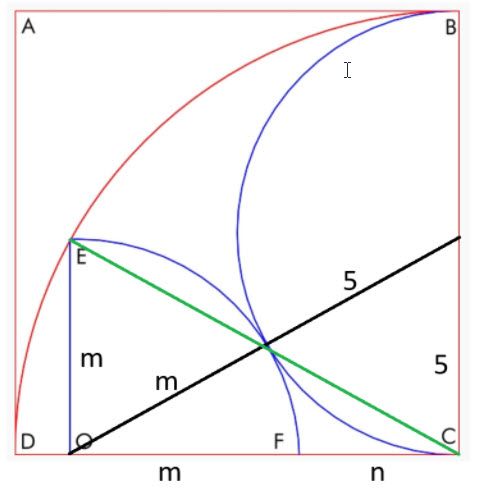
Tässä meillä on kaksi suorakulmaista kolmiota, toisen hypotenuusa on vihreä ja toisen musta. Muodostetaan kaksi Pythagoraan yhtälöä:
- Vihreä hypotenuusa: m² + (m+n) ² = 10²
- musta hypotenuusa: 5 2 + (m+n) 2 = (m+5) 2
Järjestetään ensimmäinen yhtälö uudelleen muotoon (m+n) ² = 10² - m²
Sijoitetaan tuo arvo (m+n) ₂: lle toiseen yhtälöön:
5 2 + 10 2 - m 2 = (m + 5) 2
25 + 100 - m² = m² + 10 m² + 25
2m² + 10m - 100 = 0
m² + 5m - 50 = 0
Ratkaise m Pythagoraan kaavan avulla:
m = (-5 +/- neliöjuuri(25 + 200))/2
m = 5 tai -10. 5 on ainoa järkevä vastaus.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Suuri määrä opiskelijoita suorittaa 10 kysymyksen testiä. Jokainen kysymys on oikein tai väärin. Mikä on enimmäismäärä opiskelijoita, jotka voivat suorittaa testin siten, että mitkä tahansa kaksi testiä eroavat toisistaan vähintään kahden kysymyksen verran?
Tee yksi testi, jota kutsumme avaintestiksi.
Ryhmä 1 = Niiden tapoja, joilla muut testit voivat poiketa avaintestistä tasan kahden kysymyksen verran, on combin(10,2)=45.
En aio laskea, kuinka monta tapaa eroaa avaintestistä kolmella, koska jotkut näistä tavoista vastaavat 9/10 ryhmän 1 testiä.
Ryhmä 2 = Muiden testien eroavaisuuksien lukumäärä avaintestistä täsmälleen neljällä kysymyksellä on combin(10,4)=210. Mikä tahansa näistä eroaa myös mistä tahansa ryhmän 1 testistä vähintään kahdella.
Toistetaanpa tätä logiikkaa...
- Ryhmä 3 = Niiden tapoja, joilla muut testit voivat poiketa avaintestistä tasan 6 kysymyksen verran, on combin(10,6)=210.
- Ryhmä 4 = Muiden testien ja avaintestin yhdistelmän määrä, joka on tasan 8 kysymystä, voi olla 45.
- Ryhmä 5 = Niiden tapoja, joilla muut testit voivat poiketa avaintestistä tasan 10 kysymyksen verran, on combin(10,10)=1.
Joten vastaus on ryhmien 1–5 summa plus yksi avaintestissä = 1 + 45 + 210 + 210 + 45 + 1 = 512.
Tuo luku on sama kuin 2^9. Voisiko se olla sattumaa? Ei!
Parittoman määrän alkioita voidaan nostaa suuremmasta ryhmästä yhtä monella eri tavalla kuin parillinen luku. Tämä johtuu siitä, että jokainen suuren ryhmän alkio voidaan joko valita tai jättää valitsematta. n alkion ryhmässä on 2^n yhdistelmää kutakin valittua tai valitsematta jäänyttä jäsentä. Jos ne lueteltaisiin systemaattisesti binäärijärjestyksessä, valittujen yhdistelmien lukumäärä vaihtelisi parillisen ja parittoman välillä. Ryhmän kokonaisluku on 2^n, joka itse on parillinen, joten puolet luvusta 2^n on parillinen.
Ryhmien 1–5 summa on siis niiden tapojen lukumäärä, joilla voidaan valita parillinen määrä kysymyksiä, jotka vastaavat avaintestiä. Tämä on yhtä suuri kuin niiden tapojen lukumäärä, joilla voidaan valita pariton määrä kysymyksiä, jotka vastaavat avaintestiä. Avaintestin täsmäämis- tai ei-täsmäämismahdollisuuksien kokonaismäärä on 2^10 = 10²⁻². Puolet näistä osuu parillisen määrän kertoja. Joten vastaus on 10²⁻² = 5¹²⁻².
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .


