Crapsit - Nopat ja heittäminen
Mietin, miten craps-pelissä voi muuttaa noppien lukua niin, että se osuu joka kerta lukuun 7 tai 11. Voitteko auttaa? Kiitos.
Muuta sitten niin, että toisessa nopassa on joka puolella kuutonen ja toisessa pelkkiä ykkösiä ja viitosia.
Uskotko, että pelaajien "toiveajattelu" voi vaikuttaa pelin lopputulokseen? Huomaa, etten ole kiinnostunut vaikutuksen KOKONAISUUDESTA, vain filosofisesta mielipiteestäsi. Uskotko myös, että tapa, jolla pelaaja heittää noppaa crapsissa, voi aiheuttaa vinouman (hyvän tai huonon) lopputulokseen? Kuten aina, sivustosi on MAHTAVA.
Kiitos ystävällisistä sanoista. En usko, että toiveajattelu auttaa kasinolla, jos kaikki muu pysyy samana.
Nopan vaikutusta koskeva kysymys on kuuma keskustelunaihe. Henkilökohtaisesti olen hyvin skeptinen. Tarkastellessani tätä vastausta vuonna 2013 en ole vieläkään nähnyt vakuuttavia todisteita siitä, että kukaan voisi vaikuttaa riittävästi saadakseen etua.
Haluaisin vain tietää mielipiteesi crapsin frekvenssitaulukon muuttamisesta noppien ennalta asettamalla ne.
Suhtaudun siihen hyvin skeptisesti. Käyn läpi joitakin aiheeseen liittyviä kokeita craps-liitteessäni 3 .
Opin hiljattain tietoa nopanheittostrategioista crapsissa. Jotkut uskovat, että nopat voi heittää tietyllä tavalla ennen heittoa, ja pitämällä nopanheiton vain yhdellä pyörimisakselilla voi saada vähemmän mahdollisia seiskoja tietyillä noppasetillä. Halusin tietää, onko tässä mitään perää vai onko se vain harhaluulo.
En usko siihen. Tähän mennessä en ole nähnyt nimeä, jota arvostan ja joka tukisi menetelmää, enkä mitään todisteita sen toimivuudesta. Vaikka en täysin sulje pois tätä mahdollisuutta, suhtaudun siihen erittäin skeptisesti. Asun ehkä Nevadassa, mutta kun on kyse esimerkiksi nopanheitosta, olen kotoisin Missourista. "Näytä minulle", että se toimii.
Ovatko nopat todella puolueettomia? Vaikuttaa siltä, että ne sivut, joissa on suurempia numeroita ja enemmän reikiä, olisivat kevyempiä kuin ne sivut, joissa on pienempiä numeroita ja vähemmän reikiä. Tämä viittaa siihen, että painavammat sivut todennäköisemmin osuvat kuvapuoli alaspäin ja suuremmat numerot todennäköisemmin kuvapuoli ylöspäin. Voin kuvitella craps-järjestelmän, joka voisi yrittää hyödyntää tätä periaatetta, mutta mietin, toimisiko se todella. Mitä mieltä olet?
Tavallisilla nopilla, kuten lautapeleissä, tämä pitää paikkansa. Kasinonopeissa on kuitenkin upotettuja täpliä. Tehtaalla porataan reikiä täpliä varten ja sitten reikiin työnnetään valkoisia täpliä, joiden tiheys on sama kuin itse nopan. Noppa on siis pohjimmiltaan täydellinen kuutio. Vaikka he käyttäisivätkin tavallisia lautapelin noppia, epäilen, että vinouma olisi läheskään riittävä kaventamaan talon etua.
Uskotko, että nopanheitto Casino Craps -pöydässä on todella sattumanvaraista, kuten satunnaislukugeneraattorissa (RNG), vai onko olemassa hyviä ja huonoja heittäjiä joko nopan "mekaniikan" tai huolimattoman heiton (esimerkiksi lyhyiden heittojen) kautta? Jos oikean maailman Casino Craps ei ole todella sattumanvaraista, miten voisin hyödyntää tätä?
Mielestäni ei ole olemassa luonnostaan huonoa heittäjää. Muutamaa ammattilaista lukuun ottamatta kaikkia nopanheittoja voidaan pitää todella satunnaisina. On seminaareja siitä, miten talon etu voi voittaa crapsissa prekessioheitolla, mutta en esitä väitteitä niiden puolesta tai niitä vastaan. En ole vielä nähnyt tarpeeksi todisteita kumpaankaan suuntaan.
Casino Player -lehden lokakuun numerossa Frank Scoblete kirjoitti artikkelin hallitusta nopanheitosta, jossa todetaan hävinneensä 1800 dollaria Stanford Wongille, kun tämä heitti vain 74 seiskaa 500 heitolla. Miksi lyötiin vetoa niin pienestä otoksesta (500)? Henkilön, joka väittää pystyvänsä hallitsemaan noppien heittoa, tulisi olla valmis osoittamaan taitonsa vähintään 50 000 heitolla. Olenko väärässä, jos ajattelen, että 500 heittoa on niin pieni otos, että melkein mitä tahansa voi tapahtua?
Hävisin 1800 dollaria toiselle uhkapelialan kirjoittajalle, en Stanfordille. Olisin mieluummin heittänyt enemmän, mutta aika oli selvä. Olettaen, että noppia heitettiin yksi minuutissa, 50 000 heiton suorittamiseen kuluisi 34,7 päivää. En ollut se, joka päätti 500 heitosta, mutta se vaikutti kohtuulliselta kompromissilta suuren otoskoon ja ajan välillä. Olet oikeassa siinä, että 500 on liian vähän perusteluja nopanheiton vaikuttamisen puolesta tai sitä vastaan, mutta 500 heittoa on parempi kuin nolla.
Tiedän, että olet skeptinen nopanheiton suhteen. Olen harjoitellut nopanheittoa ja hallittua heittoa kolme kuukautta. Mikä on todennäköisyys heittää 78 seiskaa 655 satunnaisella heitolla? Kiitos avusta :)
Suurille heittomäärille voimme käyttää Gaussin käyrän approksimaatiota. Odotusarvo seiskojen määrälle 655 heitolla on 655 × (1/6) = 109,1667. Varianssi on 655 × (1/6) × (5/6) = 90,9722. Keskihajonta on sqr(90,9722) = 9,5379. Saat 78 seiskaa 109,1667 − 78 = 31,1667 vähemmän kuin odotusarvo. Tämä on (31,1667 - 0,5) / 9,5379 = 3,22 keskihajontaa odotusarvoa pienemmäksi. Todennäköisyys sille, että jäädään 3,22 tai enemmän keskihajontaa odotusarvoa etelämmäksi, on 0,000641 eli 1/1 560. Sain tämän luvun Excelissä käyttämällä kaavaa normsdist(-3,22).
Tämä koskee nopanheiton hallintaa Craps-pelissä. Keskustelit aiemmin Stanford Wongin kokeesta ja totesit: "Vedonlyöntiehdot olivat, pystyisivätkö tarkkuusheittäjät heittämään alle 79,5 seiskaa 500 nopanheitolla. Satunnaispelissä odotettu luku olisi 83,33. Todennäköisyys saada 79 tai vähemmän seiskaa 500 satunnaisella heitolla on 32,66 %.... Todennäköisyys saada 74 tai vähemmän seiskaa 500 satunnaisella heitolla on 14,41 %."
Kysymykseni tästä vedosta on, että 14,41 % ei vieläkään ole "tilastollisesti merkitsevä" [eli p < 0,05], jolla yleensä tarkoitetaan suurempaa kuin kahta keskiarvosta mitattua keskihajontaa – tai todennäköisyyttä, että tapahtuma tapahtuu satunnaisesti alle 5 % sarjan *yhteensä* jommassakummassa päässä.
Kuinka monta seiskaa pitäisi heittää 500 heitolla, ennen kuin voitaisiin sanoa, että on alle 2,5 %:n todennäköisyys sille, että tulos oli täysin satunnainen (eli että tulos oli tilastollisesti merkitsevä)?
Paljon kiitoksia & muuten, sinun sivustosi on EHDOTTOMASTI PARAS löytämäni uhkapelikertoimiin ja -todennäköisyyksiin keskittyvä verkkosivusto... jatkakaa hyvää työtä!!!
Kiitos ystävällisistä sanoistasi. Sinun ei pitäisi sanoa, että todennäköisyys sille, että heitot eivät olleet satunnaisia, on p. Oikeammin se pitäisi muotoilla niin, että todennäköisyys sille, että satunnainen peli tuottaa tällaisen tuloksen, on p. Kukaan ei odottanut 500 heiton todistavan tai kumoavan mitään. En minä asettanut rajaa 79,5 seiskaan, mutta epäilen, että se valittiin tilastollisesti merkitseväksi; pikemminkin epäilen, että se oli piste, jossa molemmat osapuolet suostuivat vetoon.
2,5 %:n merkitsevyystaso on 1,96 keskihajontaa odotuksesta. Tämä voidaan löytää Excelissä kaavalla =normsinv(0,025). 500 heiton keskihajonta on sqr(500*(1/6)*(5/6)) = 8,333. Joten 1,96 keskihajontaa on 1,96 * 8,333 = 16,333 heittoa odotuksesta etelään. Odotettu seiskojen määrä 500 heitolla on 500*(1/6) = 83,333. Joten 1,96 keskihajontaa tästä etelään on 83,333 − 16,333 = 67. Binomijakaumalla tarkistetaan, että 67 seiskan tai vähemmän todennäköisyys on 2,627 %.
Kolme vuotta sitten kirjoitit Ask The Wizard -kolumnissa : "Olet oikeassa siinä, että 500 on liian vähän perusteluja nopanheiton vaikuttamisen puolesta tai sitä vastaan, mutta 500 heittoa on parempi kuin nolla." Voitko kuvailla, mitä vaadittaisit väitetyltä nopanheiton vaikuttajalta kokeessa, jotta tuntisit olosi tarpeeksi varmaksi alkaaksesi panostaa merkittäviä summia hänen puolestaan? Kysyn, koska miljardi kierrosta on hyvä vertailukohta "luotettaville" tuloksille joissakin blackjack-simulaatioissa. Tehokkaimmalla (eli vähiten heittoja vaativalla) kokeellisella suunnittelulla, jonka voit kuvitella, kuinka monta heittoa heittäjän pitäisi tehdä voidakseen olla varma, että hän vaikuttaa tuloksiin? Tiedän, että vastaus riippuu heittäjän taidoista, mutta ymmärrät pointtini. Jos tarvitset miljoona heittoa edes parhaassa tapauksessa, se ei ole kannattava yritys.
Ei ole olemassa mitään yksiselitteistä pistettä, jossa luottamus ansaitaan. Kyse on asteesta. Ensinnäkin kysyisin, mitä testataan ja mitä ampuja arvioi tapahtuvan. Kaikissa testeissä on kaksi mahdollista virhettä. Taitava ampuja saattaa epäonnistua huonon onnen vuoksi tai satunnainen ampuja voi läpäistä hyvän onnen vuoksi. Näistä kahdesta haluaisin välttää väärän positiivisen. Mielestäni kohtuullinen testi asettaisi väärän negatiivisen todennäköisyyden noin 5 prosenttiin ja väärän positiivisen noin 1 prosenttiin.
Oletetaan esimerkiksi, että väitteen esittäjä sanoo saavansa keskimäärin yhden seitsemän nopanheiton välein. Satunnainen heittäjä heittäisi keskimäärin yhden seiskan kuuden heiton välein. Yrityksen ja erehdyksen kautta olen havainnut, että molemmat kriteerit täyttävä testi olisi nopanheitto 3 600 kertaa, ja läpäisyyn vaadittaisiin 547 tai vähemmän seiskaa eli yksi seiska 6,58 heittoa kohden.
Joka seitsemän ampujan tulisi saada keskimäärin 514,3 seiskaa, keskihajonnan ollessa 21,00. Gaussin approksimaatiota käyttäen todennäköisyys sille, että tällainen taitava ampuja heittää 548 tai enemmän seiskaa (väärä negatiivinen), on 5,7 %. Satunnaisen ampujan tulisi saada keskimäärin 600 seiskaa, keskihajonnan ollessa 22,36. Satunnaisen ampujan testin läpäisyn todennäköisyys (väärä positiivinen) on 0,94 %. Alla oleva kaavio näyttää mahdolliset tulokset taitaville ja satunnaisille ampujille. Jos tulokset ovat vihreän viivan vasemmalla puolella, katsoisin ampujan läpäisseen testin ja lyöisin vetoa hänen puolestaan.
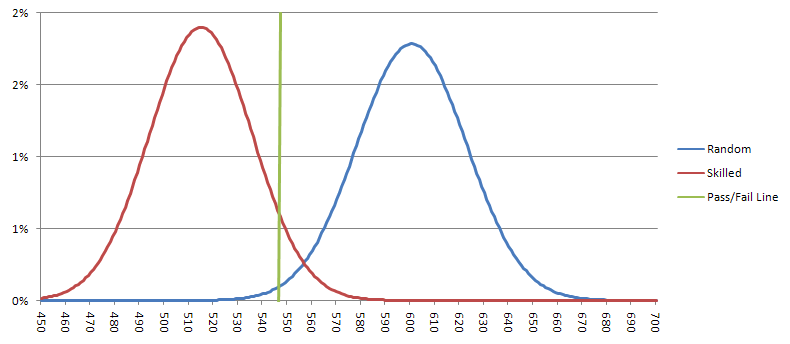
Käytännön dilemma on, että jos oletamme kaksi heittoa minuutissa, testin suorittamiseen kuluisi 30 tuntia. Ehkä voisin olla merkitsevyystason suhteen liberaalimpi ja lyhentää aikavaatimusta, mutta tulokset eivät olisi yhtä vakuuttavia. Mielestäni on tullut aika suuremmalle testille kuin 500 heiton Wong-kokeilulle.
Tänään uutisissa Atlantic Cityssä asuva nainen heitti 154 kertaa peräkkäin ennen kuin sai seitsemän Borgatassa . Tämä tarkoittaa, että hän heitti kahta noppaa 154 kertaa, eikä yhtään seiskaa tullut. Joten otin (30/36) 154 ja sain kertoimeksi yli 1,5 biljoonaa yhteen. On noin 9 000 kertaa todennäköisempää voittaa Mega Millions -lotossa kuin heittää maratonin, jossa ei ole seitsemää noppaa. Ottaen huomioon, kuinka tähtitieteellisen epätodennäköistä tämä on, ja ottaen huomioon, että ihmiset tuomitaan DNA-todisteiden perusteella, jotka ovat miljardeja yhteen vastaan väärää osumaa, kuinka paljon epäilisit huijaamista ja tarjoaisitko konsultoida Borgataa tästä? Soitin heille jo, annoin nimeni ja käskin heidän tehdä sillä mitä haluavat. Olen utelias ajatuksistasi.
Ensinnäkin, hän heitti noppaa yhteensä 154 kertaa, ja 154. heitto oli seitsemän ulos ( Lähde: NJ.com ). Tämä ei kuitenkaan tarkoita, etteikö hän olisi koskaan heittänyt seiskaa ensimmäisten 153 heiton aikana. Hän olisi voinut heittää niitä paljon come out -heitoilla. Kuten osoitan 3. toukokuuta 2003 julkaisemassani kolumnissa , todennäköisyys päästä 154. heittoon on 1/5,6 miljardia. Mega Millionsin voittotodennäköisyys on 1 yhdistelmässä (56,5)*46 = 175 711 536. Joten 154 tai useamman heiton saavuttaminen on noin 32 kertaa vaikeampaa. Jos aikaa ja pöytiä on riittävästi, joita uskon olevan olemassa, jotain tällaista tapahtuisi väistämättä ennemmin tai myöhemmin. Joten en epäilisi huijaamista. Arvioin karkeasti noin 1 prosentin todennäköisyydeksi sille, että näin tapahtuu minä tahansa vuonna.
Katso myös ratkaisuni, matriiseilla ilmaistuna, osoitteessa mathproblems.info , tehtävä 204.
Mielestäni jotkut Las Vegasin kasinot käyttävät noppia, joissa painotus on toiselta puolelta. Todisteena esitän 244 heiton tulokset, jotka keräsin Stripin kasinolla. Millä todennäköisyydellä näin vääristyneet tulokset voisivat tulla reiluista nopista?
| Nopan testitiedot | |
| Noppien kokonaismäärä | Havainnot |
| 2 | 6 |
| 3 | 12 |
| 4 | 14 |
| 5 | 18 |
| 6 | 23 |
| 7 | 50 |
| 8 | 36 |
| 9 | 37 |
| 10 | 27 |
| 11 | 14 |
| 12 | 7 |
| Kokonais | 244 |
7,7 %.
Khiin neliö -testi sopii täydellisesti tällaiseen kysymykseen. Testiä käytetään ottamalla (ae) 2 /e kullekin kategorialle, jossa a on todellinen tulos ja e on odotettu tulos. Esimerkiksi odotettu 2:n heittojen lukumäärä 244 heitolla on 244 × (1/36) = 6,777778. Jos et ymmärrä, miksi 2:n heiton todennäköisyys on 1/36, lue sivuni nopan todennäköisyyden perusteista . Khiin neliön arvon saamiseksi kokonaisluvulle 2 a=6 ja e=6,777778, joten (ae) 2 /e = (6 - 6,777778) 2 /6,777778 = 0,089253802.
Khiin neliön tulokset
| Noppien kokonaismäärä | Havainnot | Odotettu | Khiin neliö |
| 2 | 6 | 6.777778 | 0,089253 |
| 3 | 12 | 13.555556 | 0,178506 |
| 4 | 14 | 20.333333 | 1.972678 |
| 5 | 18 | 27.111111 | 3.061931 |
| 6 | 23 | 33.888889 | 3.498725 |
| 7 | 50 | 40.666667 | 2.142077 |
| 8 | 36 | 33.888889 | 0.131512 |
| 9 | 37 | 27.111111 | 3.607013 |
| 10 | 27 | 20.333333 | 2.185792 |
| 11 | 14 | 13.555556 | 0,014572 |
| 12 | 7 | 6.777778 | 0,007286 |
| Kokonais | 244 | 244 | 16.889344 |
Laske sitten khiin neliö -sarakkeen summa. Tässä esimerkissä summa on 16,889344. Tätä kutsutaan khiin neliö -tilastoksi. "Vapausasteiden" lukumäärä on yksi pienempi kuin datan luokkien lukumäärä, tässä tapauksessa 11 - 1 = 10. Lopuksi joko etsi tilastotaulukosta khiin neliö -tilasto 10,52 ja 10 vapausastetta tai käytä Excelissä kaavaa =chidist(16,889344,10). Kumpikin antaa tulokseksi 7,7 %. Tämä tarkoittaa, että todennäköisyys sille, että reilu noppa tuottaa näin tai enemmän vinoja tuloksia, on 7,7 %. Yhteenvetona voidaan todeta, että vaikka nämä tulokset ovat odotettua vinompia, ne eivät ole niin vinoja, että ne herättäisivät ihmetystä. Jos jatkat tätä testiä, ehdotan, että keräät kunkin nopan yksittäisen tuloksen summan sijaan. On myös huomattava, että khiin neliö -testi ei sovellu, jos luokkien odotettu tulosten lukumäärä on pieni. Vähimmäisodotusarvo 5 on yleisesti käytetty luku.
Mitä tapahtuisi, jos craps-pelissä kaksi noppaa osuisi päällekkäin? Olisiko kyseessä pätevä heitto? Jos olisi, miten jakaja paljastaisi, mille numerolle alempi noppa osui?
Se, onko heitto pätevä, riippuu sijainnistasi. New Jerseyn pelisäännöt 19:47-1.9(a) todetaan seuraavasti:
Nopanheitto on mitätön, jos jompikumpi tai molemmat nopat putoavat pöydältä tai jos toinen noppa pysähtyy toisen päälle. -- NJ 19:47-1.9(a)
Pennsylvaniassa on täsmälleen sama asetus, pykälä 537.9(a) :
Nopanheitto on mitätön, jos jompikumpi tai molemmat nopat putoavat pöydältä tai jos toinen noppa pysähtyy toisen päälle. -- PA 537.9(a)
Kysyin Las Vegasin noppajakajalta, joka sanoi, että siellä sitä kutsuttaisiin päteväksi heitoksi, jos se muuten olisi oikea heitto. Vaikka hän ei ole koskaan nähnyt niin tapahtuvan, hän sanoi, että jos niin kävisi, jakajat yksinkertaisesti siirtäisivät ylintä noppaa nähdäkseen, mille numerolle alempi noppa laskeutui. Alemman nopan tuloksen voi kuitenkin määrittää koskematta ylimpään noppaan tai katsomatta sen läpi. Näin se tehdään. Ensinnäkin, katsomalla neljää sivua voit rajata ylimmät mahdollisuudet kahteen. Näin se selviää kolmen mahdollisuuden mukaan.
- 1 tai 6: Etsi numeroa 3. Jos korkein piste on numeron 5 vieressä, numero 1 on päällimmäisenä. Muussa tapauksessa, jos se on numeron 2 vieressä, numero 6 on päällimmäisenä.
- 2 tai 5: Etsi numeroa 3. Jos korkein piste on luvun 6 vieressä, numero 2 on päällimmäisenä. Muussa tapauksessa, jos se on luvun 1 vieressä, numero 5 on päällimmäisenä.
- 3 tai 4: Etsi numeroa 2. Jos ylin piste on luvun 6 vieressä, numero 3 on päällimmäisenä. Muussa tapauksessa, jos se on luvun 1 vieressä, numero 4 on päällimmäisenä.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mikä on odotettavissa oleva kahden nopan heittojen määrä, jotka tapahtuvat ainakin kerran jokaisella kokonaisluvulla 2–12?
Tämä kysymys esitettiin TwoPlusTwo.com-sivustolla, ja BruceZ vastasi siihen oikein. Seuraava ratkaisu on sama kuin BruceZ:n menetelmä, josta hän ansaitsee ansaitsemansa tunnustuksen. Vastaus on vaikea, joten kiinnitä siihen huomiota.
Tarkastellaan ensin odotettua heittojen määrää, jotta saadaan yhteensä kaksi. Todennäköisyys kakkoselle on 1/36, joten kahden ensimmäisen saamiseksi tarvittaisiin keskimäärin 36 heittoa.
Tarkastellaan seuraavaksi odotettua heittojen määrää, jolla saadaan sekä kaksi että kolme. Tiedämme jo, että kahden tuloksen saavuttamiseen tarvitaan keskimäärin 36 heittoa. Jos kolmosen saa odottaessaan kahta, kolmosen saamiseksi ei tarvita lisäheittoja. Muussa tapauksessa noppaa on heitettävä enemmän, jotta saadaan kolmosen tulos.
Kolmosen todennäköisyys on 1/18, joten kolmosen saamiseen tarvittaisiin keskimäärin 18 lisäheittoa, jos kaksi heistä tulisi ensin. Koska kakkosen voi heittää vain yhdellä tavalla ja kolmosen voi heittää kahdella tavalla, todennäköisyys sille, että kaksi heistä heitetään ensin, on 1/(1+2) = 1/3.
Joten on 1/3 todennäköisyys, että tarvitsemme 18 ylimääräistä heittoa saadaksemme kolmosen. Näin ollen odotettu heittojen määrä sekä kakkosen että kolmosen saamiseksi on 36 + (1/3) × 18 = 42.
Seuraavaksi mieti, kuinka monta heittoa lisää tarvitset saadaksesi myös nelonen. Jos et vielä saanut nelosta, kun heität kakkosen ja kolmosen, sinun on heitettävä noppaa keskimäärin 12 kertaa lisää saadaksesi sellaisen. Tämä johtuu siitä, että nelosen todennäköisyys on 1/12.
Mikä on todennäköisyys saada neljä ennen kuin saavutetaan kaksi ja kolme? Tarkastellaan ensin yleistä todennäköisyyssääntöä tilanteisiin, joissa A ja B eivät ole toisensa poissulkevia:
pr(A tai B) = pr(A) + pr(B) - pr(A ja B)
Vähennät pr(A:n ja B:n), koska tämä kontingentti lasketaan kahdesti pr(A):ssa + pr(B):ssä. Joten,
pr(4 ennen 2 tai 3) = pr(4 ennen 2) + pr(4 ennen 3) - pr(4 ennen 2 ja 3) = (3/4) + (3/5) - (3/6) = 0,85.
Todennäköisyys sille, ettei nelosta saada matkalla lukuihin kaksi ja kolme, on 1,0 - 0,85 = 0,15. Joten on 15 %:n todennäköisyys sille, että tarvitaan 12 ylimääräistä heittoa. Näin ollen odotettu heittojen määrä lukujen kaksi, kolme ja nelon saamiseksi on 42 + 0,15 * 12 = 43,8.
Seuraavaksi mieti, kuinka monta heittoa lisää tarvitset saadaksesi myös viitonen. Siihen mennessä, kun heität kaksi neljään ja et vielä saanut viitosen, sinun on heitettävä noppaa keskimäärin 9 kertaa lisää saadaksesi sellaisen, koska viitosen todennäköisyys on 4/36 = 1/9.
Mikä on todennäköisyys saada viisi ennen kuin saavutetaan kaksi, kolme tai neljä? Yleinen sääntö on:
pr(A tai B tai C) = pr(A) + pr(B) + pr(C) - pr(A ja B) - pr(A ja C) - pr(B ja C) + pr(A ja B ja C)
Joten pr(5 ennen 2 tai 3 tai 4) = pr(5 ennen 2) + pr(5 ennen 3) + pr(5 ennen 4) - pr(5 ennen 2 ja 3) - pr(5 ennen 2 ja 4) - pr(5 ennen 3 ja 4) + pr(5 ennen 2, 3 ja 4) = (4/5) + (4/6) + (4/7) - (4/7) - (4/8) - (4/9) + (4/10) = 83/90. Todennäköisyys sille, ettei neljää saada matkalla kahdesta neljään, on 1 - 83/90 = 7/90. Joten on 7,78 %:n todennäköisyys tarvita 7,2 ylimääräistä heittoa. Näin ollen odotettu heittojen määrä tulosten kaksi, kolme, neljä ja viisi saamiseksi on 43,8 + (7/90) * 9 = 44,5.
Jatka samalla logiikalla, kunnes kokonaissumma on kuudesta kahteentoista. Laskutoimitusten määrä, joka tarvitaan seuraavan luvun saamisen todennäköisyyden laskemiseen ennen kuin viimeinen luku tarvitaan, kaksinkertaistuu joka kerta. Siihen mennessä, kun pääset kahteentoista, sinun on tehtävä 1 023 laskutoimitusta.
Tässä on yleinen sääntö pr(A tai B tai C tai ... tai Z) -funktiolle
pr(A tai B tai C tai ... tai Z) =
pr(A) + pr(B) + ... + pr(Z)
- pr(A ja B) - pr(A ja C) - ... - pr(Y ja Z) Vähennä jokaisen kahden tapahtuman yhdistelmän todennäköisyys
+ pr(A ja B ja C) + pr(A ja B ja D) + ... + pr(X ja Y ja Z) Laske yhteen jokaisen kolmen tapahtuman yhdistelmän todennäköisyys
- pr(A ja B ja C ja D) - pr(A ja B ja C ja E) - ... - pr(W ja X ja Y ja Z) Vähennä jokaisen neljän tapahtuman yhdistelmän todennäköisyysToista sitten uudelleen ja muista lisätä todennäköisyydet parittomille tapahtumille ja vähentää todennäköisyydet parillisille tapahtumille. Tämä on luonnollisesti työlästä suuren määrän mahdollisten tapahtumien kohdalla ja käytännössä vaatii taulukkolaskentaohjelman tai tietokoneohjelman.
Seuraava taulukko näyttää odotetun lukumäärän kullekin askeleelle matkan varrella. Esimerkiksi 36 antaa tulokseksi kaksi, 42 antaa tulokseksi kaksi ja sitten kolme. Oikeassa alakulmassa oleva solu näyttää odotetun heittojen lukumäärän kaikkien 11 tuloksen saamiseksi, joka on 61,217385.
Odotettu rullien lukumäärä -ongelma
| Suurin tarvittava numero | Todennäköisyys | Odotetut heitot tarvittaessa | Todennäköisyyttä ei tarvita | Tarvittava todennäköisyys | Odotettu heittojen kokonaismäärä |
|---|---|---|---|---|---|
| 2 | 0,027778 | 36,0 | 0.000000 | 1.000000 | 36.000000 |
| 3 | 0,055556 | 18.0 | 0,666667 | 0,333333 | 42.000000 |
| 4 | 0,083333 | 12.0 | 0,850000 | 0,150000 | 43.800000 |
| 5 | 0.111111 | 9.0 | 0,922222 | 0,077778 | 44,500000 |
| 6 | 0.138889 | 7.2 | 0,956044 | 0,043956 | 44.816484 |
| 7 | 0,166667 | 6.0 | 0,973646 | 0,026354 | 44.974607 |
| 8 | 0.138889 | 7.2 | 0,962994 | 0,037006 | 45.241049 |
| 9 | 0.111111 | 9.0 | 0,944827 | 0,055173 | 45.737607 |
| 10 | 0,083333 | 12.0 | 0,911570 | 0.088430 | 46.798765 |
| 11 | 0,055556 | 18.0 | 0,843824 | 0,156176 | 49.609939 |
| 12 | 0,027778 | 36,0 | 0,677571 | 0.322429 | 61.217385 |
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Velhon mukaan tuo verkkosivusto kuulostaa pelkältä höpinältä ja jaarittelulta ilman minkäänlaisia uskottavia todisteita syytösten tueksi. Paljastan mielelläni minkä tahansa kasinon puolueellisten noppien käytöstä, jos minulla olisi siitä todisteita.
Jos jollakulla on päteviä todisteita puolueellisista nopanheitoista, tutkisin ne mielelläni ja julkaisisin johtopäätökseni. Haluaisin nähdä joko lokitiedostoja heitoista tai, vielä parempi, joitain todellisia väitettyjä puolueellisia nopanheittoja.
Lisäksi, jos kasinot todella käyttivät noppaa, joka tuotti odotettua enemmän seiskoja, niin miksi nämä etsivät eivät ole tietoisia salaliitosta, jossa lyödään vetoa "don't pass" -tapauksesta ja asetetaan kertoimia?
Peliautomaattien Hot Roll -bonuskierros antaa pelaajalle seuraavan määrän kolikoita kahden nopan heittojen summan mukaan. Pelaaja jatkaa keräämistä, kunnes hän heittää yhteensä seitsemän, mikä päättää bonuspelin. Jos hän heittää ensimmäisellä heitolla seitsemän, hän saa lohdutuspalkinnon 70 kolikkoa. Seuraavat ovat palkinnot kaikille muille kokonaistuloksille paitsi seitsemälle:
- 2 tai 12: 1 000
- 3 tai 11: 600
- 4 tai 10: 400
- 5 tai 9: 300
- 6 tai 8: 200
Kysymykseni kuuluu, mikä on keskimääräinen bonusvoitto?
Napsauta seuraavaa painiketta nähdäksesi vastauksen.
Napsauta seuraavaa painiketta nähdäksesi ratkaisun.
[spoileri] Olkoon x vastaus. Niin kauan kuin pelaaja ei heitä seiskaa, hän voi aina odottaa tulevien voittojen olevan x kaikkien aiempien voittojen lisäksi. Toisin sanoen nopanheitossa on muistiton ominaisuus: riippumatta siitä, kuinka monta heittoa olet jo heittänyt, et ole lähempänä seiskaa kuin olit aloittaessasi.En aio käydä läpi nopanheiton todennäköisyyksien perusteita, vaan sanon vain, että kunkin kokonaissumman todennäköisyys on seuraava:
- 2: 1/36
- 3: 2/36
- 4: 3/36
- 5: 4/36
- 6: 5/36
- 7: 6/36
- 8:5/36
- 9: 4/36
- 10: 3/36
- 11: 2/36
- 12: 1/36
Ennen lohdutuspalkinnon tarkastelua x:n arvo voidaan ilmaista seuraavasti:
x = (1/36)*(1000 + x) + (2/36)*(600 + x) + (3/36)*(400 + x) + (4/36)*(300 + x) + (5/36)*(200 + x) + (5/36)*(200 + x) + (4/36)*(300 + x) + (3/36)*(400 + x) + (2/36)*(600 + x) + (1/36)*(1000 + x)Seuraavaksi kerro molemmat puolet 36:lla:
36x = (1000 + x) + 2*(600 + x) + 3*(400 + x) + 4*(300 + x) + 5*(200 + x) + 5*(200 + x) + 4*(300 + x) + 3*(400 + x) + 2*(600 + x) + (1000 + x)36x = 11 200 + 30x
6x = 11 200
x = 11 200/6 = 1866,67.
Seuraavaksi lohdutuspalkinnon arvo on 700 * (6/36) = 116,67.
Bonuksen keskimääräinen voitto on siis 1866,67 + 116,67 = 1983,33.
[/spoiler]


