Muut kuin kasinopelit - Usein kysytyt kysymykset
Tykkään pelata valehtelijapokeria dollariseteleillä. Mikä on todennäköisyys saada setelille 1, 2, 3, 4 tai 5 samaa numeroa? Kiitos. Jos pelaan kolmen hengen pelissä, mikä on todennäköisyys sille, että yksi numero ilmestyy?
Ensin vastaan esittämättömään kysymykseen todennäköisyydestä, että tietty luku esiintyy n kertaa satunnaisella setelillä. Setelissä on 8 numeroa, joten tietyn luvun n todennäköisyys on combin(8,n)* 0.1n * 0.98-n / 108 . Tässä on taulukko, joka näyttää tietyn luvun todennäköisyyden sille, että se esiintyy 0-8.
Tarkat numerokertoimet Liar's Pokerissa
| Määrä | Todennäköisyys |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Kokonais | 1.00000000 |
Seuraava taulukko näyttää kaikkien mahdollisten setelityyppien todennäköisyydet luokiteltuna kunkin n samanlaisen setelin lukumäärän mukaan. Esimerkiksi sarjanumerolla 66847680 olisi yksi kolmoset, yksi pari ja kolme yksittäistä seteliä, jolloin todennäköisyys olisi 0,1693440.
Yleiset todennäköisyydet valehtelijapokerissa
| 8 tammea | 7 tammea | 6 tammea | 5 tammea | 4 tammea | 3 tammea | 2 tammea | 1 tammi | Todennäköisyys |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0,0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0,0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0,3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Kokonais | 1.0000000 | |||||||
tammi = "eräänlainen"
Lisätietoja on valehtelijapokeria käsittelevällä sivullani.
Bank of America tarjoaa kolminkertaistaa yhden pankkiautomaatilla tehdyn talletuksen päivässä. Kilpailu kestää noin kaksi kuukautta. Ovatko todennäköisyyteni paremmat, kun talletan 300 dollaria... ja teen kolme 100 dollarin tai yhden 300 dollarin talletuksen... vai ovatko todennäköisyyteni niin pienet, ettei ero ole vaivan arvoinen?
Odotettu voittosi on sama riippumatta siitä, kuinka monta kertaa jaat talletuksesi kokonaisuudessaan. Hyvä strategia olisi tallettaa ja nostaa sama raha yhä uudelleen ja uudelleen niin monta kertaa kuin mahdollista. Todennäköisyytesi voivat kuitenkin olla niin huonot, ettei se ole vaivan arvoista.
Vain kysymys itämaisesta noppapelistä, jossa pelaajien on arvattava, kumpi puoli nopasta tulee näkyviin. Pelaajat asettavat ensin panoksensa numeroille 1, 2, 3, 4, 5 ja 6 (kuten ruletissa) ja sitten "jakaja" heittää samanaikaisesti kolmea noppaa. Voitot ovat 1:1, jos valittu numero ilmestyy kerran (millä tahansa kolmesta nopasta), 2:1, jos valittu numero ilmestyy kahdesti, ja 3:1, jos valittu numero ilmestyy kaikille kolmelle nopalle. Koska pelaaja voi asettaa minkä tahansa määrän panoksia laudalla, mikä on optimaalinen panosten määrä? (olettaen, että kaikki panokseni ovat samansuuruisia)
Kolmen samanlaisen tuloksen todennäköisyys on 1/216. Kahden samanlaisen tuloksen todennäköisyys on 3 * 5/216. Yhden samanlaisen tuloksen todennäköisyys on 25 * 5/216. Yhden samanlaisen tuloksen todennäköisyys on 5 * 5 * 5/216. Joten odotettu tuotto on 3 * (1/216) + 2 * (15/216) + 1 * (75/216) - 1 * (125/216) = - 17/216 = - 7,87 %. Optimaalista vetojen määrää ei ole, joten menetät odotetusti 7,87 % panoksestasi riippumatta siitä, mitä teet.
Näitä vetoja voi tehdä sekä Sic Bossa että Chuck a Luckissa .
Mitkä ovat todennäköisyydet voittaa Klondike-pasianssin normaalissa pelissä Windows-versiossa?
Tuo on luultavasti useimmin kysytty kysymys, johon minulla ei ole vastausta. Kattavaa Klondike-pasianssia ei ole koskaan pelattu. Ehkä joku lopulta tekee sen, kun tietokoneet ovat miljoona kertaa nopeampia. Huhutaan kuitenkin, että Vegasin kasinot tarjosivat peliä ainakin 1950-luvulla. Olen pyytänyt useita Vegasin vanhoja pelaajia vahvistamaan tämän, mutta kukaan ei ole vielä pystynyt siihen.
Heitin hiljattain backgammonia pelatessani neljä kertaa peräkkäin tuplana kuutoset. Mikä on todennäköisyys, että tämä tapahtuu uudelleen?
Jokaisella uudella heitolla todennäköisyys, että seuraavat neljä heittoa ovat kaikki tuplana kuutosia, on (1/36) 4 = 1/1679616.
Hei, osoitteessa www.transience.com.au/pearl.html on peli nimeltä Helmet sioille. Helmet on ryhmitelty kolmeen riviin (5+4+3), ja vuorollasi voit poistaa niin monta helmeä kuin haluat yhdeltä riviltä. Pelin tavoitteena on jättää viimeiset helmet vastustajasi otettavaksi. Pelaaja (minä) aloittaa aina (ja aina häviää). Miksi en koskaan voita? Vastustajallani on ovela järjestelmä voittaa aina, voitko paljastaa hänen salaisuutensa?
Aloita poistamalla kaksi helmeä riviltä, jossa on kolme helmeä, jolloin jäljelle jää 1 + 4 + 5. Riippumatta siitä, mitä vastustajasi tekee seuraavalla vuorollasi, jätä hänelle jokin seuraavista: 1 + 1 + 1, 1 + 2 + 3 tai 4 + 4. Mikä tahansa näistä pakottaa vastustajan tilanteeseen, jossa on kaksi vähintään kahden helmen pinoa tai pariton määrä yhden helmen pinoja.
Mikä monopolisetti on paras?
Pidän eniten oranssista setistä. Se tarjoaa parhaan sijoitetun pääoman tuoton. Esimerkiksi hotelli maksaa oranssissa setissä 500 dollaria ja keskimääräinen vuokra on 966,67 dollaria, jolloin vuokra-kulusuhde on 1,93. Ainoa setti, jossa suhde on korkeampi, on vaaleansininen setti, jossa se on 2,27. Vaaleansinisten settien enimmäisvuokra on kuitenkin vain 600 dollaria. Kolmen talon vuokrat oranssissa setissä ovat samat kuin vaaleansinisissä setissä olevien hotellien vuokrat, mutta ne ovat 20 % halvempia, ja tilaa on rakentaa lisää. Lisäksi oranssit setit ovat kypsiä juuri vankilasta tulleille. Joten ota neuvostani vaarin ja yritä kaupankäynnissä saada oranssi setti.
Mitä vinkkejä antaisit kivi-paperi-saksileikkiin?
Paras neuvo tällä sivustolla saattaa olla tämä: Ensimmäisellä kierroksella VALITSE AINA PAPERI. Tämä johtuu siitä, että amatööripelaajat valitsevat yleensä kiven ensimmäisellä kerralla. Ojenna vain kätesi jokaiseen asentoon yksi kerrallaan, ja huomaat, että kivi on mukavin ja luonnollisin valinta. Jos pelaat toistuvia kierroksia, sinun tulisi valita se, mikä voittaisi vastustajasi viimeisellä kierroksella alle kolmanneksen todennäköisyydellä. Tämä johtuu siitä, että uskon, että amatöörit toistavat alle kolmanneksen ajasta. Jos pelaat ammattilaista vastaan, jonka pelkäät pääsevän päähäsi, valitse satunnaisesti katsomalla kellosi sekuntiviisaria, jaa sekuntien määrä kolmella ja ota jakojäännös, ja sijoita sitten jäljellä oleva pelaaja seuraavasti: 0 = kivi, 1 = sakset, 2 = paperi (tai mikä tahansa muu etukäteen määritelty sijoittelu). Joten seuraavan kerran, kun menet ravintolaan hollantilaiseen tyyliin, ehdotan, että pelaat yhden kierroksen shakkia varten ja valitset sitten paperin. Voit kiittää minua myöhemmin.
Kenellä on etulyöntiasema riskin suhteen, kun hyökkääjä heittää kolme noppaa ja puolustaja kaksi?
Niille, jotka eivät tunne peliä, Risk on kaikkien aikojen paras lautapeli. Ne, jotka eivät ole pelanneet, eivät ole vielä eläneet. Vastauksena kysymykseesi yleisessä 3 vs 2 -taistelussa, seuraavat mahdolliset lopputulokset:
- Puolustaja häviää molemmat: 37,17 %
- Jokainen menettää yhden: 33,58 %
- Hyökkääjä häviää molemmat: 29,26 %
Mikä on todennäköisyys saada Yahtzee-pelissä onnistua, jos kortille jää vain Yahtzee?
Seuraava taulukko näyttää viimeisen heiton onnistumisen todennäköisyyden riippuen siitä, kuinka monta lisänoppaheittoa tarvitset Yahtzeen muodostamiseen.
Viimeisen heiton Yahtzee-todennäköisyydet
| Tarvitaan | Todennäköisyys menestyksestä |
| 0 | 1 |
| 1 | 0,166667 |
| 2 | 0,027778 |
| 3 | 0,00463 |
| 4 | 0,000772 |
Seuraava taulukko näyttää parannuksen todennäköisyydet. Vasen sarake näyttää, kuinka monta noppaa tarvitset ennen tiettyä heittoa, ja ylin sarake näyttää, kuinka monta tarvitset heiton jälkeen. Taulukon runko näyttää annetun parannusasteen todennäköisyyden.
Parantumisen todennäköisyydet
| Tarve ennen rullaamista | 0 | 1 | 2 | 3 | 4 | Kokonais |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0,166667 | 0,833333 | 0 | 0 | 0 | 1 |
| 2 | 0,027778 | 0,277778 | 0.694444 | 0 | 0 | 1 |
| 3 | 0,00463 | 0,069444 | 0,37037 | 0,555556 | 0 | 1 |
| 4 | 0,000772 | 0,01929 | 0.192901 | 0.694444 | 0,092593 | 1 |
Seuraava taulukko näyttää todennäköisyyden sille, että ensimmäisellä heitolla tarvitaan 0–4 noppaa lisää Yahtzeen muodostamiseen.
Ensimmäisen heiton Yahtzee-todennäköisyydet
| Tarvitaan | Todennäköisyys |
| 0 | 0,000772 |
| 1 | 0,019290 |
| 2 | 0.192901 |
| 3 | 0.694444 |
| 4 | 0,092593 |
Seuraava taulukko näyttää parannuksen ja sitten lopullisen onnistumisen todennäköisyyden ensimmäisen heiton jälkeen tarvittavan numeron mukaan. Esimerkiksi, jos pelaaja tarvitsee 3 noppaa lisää Yahtzeen muodostamiseen, todennäköisyys sille, että parannus tarvitaan 2 noppaa lisää toisen heiton jälkeen ja Yahtzee onnistuu kolmannella heitolla, on 0,010288066.
Yahtzeen todennäköisyydet ensimmäisen heiton jälkeen toisen heiton jälkeen tarvittavien numeroiden mukaan
| Tarve ennen rullaamista | 0 | 1 | 2 | 3 | 4 | Kokonais |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0,166667 | 0.138889 | 0 | 0 | 0 | 0.305556 |
| 2 | 0,027778 | 0,046296 | 0,01929 | 0 | 0 | 0,093364 |
| 3 | 0,00463 | 0,011574 | 0,010288 | 0,002572 | 0 | 0,029064 |
| 4 | 0,000772 | 0,003215 | 0,005358 | 0,003215 | 0,000071 | 0,012631 |
Lopullisen vastauksen saamiseksi lasketaan kahden taulukon päässä olevan ensimmäisen heiton jälkeen tarvittavan luvun pistetulo ja yhden taulukon päässä olevan viimeisen sarakkeen mahdollisen onnistumisen todennäköisyys. Tämä on 0,092593 * 0,012631 + 0,694444 * 0,029064 + 0,192901 * 0,093364 + 0,019290 * 0,305556 + 0,000772 * 1 = 4,6028643%. Vahvistaakseni tämän tein 100 000 000 pelisimulaation, ja simuloitu todennäköisyys oli 4,60562%.
Jos dynamiitti otetaan käyttöön vaihtoehtona kivi/paperi/sakset-pelissä, jossa dynamiitti voittaa kiven ja paperin, mutta sakset dynamiittia, mikä olisi optimaalinen strategia, jos pelaa kaksi täydellistä loogikkoa?
Ensinnäkin voimme sulkea pois paperilla pelaamisen. Riippumatta siitä, mitä toinen henkilö heittää, tulet tasavertaiseksi tai paremmaksi heittämällä dynamiittia paperin päälle. Kun paperi on pudonnut, dynamiitista tulee käytännössä uusi paperi, joka voittaa kiven ja häviää saksille. Täydellinen strategia on siis valita satunnaisesti ja yhtä todennäköisesti kiven, saksien ja dynamiittien välillä.
Mikä on paras strategia sellaisessa kojussa, jossa rahat lentelevät ympäriinsä ja sinun on kerättävä mahdollisimman paljon rajoitetussa ajassa?
Kysyin tämän kysymyksen Randy Hilliltä Fun Industries Inc: stä. Hän sanoi, että sinun pitäisi pitää kätesi suorina, kämmenet alaspäin, ja antaa rahojen räjähtää käsiesi ja käsivartesi pohjaa vasten. Kun rahaa on kertynyt tarpeeksi, työnnä se aukon läpi.
Oletetaan, että meillä on uhkapeli. Heitetään toistuvasti puolueetonta kolikkoa. Jokaisella heitolla on maksettava 1 rupia. Mahdollisia tuloksia on kaksi: H tai T. Jos heitettyjen kolikoiden ja häntäkolikoiden välinen erotus on 3, saamme pelaajalta 8 rupiaa. Pitäisikö meidän pelata peliä ja miksi? Kuinka suuri on voittotodennäköisyytemme? Miten voittotodennäköisyyteen pitäisi vaikuttaa, jos saamme 7 tai 9 rupiaa?
Kutsutaan x:ää odotetuksi volttien lukumääräksi lähtöpisteestä.
Kutsutaan y:tä jäljellä olevien volttien odotetuksi lukumääräksi, jos toinen puoli on enemmistönä yksi voltti.
Kutsutaan z:tä jäljellä olevien volttien odotetuksi lukumääräksi, jos toisella puolella on enemmistönä kaksi volttia.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5 * E(y)
Matriisialgebralla on helppo nähdä, että E(x) = 9, E(y) = 8 ja E(z) = 5. Keskimäärin tarvitaan 9 heittoa, jotta kruunan ja klaavan välinen ero on 3. Joten 8 rupian panoksella se on hyvä veto sille, joka saa yhden rupian heittoa kohden, koska hän saa keskimäärin 9 rupiaa, mutta maksaa takaisin vain 8. Talon etu pelaajalle on 11,11 %. 9 rupian panoksella se on reilu veto, 7 rupian panoksella talon etu on 22,22 %.
Selitän 28.11.2002 sarakkeessa, miten pelataan, kun jäljellä on vain kolme riviä. Tässä on strategiani neljälle riville. Kun on vuorosi, katso vasemman sarakkeen kokoonpano ja pelaa oikean sarakkeen ruudut. Esimerkiksi aloituskohta 3456 on listattu viimeisenä ja osoittaa, että sinun pitäisi poistaa 4 helmeä riviltä, jolla on 5 helmeä, jolloin jäljelle jää 1346. Jos vasemmassa sarakkeessa lukee "Häviä", ei ole mitään keinoa voittaa, jos vastustaja pelaa optimaalista strategiaa, kuten Transciencen peli näyttää aina tekevän.
Tämän taulukon kaava näyttää olevan sellainen, että vastustaja pakotetaan tilanteeseen, jossa pienimmän ja suurimman rivin helmien summa on yhtä suuri kuin kahden keskimmäisen rivin summa. Tämä tarkoittaisi, että riville, jolla on vähiten helmiä, jätetään nolla.
Helmet ennen sikaa II -strategia
| Sinulla on | Lähtö |
| 1111 | 111 |
| 1112 | 111 |
| 1113 | 111 |
| 1114 | 111 |
| 1115 | 111 |
| 1116 | 111 |
| 1122 | Menettää |
| 1123 | 1122 |
| 1124 | 1122 |
| 1125 | 1122 |
| 1126 | 1122 |
| 1133 | Menettää |
| 1134 | 1133 |
| 1135 | 1133 |
| 1136 | 1133 |
| 1144 | Menettää |
| 1145 | 1144 |
| 1146 | 1144 |
| 1155 | Menettää |
| 1156 | 1155 |
| 1222 | 1122 |
| 1223 | 1122 |
| 1224 | 1122 |
| 1225 | 1122 |
| 1226 | 1122 |
| 1233 | 123 |
| 1234 | 123 |
| 1235 | 123 |
| 1236 | 123 |
| 1244 | 1144 |
| 1245 | 145 |
| 1246 | 246 |
| 1255 | 1155 |
| 1256 | Menettää |
| 1333 | 1133 |
| 1334 | 1133 |
| 1335 | 1133 |
| 1336 | 1133 |
| 1344 | 1144 |
| 1345 | 145 |
| 1346 | Menettää |
| 1355 | 1155 |
| 1356 | 1256 |
| 1444 | 1144 |
| 1445 | 1144 |
| 1446 | 1144 |
| 1455 | 1155 |
| 1456 | 1346 |
| 2222 | Menettää |
| 2223 | 2222 |
| 2224 | 2222 |
| 2225 | 2222 |
| 2226 | 2222 |
| 2233 | Menettää |
| 2234 | 2233 |
| 2235 | 2233 |
| 2236 | 2233 |
| 2244 | Menettää |
| 2245 | 2244 |
| 2246 | 2244 |
| 2255 | Menettää |
| 2256 | 2255 |
| 2333 | 2233 |
| 2334 | 2233 |
| 2335 | 2233 |
| 2336 | 2233 |
| 2344 | 2244 |
| 2345 | Menettää |
| 2346 | 1346 |
| 2355 | 2255 |
| 2356 | 2345 |
| 2444 | 2244 |
| 2445 | 2244 |
| 2446 | 2244 |
| 2455 | 2255 |
| 2456 | 2345 |
| 3333 | Menettää |
| 3334 | 3333 |
| 3335 | 3333 |
| 3335 | 3333 |
| 3336 | 3333 |
| 3344 | Menettää |
| 3345 | 3344 |
| 3346 | 3344 |
| 3355 | Menettää |
| 3356 | 3355 |
| 3444 | 3344 |
| 3445 | 3344 |
| 3446 | 3344 |
| 3455 | 3355 |
| 3456 | 1346 |
Brad S. kirjoitti lisätäkseen yleisen strategian mille tahansa määrälle helmiä ja rivejä. Ensin jaat jokaisen rivin binäärikomponentteihinsa. Esimerkiksi Transcience-pelin lähtötilanne olisi seuraava.
- 3 = 2 + 1
- 4 = 4
- 5 = 4+1
- 6 = 4 + 2
Sitten pyrit jättämään parillisen määrän jokaista 2:n potenssia. Esimerkiksi yllä olevassa on kaksi ykköstä, kaksi kakkosta ja kolme nelosta. Joten jäljelle jää yksi ylimääräinen 4. Sitten poistat 4 miltä tahansa riviltä, jonka termi on 4. Jatka tätä, kunnes saat vastustajasi luvuksi 2, 2 tai parittoman määrän ykkösiä.
Kokeile tätä strategiaa Pearl 3 -pelissä, niin voitat joka kerta. Jos aloitat häviävällä skenaariolla, kuten minä tein pelissä 10 (4+7+8+11), voit napsauttaa "mene"-painiketta saadaksesi hänet aloittamaan.
En ymmärrä NIM- peliäsi! Olen aina ajatellut, että voittamisen avain on jättää vastustajalle (tässä tapauksessa tietokoneelle) pisteitä, joiden summa on seuraavaksi pienin luku, joka on yhtä suuri kuin niiden summa binäärilukuina. Eli jos minulla on 17 pistettä, otan niistä 2 ja jätän jäljelle 15, binäärilukujen 1, 2, 4 ja 8 summan. Mutta tämä ei näytä toimivan. Olenko oikeassa vai väärässä?
Olet oikeilla jäljillä binäärilukujen kanssa, mutta se ei ole aivan voittava strategia. Ensinnäkin, jos voit jättää vastustajallesi parittoman määrän rivejä, joissa on yksi kappale kutakin, tee niin. Muussa tapauksessa jaa jokainen rivi binäärikomponentteihinsa. Esimerkiksi 99 olisi 64 + 32 + 2 + 1. Laske sitten yhteen kunkin komponentin lukumäärä kaikilla riveillä. Etsi sitten pelitapa, jossa vastustajallesi jää parillinen määrä kaikkia binäärikomponentteja kaikilla riveillä.
Katsotaanpa esimerkkiä. Oletetaan, että on sinun vuorosi seuraavassa tilanteessa.
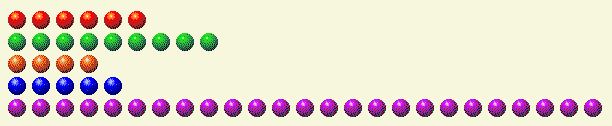
Seuraava taulukko jakaa jokaisen rivin binäärikomponentteihinsa.
Pelaajan vuoro 1
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Kokonais | 3 | 1 | 3 | 2 | 1 |
Kuten näet, lukuja ykköset, kakkoset, neloset ja kuusitoista on pariton määrä. Meidän on selvästi saatava luku 25 alle luvun 16, jotta yksikkö 16 poistuu. Jotta binäärikomponenttien summa pysyisi tasoissa, meidän on poistettava luku 1, lisättävä luku 2, lisättävä luku 4, säilytettävä luku 8 ja poistettava luku 16. Tämä tarkoittaa, että paras peli on 2+4+8=14 viimeisellä rivillä. Jättämällä luvun 14 alimmalle riville saadaan seuraava.
Tietokoneen vuoro 1
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Kokonais | 2 | 2 | 4 | 2 | 0 |
Tietokone tekee vuoronsa, ja meille jää tämä.
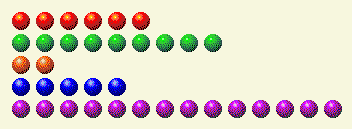
Tässä on sen binaarinen erittely.
Pelaajan vuoro 2
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Kokonais | 2 | 3 | 3 | 2 | 0 |
Tässä meidän on poistettava 2 ja 4, jotta summat saadaan tasaluvuksi. Rivejä on vain yksi, 14, jolla on molemmat komponentit. Poista siis siitä 6, jolloin jäljelle jää 8.
Tietokoneen vuoro 2
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Kokonais | 2 | 2 | 2 | 2 | 0 |
Tietokone tekee vuoronsa, ja meille jää tämä.
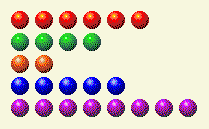
Nyt meidän on muutettava sarakkeet 1, 4 ja 8.
Pelaajan vuoro 3
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Kokonais | 1 | 2 | 3 | 1 | 0 |
Tämä voidaan tehdä muuttamalla rivi 8 riviksi 5 seuraavasti.
Tietokoneen vuoro 3
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| Kokonais | 2 | 2 | 4 | 0 | 0 |
Tietokone tekee vuoronsa, ja meille jää tämä.
Nyt meidän on muutettava kokonaismäärät 2 ja 4.
Pelaajan vuoro 4
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Kokonais | 2 | 3 | 3 | 0 | 0 |
Tämä onnistuu muuttamalla luvun 6 arvoksi 0.
Tietokoneen vuoro 4
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Kokonais | 2 | 2 | 2 | 0 | 0 |
Tietokone tekee vuoronsa, ja meille jää tämä.
Nyt meidän täytyy vaihtaa kakkoset ja neloset.
Pelaajan vuoro 5
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Kokonais | 2 | 3 | 1 | 0 | 0 |
Tämä voidaan saavuttaa muuttamalla rivin 5 riviksi 3. Jos saat vastustajasi x,x,y,y -tilanteeseen, et voi muuta kuin voittaa, jos pystyt ylläpitämään saman tilanteen loppuun asti.
Tietokoneen vuoro 5
| Rivi | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Kokonais | 2 | 4 | 0 | 0 | 0 |
Seuraavien siirtojen ajan pidän tietokoneen x,x,y,y-kuvioissa. Tässä tietokone jättää minulle 2,2,3,2; joten minä jätän sen 2,2,2,2:een.

Tietokone antaa minulle sitten 2,2,1,2. Jätän sen 2,2,1,1:een.
Tietokone jättää minulle sitten 2,2,1. Minä jätän sen 2,2:een. Jos saat vastustajasi kahdelle yhtä suurelle riville, et voi muuta kuin voittaa, pidä rivit vain yhtä suurina.

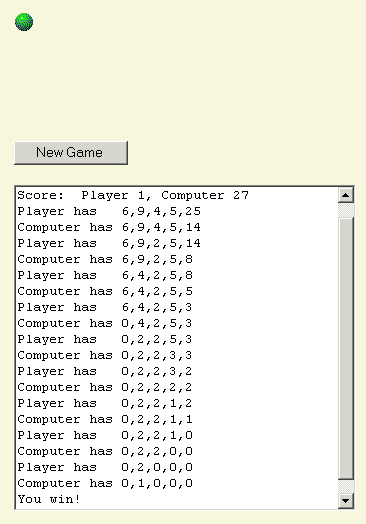
Tietokone jättää minulle sitten yhden kahden kirjan pinon, ja poistan niistä yhden.

Tässä on pelin loppu.
Hankin hiljattain isoisosedälleni kuuluneen karnevaalipyörän. Se on noin sata vuotta vanha ja yritän kehittää peliä sen ympärille. Se on numeroitu satunnaisessa järjestyksessä 1-60 ja siinä vuorottelevat musta ja punainen, ja vihreä tähti on joka viidennessätoista merkissä. Voisitko auttaa minua hahmottelemaan, kuinka paljon voittoja kullakin pyöräytyksellä pitäisi olla?
Joten mustia lukuja on 30, punaisia 30 ja vihreää 4. Tämä tekisi mustan todennäköisyydeksi 30/64, punaisen 30/64 ja vihreän 4/64. Jos tapahtuman todennäköisyys on p, niin reilut kertoimet ovat (1 - p) / p = 1. Joten minkä tahansa punaisen reilut kertoimet olisivat (34/64) / (30/64) = 34 - 30 = 17 - 15. Sama pätee mustaan. Vihreän reilut kertoimet ovat (60/64) / (4/64) = 60 - 4 = 15 - 1. Tietylle luvulle reilut kertoimet ovat (63/64) / (1/64) - 63 - 1.
Ehdotan, että punaiselle ja mustalle panostetaan 1:1, vihreälle 14:1 ja mille tahansa yksittäiselle numerolle 60:1. Yksi talon edun kaava on (ta)/(t+1), jossa t on todellinen kertoin ja a on varsinainen kertoin. Tässä tapauksessa talon etu punaisella tai mustalla panoksella on (63-60)/(63+1) = 3/64 = 4,69 %. Vihreällä panoksella talon etu on (15-14)/(15+1) = 1/16 = 6,25 %. Yksittäisillä numeroilla talon etu on (63-60)/(63+1) = 3/64 = 4,69 %.
New Yorkin osavaltiossa on videoarpajaispäätteitä (VLT) vedonlyöntipaikoilla, jotka eivät ole pelimerkkejä. Kuulet termin "kone lähestyy asetuspistettään", kun VP-kone "kuumenee" ja jakaa voittavan käden toisensa jälkeen. Tämä selittäisi, miksi sama kone maksaa yhtenä päivänä ja ei halua tietää sinua muina päivinä. Lisäksi useimmat näistä koneista eivät anna sinun hävitä jaettua voittavaa kättä. Heitä se pois, niin se palauttaa vastaavan käden tai paremman. Mitä mieltä olet tästä aiheesta?
VLT:t ovat hienostuneita pull-tab-pelejä. Niissä on ennalta määrätty joukko tuloksia. Kun pelaat, peli valitsee satunnaisesti tuloksen ja näyttää voiton pelaajalle kolikkopelin tai videopokerin muodossa. Koska tulos on ennalta määrätty, kaikki taitoelementit ovat kuvitteellisia. Esimerkiksi jos saat kuningasvärisuoran ja heität sen pois, saat toisen nostettaessa. Yleensä sanon, että uhkapelaamisessa menneisyydellä ei ole merkitystä, mutta tässä tapauksessa on olemassa poistamisen vaikutus. Jos pelaat kerran ja häviät, se parantaa hieman jäljellä olevien pelitulosten todennäköisyyksiä, kunnes virtuaalisten pull-tab-korttien tarjonta on loppunut ja oletan, että virtuaalinen rumpu täyttyy uudelleen. Uskon, että kuumat ja kylmät heilahtelusi ovat vain normaalia onnea, ja kaikki ennalta määrätyt kortit ovat kuvitteellisia.
Myöhemmin eräs lukija lisäsi tähän aiheeseen seuraavan.
Minulla on kommentti 14. helmikuuta julkaistuun "Kysy velholta" -kolumniisi (nro 183). Sillä ei oikeastaan ole mitään tekemistä vastaamasi kysymyksen kanssa. Se on vain asia, joka saattaa kiinnostaa sinua.
Ennen ehdotuksen 1A hyväksymistä, joka mahdollisti täyden luokan 3 pelaamisen, meillä oli pieni VLT-tyylinen asennus parin vuoden ajan. Järjestelmässämme, jota ylläpiti SDG (nykyään osa Ballyä), palkintopotti alkoi 4 miljoonalla arvonnalla. Kun potti pieneni ja jäljellä oli 2 miljoonaa, lisättiin seuraava 4 miljoonan potti, jolloin arvonnan kokonaismääräksi tuli 6 miljoonaa. Kun potti pieneni jälleen 2 miljoonaan, prosessi toistui.
Kuinka monta heittoa odotetaan tarvittavan Yahtzeen saamiseksi?
Olettaen, että pelaajalla on aina eniten edustettuna oleva numero, keskiarvo on 11,09. Tässä on taulukko, joka näyttää heittojen lukumäärän jakauman 82,6 miljoonan yrityksen satunnaissimulaatiossa.
Yahtzee-kokeilu
| Rullat | Esiintymiset | Todennäköisyys |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0,0333975 |
| 4 | 4504806 | 0,0545376 |
| 5 | 5776444 | 0,0699327 |
| 6 | 6491538 | 0,0785901 |
| 7 | 6727992 | 0,0814527 |
| 8 | 6601612 | 0,0799227 |
| 9 | 6246388 | 0,0756221 |
| 10 | 5741778 | 0,0695131 |
| 11 | 5174553 | 0,0626459 |
| 12 | 4591986 | 0,0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0,042285 |
| 15 | 3008766 | 0,0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0,0265529 |
| 18 | 1864107 | 0,0225679 |
| 19 | 1575763 | 0,019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0,0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0,00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0,00392347 |
| 29 | 271321 | 0,00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| Kokonais | 82600000 | 1 |
Tiedätkö mitään verkkosivustoa, jolla on hyvä analyysi backgammonin kertoimista/tilastoista/todennäköisyyksistä, ja onko olemassa tiettyjä kirjoja, joita voit suositella mistä tahansa pelin osa-alueesta?
Backgammon on yksi suosikkiuhkapeleistäni. En kirjoita siitä, koska pelaaja vastaan pelaaja -pelejä on erittäin vaikea analysoida. En myöskään tunnu löytävän pelistä mitään uutta. Joten jätän neuvot muille. Tässä ovat ehdotukseni resursseista:
Backgammon , kirjoittanut Paul Magriel: Jos olisi olemassa Raamattu backgammonille, se olisi tämä. Olen ylpeä vanhan kovakantisen laitoksen omistaja. Tämä kirja olisi loistava lähtökohta. Vaikka se on kirjoitettu vuonna 1976, neuvot pitävät edelleen hyvin paikkansa.
501 Essential Backgammon Problems, kirjoittanut Bill Robertie: Olen yrittänyt lukea tätä kirjaa vuosia, ja olen vieläkin vasta puolivälissä. On lannistavaa, jos puolet tehtävistä tulee väärin, niin että luulen olevani yhtä huono backgammonissa kuin golfissakin. Jokaisesta ratkaisematta jääneestä tehtävästä on kuitenkin opittavaa arvokkaalla tavalla. Keskitason ja edistyneille pelaajille tämä kirja on arvokas ja nöyräksi tekevä oppimistyökalu.
Snowie backgammon -ohjelmisto : Pelaan tätä peliä vastaan noin 1000 peliä vuodessa. Snowie ei ainoastaan pelaa lähes täydellistä peliä, vaan se kertoo tarkalleen, kuinka kalliiksi virheesi tulevat, kun teet niitä. On monia muita ominaisuuksia, joita en ole koskaan tutkinut. Jos olen oppinut Snowiesta yhden asian, niin sen, että pelini suurin ongelma on typerät virheet, joissa en aina näe täysin ilmeisiä pelikuvioita. Aivan kuten shakissa, yksi huono siirto voi pyyhkiä pois 100 hyvää siirtoa.
Motif-verkkosivusto : Ennen kuin ostin Snowien, pelasin lukemattomia pelejä Motifia vastaan. Motifin käyttämä strategia on mielestäni erittäin vankka. Mikään ei paranna omaa peliäsi niin kuin pelaaminen vahvempaa vastustajaa vastaan.
Seuraava taulukko näyttää kunkin pelaajan voittotodennäköisyyden ensimmäisen pelaajan ensimmäisen pyöräytyksen mukaan, jossa pelaaja 1 aloittaa, sitten pelaaja 2 ja pelaaja 3 viimeisenä. Alin rivi näyttää voittotodennäköisyydet kokonaisuudessaan ennen ensimmäistä pyöräytystä.
Todennäköisyydet Price is Right -näyttelyssä
| Pyöräytys 1 | Strategia | Pelaaja 1 | Pelaaja 2 | Pelaaja 3 |
| 0,05 | pyörähdys | 20,59 % | 37,55 % | 41,85 % |
| 0,10 | pyörähdys | 20,59 % | 37,55 % | 41,86 % |
| 0,15 | pyörähdys | 20,57 % | 37,55 % | 41,87 % |
| 0,20 | pyörähdys | 20,55 % | 37,55 % | 41,9 % |
| 0,25 | pyörähdys | 20,5 % | 37,56 % | 41,94 % |
| 0,30 | pyörähdys | 20,43 % | 37,56 % | 42,01 % |
| 0,35 | pyörähdys | 20,33 % | 37,58 % | 42,10 % |
| 0,40 | pyörähdys | 20,18 % | 37,60 % | 42,22 % |
| 0,45 | pyörähdys | 19,97 % | 37,64 % | 42,39 % |
| 0,50 | pyörähdys | 19,68 % | 37,71 % | 42,61 % |
| 0,55 | pyörähdys | 19,26 % | 37,81 % | 42,93 % |
| 0,60 | pyörähdys | 18,67 % | 37,96 % | 43,36 % |
| 0,65 | pyörähdys | 17,86 % | 38,21 % | 43,93 % |
| 0,70 | pysyä | 21,56 % | 38,28 % | 40,16 % |
| 0,75 | pysyä | 28,42 % | 35,21 % | 36,38 % |
| 0,80 | pysyä | 36,82 % | 31,26 % | 31,92 % |
| 0,85 | pysyä | 46,99 % | 26,35 % | 26,66 % |
| 0,90 | pysyä | 59,17 % | 20,36 % | 20,47 % |
| 0,95 | pysyä | 73,61 % | 13,19 % | 13,21 % |
| 1.00 | pysyä | 90,57 % | 4,72 % | 4,72 % |
| Keskimäärin | 30,82 % | 32,96 % | 36,22 % |
Tässä on voittoyhdistelmien määrä 6×20 6 mahdollisesta vaihtoehdosta.
Pelaaja 1: 118 331 250Pelaaja 2: 126 566 457
Pelaaja 3: 139 102 293
Mikä on oikea strategia Acey Deuceyn pelaamiseen kotipokeripelissä? Pelitapamme on, että jos kolmas kortti on yksi kahdesta ensimmäisestä, panos on tasapeli.
Pelitavassasi, jossa kolmannen kortin ottelu on tasapeli, kertoimet kääntyvät eduksi, kun kahden ensimmäisen kortin välillä on vähintään kuusi rankkia (kuuden kortin tasoitus). Omassa pelitavassani Orange Countyssa kolmannen kortin ottelu johti tuplahäviöön. Tämän säännön mukaan kertoimet ovat nollapisteessä kahdeksan kortin tasoituksella. Jos kolmannen kortin ottelu johtaa 1x tappioon, tarvitset seitsemän kortin tasoituksen, jotta kertoimet olisivat eduksi.
Yhden kortin pokerissa on kolmen kortin pakka: ässä, kakkonen ja kolmoset. Ässä on pienin ja kolmoset suurin. Kaksi pelaajaa panostaa kumpikin 1 dollarin pottiin. Sitten kumpikin pelaaja saa yhden kortin. Panostusjärjestys on ennalta määrätty, pelaaja 1 toimii ensin. Pelaaja 1 voi joko panostaa 1 dollarin tai sököttää. Jos pelaaja 1 panostaa, pelaaja 2 voi joko maksaa tai luovuttaa. Jos pelaaja 1 sököttää, pelaaja 2 voi joko panostaa 1 dollarin tai sököttää. Jos pelaaja 1 sököttää ja pelaaja 2 panostaa, pelaaja 1 voi joko maksaa tai luovuttaa. Jos molemmat pelaajat sököttävät tai molemmat panostavat, korkeampi kortti voittaa potin. Olettaen, että molemmat pelaajat ovat täydellisiä loogikoita, mikä on optimaalinen strategia kummallekin pelaajalle?
Toivottavasti olet tyytyväinen; käytin tähän koko päivän. Vastaus ja ratkaisu löytyvät toiselta sivustoltani mathproblems.info , tehtävästä 203 tai Jason Swansonin akateemisesta artikkelista Peliteoria ja pokeri .
Olen etsimässä asuntolainaa eri yhtiöiltä. Yksi yhtiö tarjoaa 5,75 % korkoa plus yhden prosenttiyksikön 30 vuoden kiinteälle lainalle. Toinen yhtiö veloittaa 5,875 % korkoa ilman prosenttiyksikköä. Kumpi tarjous on parempi?
Muiden lukijoiden tiedoksi, piste on lainasta veloitettava palkkio. Esimerkiksi 250 000 dollarin lainassa yksi piste olisi 2 500 dollaria. Oletan, että lainanottaja lisäisi pisteen pääomaan eikä koskaan maksaisi pääomaa pois ennenaikaisesti.
Seuraava taulukko näyttää vastaavan koron ilman pistettä yhden pisteen korolle ja laina-ajalle.
Vastaava korko ilman pisteitä
| Korko yhdellä pisteellä | 10 vuotta | 15 vuotta | 20 vuotta | 30 vuotta | 40 vuotta |
| 4,00 % | 4,212 % | 4,147 % | 4,115 % | 4,083 % | 4,067 % |
| 4,25 % | 4,463 % | 4,398 % | 4,366 % | 4,334 % | 4,318 % |
| 4,50 % | 4,714 % | 4,649 % | 4,617 % | 4,585 % | 4,570 % |
| 4,75 % | 4,965 % | 4,900 % | 4,868 % | 4,836 % | 4,821 % |
| 5,00 % | 5,216 % | 5,151 % | 5,119 % | 5,088 % | 5,073 % |
| 5,25 % | 5,467 % | 5,402 % | 5,370 % | 5,339 % | 5,324 % |
| 5,50 % | 5,718 % | 5,654 % | 5,621 % | 5,590 % | 5,576 % |
| 5,75 % | 5,969 % | 5,905 % | 5,873 % | 5,842 % | 5,827 % |
| 6,00 % | 6,220 % | 6,156 % | 6,124 % | 6,093 % | 6,079 % |
| 6,25 % | 6,471 % | 6,407 % | 6,375 % | 6,344 % | 6,330 % |
| 6,50 % | 6,723 % | 6,658 % | 6,626 % | 6,596 % | 6,582 % |
| 6,75 % | 6,974 % | 6,909 % | 6,878 % | 6,847 % | 6,834 % |
| 7,00 % | 7,225 % | 7,160 % | 7,129 % | 7,099 % | 7,085 % |
| 7,25 % | 7,476 % | 7,412 % | 7,380 % | 7,350 % | 7,337 % |
| 7,50 % | 7,727 % | 7,663 % | 7,631 % | 7,602 % | 7,589 % |
| 7,75 % | 7,978 % | 7,914 % | 7,883 % | 7,853 % | 7,841 % |
| 8,00 % | 8,229 % | 8,165 % | 8,134 % | 8,105 % | 8,093 % |
| 8,25 % | 8,480 % | 8,416 % | 8,385 % | 8,357 % | 8,344 % |
| 8,50 % | 8,731 % | 8,668 % | 8,637 % | 8,608 % | 8,596 % |
| 8,75 % | 8,982 % | 8,919 % | 8,888 % | 8,860 % | 8,848 % |
| 9,00 % | 9,233 % | 9,170 % | 9,140 % | 9,112 % | 9,100 % |
| 9,25 % | 9,485 % | 9,421 % | 9,391 % | 9,363 % | 9,352 % |
| 9,50 % | 9,736 % | 9,673 % | 9,642 % | 9,615 % | 9,604 % |
| 9,75 % | 9,987 % | 9,924 % | 9,894 % | 9,867 % | 9,856 % |
| 10,00 % | 10,238 % | 10,175 % | 10,145 % | 10,119 % | 10,108 % |
Tämä osoittaa, että 5,75 %:n korko yhdellä prosenttiyksiköllä vastaa 5,842 %:n korkoa ilman prosenttiyksiköt. Toisin sanoen maksu olisi sama molempiin suuntiin olettaen, että veloitettu prosenttiyksikkö lisätään pääomaan. Toinen tarjouksesi oli 5,875 % ilman prosenttiyksikköä, mikä on korkeampi kuin 5,842 %, joten ottaisin 5,75 %:n koron prosenttiyksikköineen.
PS. Niille teistä, jotka ihmettelette, miten ratkaisin i:n, käytin Excelin rate-funktiota .
Poikani teki juuri kaksi reikää yhdellä kertaa, kahden viikon aikana. Mitkä ovat kertoimet? Pojallani on tasoitus 1. Ensimmäinen reikä on 151 jaardia ja toinen 137 jaardia, kahdella eri kentällä.
Gregory Baerin Life: the Odds (and How to Improve Them) -kirjan mukaan PGA-kiertueen par 3 -reiällä hole-in-one-tuloksen todennäköisyys on 1:2491. Uskon, että nuo etäisyydet sijoittuvat par 3 -alueelle.
Tasoitus 1 on pirun hyvä, joten en aio antaa paljoa alennusta PGA Tourin pelaajiin verrattuna. Oletetaan, että poikasi todennäköisyys par 3 -reikää kohden on 1/3 000. Tyypillisellä Gold Course -kentällä on noin neljä par 3 -reikää. Oletetaan, että poikasi pelaa joka päivä. Se tekisi 28 par 3 -reikää viikossa. Todennäköisyys saada tasan kaksi reikää yhden reiän sisään olisi yhteensä (28,2)×(1/3000) ² ×(2999/3000) ²² = 1/24 017.
Osallistuin hiljattain arvontaan, jossa oli 7 033 palkintoa ja heidän mukaansa voiton todennäköisyys on 1/13. Ostin 5 lippua. Mitkä ovat todelliset todennäköisyyteni voittaa jotain? Lisäksi on 40 suurta palkintoa. Mitkä ovat todennäköisyyteni voittaa suuri palkinto?
Yksinkertaisuuden vuoksi jätetään huomiotta se tosiasia, että mitä enemmän lippuja ostat, sitä alhaisemmaksi kunkin lipun arvo muuttuu, koska kilpailet itseäsi vastaan. Kaikkien viiden lipun häviämisen todennäköisyys on kuitenkin (12/13) 5 = 67,02 %. Joten ainakin yhden palkinnon voittamisen todennäköisyys on 32,98 %. Rummussa on yhteensä 7033 × 13 = 91 429 lippua ennen kuin ostat yhtään. 91 429 - 40 = 91 389 eivät ole suuria palkintoja. Todennäköisyys sille, ettei viidellä lipulla voita suuria palkintoja, on (91 389/91 429) 5 = 99,78 %. Joten ainakin yhden suuren palkinnon voittamisen todennäköisyys on 0,22 % eli 1/458.
Herttapelissä jokaiselle pelaajalle jaetaan 13 korttia. Eniten kortteja 13 maasta kutsutaan "pitkäksi maaksi", jossa voi olla 4–13 korttia. Mikä on todennäköisyys kullekin näistä kokonaisluvuista?
Todennäköisyydet pitkälle maalle hertassa
| Kortit | Yhdistelmät | Todennäköisyys |
| 4 | 222766089260 | 0.35080524800183 |
| 5 | 281562853572 | 0.44339660045899 |
| 6 | 105080049360 | 0.16547685914958 |
| 7 | 22394644272 | 0.03526640326564 |
| 8 | 2963997036 | 0.00466761219692 |
| 9 | 235237860 | 0.00037044541245 |
| 10 | 10455016 | 0.00001646424055 |
| 11 | 231192 | 0.00000036407412 |
| 12 | 2028 | 0.00000000319363 |
| 13 | 4 | 0.00000000000630 |
| Kokonais | 635013559600 | 1 |
Luvun 72 sääntö sanoo, että jaat vuotuisen tuoton luvulla 72, jolloin saat vuosien lukumäärän, joka kuluu rahojesi kaksinkertaistamiseen. Esimerkiksi sijoituksen, joka tuottaa 10 % vuodessa, arvon kaksinkertaistamiseen kuluu 72/10 = 7,2 vuotta. Hieman turha kysymykseni on, miksi 72?
Ensinnäkin "72-säännön" periaate on arvio ajasta, joka tarvitaan rahojesi kaksinkertaistamiseen, ei tarkka vastaus. Seuraava taulukko näyttää "72-säännön" arvot ja tarkan vuosien lukumäärän eri vuotuisilla koroilla.
72 sääntö – Vuotta rahan kaksinkertaistamiseen
| Korko | 72. sääntö | Tarkka | Ero |
|---|---|---|---|
| 0,01 | 72,00 | 69.66 | 2.34 |
| 0,02 | 36,00 | 35,00 | 1.00 |
| 0,03 | 24.00 | 23.45 | 0,55 |
| 0,04 | 18.00 | 17.67 | 0,33 |
| 0,05 | 14.40 | 14.21 | 0,19 |
| 0,06 | 12.00 | 11,90 | 0,10 |
| 0,07 | 10.29 | 10.24 | 0,04 |
| 0,08 | 9.00 | 9.01 | -0,01 |
| 0,09 | 8.00 | 8.04 | -0,04 |
| 0,10 | 7.20 | 7.27 | -0,07 |
| 0,11 | 6.55 | 6.64 | -0,10 |
| 0,12 | 6.00 | 6.12 | -0,12 |
| 0,13 | 5.54 | 5.67 | -0,13 |
| 0,14 | 5.14 | 5.29 | -0,15 |
| 0,15 | 4.80 | 4.96 | -0,16 |
| 0,16 | 4.50 | 4.67 | -0,17 |
| 0,17 | 4.24 | 4.41 | -0,18 |
| 0,18 | 4.00 | 4.19 | -0,19 |
| 0,19 | 3.79 | 3.98 | -0,20 |
| 0,20 | 3.60 | 3.80 | -0,20 |
Miksi 72? Sen ei tarvitse olla täsmälleen 72. Se on luku, joka toimii hyvin realistisilla koroilla, joita todennäköisesti näet sijoituksessa. Se toimii lähes täsmälleen 7,8469 %:n korolla. Luvussa 72 ei ole mitään erityistä, kuten π:ssä tai e:ssä. Miksi mikä tahansa luku toimii? Jos korko on i, ratkaistaan, kuinka monta vuotta (y) sijoituksen kaksinkertaistamiseen kuluu.
2 = (1 + i) y
ln(2) = ln(1 + i) y
ln(2) = y × ln(1 + i)
y = ln(2)/ln(1 + i)
Tämä ei ehkä ole paras vastaukseni ikinä, mutta yritä seurata tätä logiikkaa: olkoon y=ln(x).
dy/dx=1/x.
1/x =~ x, kun x:n arvot ovat lähellä yhtä.
Joten dy/dx = ~ 1, kun x:n arvot ovat lähellä yhtä.
Joten ln(x):n kulmakerroin on lähellä arvoa 1, kun x:n arvot ovat lähellä arvoa 1.
Joten ln(1+x):n kulmakerroin on lähellä arvoa 1, kun x:n arvot ovat lähellä nollaa.
"Luvun 72 sääntö" sanoo, että .72/i =~ .6931/ln(1+i).
Olemme osoittaneet, että i ja ln(1+i) ovat samankaltaisia, kun i:n arvot ovat lähellä nollaa.
Joten 1/i ja 1/ln(1+i) ovat samankaltaisia, kun i:n arvot ovat lähellä nollaa.
Luvun 72 käyttäminen 69,31:n sijaan korjaa i:n ja ln(1+i):n välisiä eroja noin 8 %:n i-arvoilla.
Toivottavasti tästä saa edes jotain selvää. Laskelmani on aika ruosteessa; meni tuntikausia selittää tämä itselleni.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Hiljattain katumarkkinoilla oli peli, jossa oli numerokenttä, matalat kupit ja kuppi palloja, ja siinä oli yhteenlaskua. En kysynyt pelin nimeä, ja etsin internetistä noin tunnin, mutta en löytänyt siitä mitään. Ajattelin, että teillä saattaisi olla tietoa siitä, sen kertoimista tai ainakin nimestä.
Pelin alan termi on Razzle Dazzle. Muistan nähneeni sen lapsena Etelä-Kaliforniassa ja viime vuonna San Felipessä Meksikossa. Se yleensä nyljetään näyttämään jalkapallo-ottelulta. Mielestäni tämä peli on pahin karnevaalipelihuijauksista. New Yorkin osavaltion pitäisi hävetä sen sallimisesta. Joidenkin tutkimusten perusteella säännöt vaihtelevat paikasta toiseen, mutta huijauksen ydin on aina sama.
Se perustuu samaan illuusioon kuin crapsin kenttäpanos. Niille lukijoille, jotka eivät tunne kenttäpanosta, pelaaja voittaa, jos kahden nopan heiton summa on 2, 3, 4, 9, 10, 11 tai 12. Häviävät numerot ovat 5, 6, 7 ja 8. Voitot maksavat tasarahaa, paitsi että 2 maksaa 2:1 ja 12 3:1 (paitsi pihien Harrah'sin kasinoiden kohdalla, joissa 2:1 maksetaan vain 12:lle). Matemaattisesti haastava uhkapeluri saattaa virheellisesti päätellä, että se on hyvä veto, koska voittoja on 7 ja häviäviä vain 4. Syy siihen, miksi kertoimet suosivat taloa, on se, että häviävillä numeroilla on suurin mahdollisuus tulla heitetyksi.
Tässä ovat Razzle Dazzlen tarkat säännöt Donald A. Berryn ja Ronald R. Regalin artikkelista Probabilities of Winning a Certain Carnival Game , joka ilmestyi The American Statistician -lehden marraskuun 1978 numerossa.
- Pelin tavoitteena on edetä jalkapallokentän poikki 100 jaardia. Pelaaja saa jonkinlaisen mukavan palkinnon, kun hän tekee niin.
- Pelaaja alkaa maksaa tiettyä maksua per peli, kuten 1 dollari.
- Pelaaja pudottaa kahdeksan marmorikuulaa 11 x 13 -ruudukolle. Jokainen marmori putoaa yhteen 143 reiästä.
- Jokaisella reiällä on pisteiden määrä 1–6. Seuraava taulukko näyttää kunkin pisteiden määrän esiintymistiheyden.
Razzle Dazzle -pisteiden jakautuminen
Pisteet Määrä
aluksellaTodennäköisyys 1 11 0,076923 2 19 0,132867 3 39 0,272727 4 44 0.307692 5 19 0,132867 6 11 0,076923 Kokonais 143 1.000000 - Pisteiden kokonaismäärä lasketaan yhteen. Pelaaja tarkistaa pistemäärän muuntotaulukosta nähdäkseen, kuinka monta jaardia pelaaja etenee. Muuntotaulukko näkyy alla.
Razzle Dazzlen muuntokaavio
Pisteet Jaardit
Saavutettu8 100 9 100 10 50 11 30 12 50 13 50 14 20 15 15 16 10 17 5 18–38 0 39 5 40 5 41 15 42 20 43 50 44 50 45 30 46 50 47 100 48 100 - Jos pelaaja heittää yhteensä 29, kaikkien seuraavien heittojen maksu kaksinkertaistetaan ja pelaaja saa yhden ylimääräisen palkinnon, jos ja kun hän saavuttaa jalkapallokentän toisen pään.
Keskimääräinen pistemäärä kuulaa kohden on 3,52 ja keskihajonta on 1,31. Huomaa, kuinka 3 ja 4 pisteellä on suurin todennäköisyys. Tämä pitää keskihajonnan pienenä ja useiden kuulaiden summan lähellä odotusta. Yhden nopan heiton keskihajonta on vertailun vuoksi 1,71.
Huomaa seuraavaksi, kuinka jaardimuunnostaulukossa on 20 voittoa ja 21 tappiota. Hölmöläinen, joka lyö vetoa karnevaalipeleistä, saattaa virheellisesti päätellä etenemistodennäköisyytensä olevan 20/41 eli 48,8 %. En yllättyisi, jos karnevaalipelaajat väittäisivät virheellisesti, että nämä olivat etenemistodennäköisyydet. Kuitenkin, aivan kuten kenttävedossa, todennäköisimmät tulokset eivät voita mitään.
Seuraava taulukko näyttää kunkin vuoroa kohden saavutettujen pisteiden, saavutettujen jaardien ja odotettujen saavutettujen jaardien todennäköisyyden. Oikeassa alakulmassa oleva solu näyttää, että keskimääräinen vuoroa kohden saavutettu jaardi on 0,0196.
Odotetut saavutetut jaardit vuoroa kohden
| Pisteet | Todennäköisyys | Jaardit Saavutettu | Odotettu Jaardit Saavutettu |
| 8 | 0.00000000005 | 100 | 0.00000000464 |
| 9 | 0.00000000176 | 100 | 0.00000017647 |
| 10 | 0.00000002586 | 50 | 0.00000129285 |
| 11 | 0.00000022643 | 30 | 0.00000679305 |
| 12 | 0.00000143397 | 50 | 0.00007169849 |
| 13 | 0.00000713000 | 50 | 0.00035650022 |
| 14 | 0.00002926510 | 20 | 0.00058530196 |
| 15 | 0.00010234709 | 15 | 0.00153520642 |
| 16 | 0.00031168305 | 10 | 0.00311683054 |
| 17 | 0.00083981462 | 5 | 0.00419907311 |
| 18 | 0.00202563214 | 0 | 0.00000000000 |
| 19 | 0.00441368617 | 0 | 0.00000000000 |
| 20 | 0.00874847408 | 0 | 0.00000000000 |
| 21 | 0.01586193216 | 0 | 0.00000000000 |
| 22 | 0.02642117465 | 0 | 0.00000000000 |
| 23 | 0.04056887936 | 0 | 0.00000000000 |
| 24 | 0.05757346716 | 0 | 0.00000000000 |
| 25 | 0.07566411880 | 0 | 0.00000000000 |
| 26 | 0.09221675088 | 0 | 0.00000000000 |
| 27 | 0.10431970222 | 0 | 0.00000000000 |
| 28 | 0.10958441738 | 0 | 0.00000000000 |
| 29 | 0.10689316272 | 0 | 0.00000000000 |
| 30 | 0.09677806051 | 0 | 0.00000000000 |
| 31 | 0.08125426057 | 0 | 0.00000000000 |
| 32 | 0.06317871335 | 0 | 0.00000000000 |
| 33 | 0.04540984887 | 0 | 0.00000000000 |
| 34 | 0.03009743061 | 0 | 0.00000000000 |
| 35 | 0.01833921711 | 0 | 0.00000000000 |
| 36 | 0.01023355162 | 0 | 0.00000000000 |
| 37 | 0.00520465303 | 0 | 0.00000000000 |
| 38 | 0.00239815734 | 0 | 0.00000000000 |
| 39 | 0.00099365741 | 5 | 0.00496828705 |
| 40 | 0.00036673565 | 5 | 0.00183367827 |
| 41 | 0.00011909673 | 15 | 0.00178645089 |
| 42 | 0.00003349036 | 20 | 0.00066980729 |
| 43 | 0.00000797528 | 50 | 0.00039876403 |
| 44 | 0.00000155945 | 50 | 0.00007797235 |
| 45 | 0.00000023832 | 30 | 0.00000714969 |
| 46 | 0.00000002632 | 50 | 0.00000131607 |
| 47 | 0.00000000176 | 100 | 0.00000017647 |
| 48 | 0.00000000005 | 100 | 0.00000000464 |
| Yhteensä | 1.00000000000 | 0 | 0.01961648451 |
Tässä on joitakin 17,5 miljoonan pelin satunnaissimulaation tuloksia.
Razzle Dazzle -simulaation tulokset
| Kysymys | Vastaus |
| Etenemisen todennäköisyys vuoroa kohden | 0,0028 |
| Odotetut saavutetut jaardit vuoroa kohden | 0,0196 |
| Odotetut saavutetut jaardit etenemistä kohden | 6.9698 |
| Odotetut vuorot ottelua kohden | 5238.7950 |
| Keskimäärin tuplaa ottelua kohden | 559.9874 |
| Keskimääräiset voitot peliä kohden | 560.9874 |
Olisin halunnut ilmoittaa pelin keskimääräisen kokonaispanoksen, mutta tietokoneeni ei pysty käsittelemään niin suuria lukuja. Keskimääräisessä pelissä pelaaja tuplasi panoksensa 560 kertaa, kun peliä kohden on keskimäärin 5 239 kierrosta. Yhdessä simulaatiopelissä pelaaja tuplasi panoksensa 1 800 kertaa. Jopa 560 tuplauksen keskiarvolla panos per heitto olisi 3,77 × 10⁻⁷ dollaria olettaen, että lähtöpanos on 1 dollari. Se on monta kertaluokkia suurempi kuin tunnetun maailmankaikkeuden atomien lukumäärä ( lähde ).
Naiivinkaan pelaaja ei pelaa kauaa, jos hän etenee vain kerran 355 pelissä. Karnevaalipelaajat huijaavat aluksi pelaajan eduksi. He saattavat havaita pelaajan ilmaisheitot tai valehdella pisteiden laskemisessa antaen pelaajalle voittosummia lisätäkseen itseluottamustaan. En ole koskaan pelannut peliä, mutta kuvittelen, että kun pelaaja pääsee lähelle punaista vyöhykettä (20 jaardia tai vähemmän touchdownista), karnevaalipelaaja alkaa pelata reilusti. Pelaaja saattaa ihmetellä, miksi hän yhtäkkiä ei pääse mihinkään, mutta kun rahat on jo sijoitettu ja hän on niin lähellä maaliviivaa, hän epäröisi kävellä pois ja luopua jo maksamastaan jaardista.
Linkit
- Razzle Dazzle , ote kirjasta On the Midway.
- Razzle Dazzle Carny -lautapelin kolikkopelihuijaus .
- Todennäköisyydet voittaa tietty karnevaalipeli, kirjoittanut Donald A. Berry ja Ronald R. Regal
Äskettäin järjestetyssä karnevaalissa tarjottiin ristinolla-tyylistä peliä. Yhdellä punnalla per kerta heität kolme uskomattoman pomppivaa palloa kohti suurta puista laatikkoa, jonka pohjassa on yhdeksän taskua. Olettaen, että jokainen pallo laskeutuu eri ruutuun, mikä olisi voittotodennäköisyys?
Kahdella eri tavalla voi voittaa: kolmella rivillä, kolmella sarakkeella ja kahdella lävistäjällä. Yhdistelmä (9,3) = 84 tapaa valita kolme ruutua yhdeksästä. Voiton todennäköisyys on siis 8/84 = 9,52 %.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mitä vinkkejä antaisit Monopolin pelaamiseen?
Tässä on velhoni perusstrategia Monopoliin:
- Osta kaikki. Kokeneet pelaajat saattavat tehdä poikkeuksia, jos kiinteistö ei auta sinua saavuttamaan monopoliasemaa, estää jonkun muun pelaamisen tai sillä on vain vähän arvoa neuvotteluvalttina. Myös yleishyödyllisistä palveluista voidaan kieltäytyä, jos rahat ovat vähissä.
- Käy kauppaa niin hyvin kuin pystyt. Tässä taito astuu kuvaan. Yritä vaihtaa parhaaseen mahdolliseen settiin. Tässä on yleisluontoinen paremmuusjärjestys: oranssi, keltainen, vaaleansininen, tummansininen, vaaleanvioletti, punainen, vihreä, tummanvioletti. Tämä vaihtelee olosuhteiden mukaan. Rahastoltaan niukassa pelissä suosi settejä, jotka ovat halvempia kehittää, kuten vaaleansinisiä. Rahastoltaan runsaassa pelissä valitse settejä, joihin on enemmän potentiaalia käyttää rahaa, kuten keltaisia tai tummansinisiä.
- Kun olet hankkinut tietyn sarjan, joko luonnollisesti tai kaupan kautta, rakenna sitä nopeasti. Yritä saada kolme taloa jokaiselle tontille mahdollisimman nopeasti. Talokohtainen marginaalituotto laskee kolmen jälkeen. Kiinnitä suurin osa muista kiinteistöistäsi ja käytä käteisesi. Haluat jättää hieman omaa pääomaa pieniä kuluja varten. Rahojesi käyttämättä jättäminen on kuin sotilas taistelussa ei käyttäisi luotejaan.
- Vastusta kaikkia typeriä talon sääntöjä. Tämä pätee erityisesti Free Parking -pelin rahapottiin (en voi sietää sitä!). Jos olet taitavampi kuin vastustajasi, haluat minimoida pelin satunnaisuuden.
Jos apina leikkisi Rubikin kuutiolla, mikä olisi todennäköisyys sille, että se olisi ratkaistussa kuviossa millä tahansa hetkellä?
Kuution kuusi keskisivua ovat kiinteät. Kääntämällä sivuja voit vain järjestää kulmat ja reunat uudelleen. Jos purkaisit kuution osiin, kahdeksan kulmaa voitaisiin järjestää 8! = 40 320 tavalla riippumatta kunkin palan suunnasta. Samoin 12 reunaa voitaisiin järjestää 12! = 479 001 600 tavalla riippumatta suunnasta.
Kukin kulma voidaan suunnata kolmella tavalla, yhteensä 3 * 8 = 6 561 kulmasuuntaa. Samoin kutakin reunakappaletta voidaan suunnata kahdella tavalla, yhteensä 2 * 12 = 4 096 reunasuuntaa.
Jos siis voisimme purkaa kuution osiin ja järjestää reuna- ja kulmaryhmät uudelleen, mahdollisia permutaatioita olisi 8! × 12! × 3 8 × 2 12 = 519 024 039 293 878 000 000. Kaikkia näitä permutaatioita ei kuitenkaan voida saada lähtökohdasta kiertämällä pintoja.
Ensinnäkin on mahdotonta kiertää vain yhtä kulmaa ja jättää kaikki muu samanlaiseksi. Mikään käännösten yhdistelmä ei saavuta tätä. Pohjimmiltaan jokaisella toiminnolla on oltava reaktio. Jos haluat kiertää yhtä kulmaa, se häiritsisi jotenkin muita nappuloita. Samoin on mahdotonta kaataa vain yhtä reunanappulaa. Näistä syistä meidän on jaettava permutaatioiden lukumäärä luvulla 3 × 2 = 6.
Toiseksi, kahta reunapalaa ei voida vaihtaa keskenään häiritsemättä kuution muuta osaa. Tämä on tämän vastauksen vaikein osa selittää. Rubikin kuutiolla voi vain kiertää yhtä sivua kerrallaan. Jokainen liike pyörittää neljää reunapalaa ja neljää kulmapalaa, jolloin siirretään yhteensä kahdeksaa palaa. Kiertosarja voidaan esittää kahdeksalla jaollisen määrän palasia liikkeinä. Usein siirtosarja johtaa kahden toisensa kumoavan liikkeen syntymiseen. Millä tahansa kiertosarjalla siirrettyjä palasia on kuitenkin aina parillinen määrä. Kahden reunapalan vaihtaminen olisi yksi liike, pariton luku, jota ei voida saavuttaa millään parillisten lukujen joukolla. Matemaatikot kutsuisivat tätä pariteettiongelmaksi. Joten meidän on jaettava vielä kahdella, koska kahta reunapalaa ei voida vaihtaa keskenään häiritsemättä muita paloja.
Rubikin kuution permutaatioita on siis 3 × 2 × 2 = 12 mahdollista ryhmää. Jos Rubikin kuutio purettaisiin ja koottaisiin takaisin satunnaisesti, on 1/12 mahdollisuus, että se olisi ratkaistavissa. Joten Rubikin kuution permutaatioiden kokonaismäärä on 8! × 12! × 3 12 × 2 12 / 12 = 43 252 003 274 489 900 000. Jos sinulla olisi seitsemän miljardia apinaa, suunnilleen ihmismaailman väkiluku, jotka leikkisivät Rubikin kuutiolla satunnaisesti yhden kierroksen sekunnissa nopeudella, kuutio kulkee ratkaistun paikan läpi keskimäärin kerran 196 vuodessa.
Linkit
Pelasin Heartsia ja minulle jaettiin niitä 10. Mitkä ovat todennäköisyydet?
Niille, jotka eivät tunne Herttapelin sääntöjä, peli aloitetaan jakamalla 13 korttia neljälle pelaajalle kullekin. Herttapelin maa on pelissä merkittävä, joten sillä, kuinka monta saat, on merkitystä. Seuraava taulukko näyttää todennäköisyydet saada 0–13 herttaa.
Todennäköisyys saada 0–13 sydäntä 13 kortista
| Sydämet | Yhdistelmät | Todennäköisyys | Käänteinen |
|---|---|---|---|
| 13 | 1 | 0.0000000000016 | 1/635 013 559 600,0 |
| 12 | 507 | 0.0000000007984 | 1/1 252 492 228,0 |
| 11 | 57 798 | 0.0000000910185 | 1/10 986 773,9 |
| 10 | 2 613 754 | 0.0000041160601 | 1/242 950,8 |
| 9 | 58 809 465 | 0.0000926113531 | 1/10 797,8 |
| 8 | 740 999 259 | 0.0011669030492 | 1/857,0 |
| 7 | 5 598 661 068 | 0.0088166008164 | 1/113,4 |
| 6 | 26 393 687 892 | 0.0415639752774 | 1/24,1 |
| 5 | 79 181 063 676 | 0.1246919258321 | 1/8,0 |
| 4 | 151 519 319 380 | 0.2386080062219 | 1/4,2 |
| 3 | 181 823 183 256 | 0.2863296074662 | 1/3,5 |
| 2 | 130 732 371 432 | 0.2058733541286 | 1/4,9 |
| 1 | 50 840 366 668 | 0.0800618599389 | 1/12,5 |
| 0 | 8 122 425 444 | 0.0127909480376 | 1/78,2 |
| Kokonais | 635 013 559 600 | 1.0000000000000 |
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Kasinokampanjoissa, joissa käytetään edelleen tavallisia lippuja oikeassa rummussa (eikä sähköisissä), joissa lippusi tulostetaan pelaajan tiskillä ja laitetaan rumpuun – taivutetaanko/rypistetäänkö lippuja ennen niiden laittamista rumpuun? Luuletko, että taivutetuilla lipuilla on paremmat mahdollisuudet tulla valituiksi?
Toivottavasti olet tyytyväinen. Vastatakseni tähän kysymykseen ostin Office Depotista ison rullan lippuja. Sitten laitoin 500 lippua paperipussiin, taittelin ne puoliksi noin 90 asteen kulmassa ja avasin toisen puolen. Sitten pyysin kuutta vapaaehtoista nostamaan kukin 40–60 lippua yksi kerrallaan ja lisäämään uuden laatikon, samalla kun kirjasin tulokset muistiin. Tässä ovat tulokset.
Lippujen arvontakokeilu
| Aihe | Taitettu | Avattu | Kokonais |
|---|---|---|---|
| 1 | 25 | 25 | 50 |
| 2 | 38 | 22 | 60 |
| 3 | 25 | 15 | 40 |
| 4 | 34 | 16 | 50 |
| 5 | 27 | 23 | 50 |
| 6 | 26 | 24 | 50 |
| Kokonais | 175 | 125 | 300 |
Joten 58,3 % arvotuista lipuista taitettiin!
Jos oletetaan, että luovuttamisella ei ollut vaikutusta, tulokset olisivat 2,89 keskihajonnan päässä odotuksista. Todennäköisyys saada näin monta tai enemmän luovutettua lippua, olettaen, että luovuttaminen ei vaikuttanut kertoimiin, on 0,19 % eli 1/514.
Voisin lisätä, että kiireesti arpoja nostaneet koehenkilöt nostivat paljon todennäköisemmin taitettuja arpoja. Ne, jotka ottivat jokaisen arvon huolellisesti ja ajoissa, olivat lähellä tai 50/50-jakaumaa.
Joten johtopäätökseni on ehdottomasti luovuttaa.
Keskustellaksesi tästä kysymyksestä, käy foorumillani Wizard of Vegasissa .