Todennäköisyys - Kolikot
Jos kolikkoa heitettäisiin 1000 kertaa, mikä on todennäköisyys, että kolikon päämäärä olisi 452–548?
Tähän ongelmaan voimme käyttää binomijakauman normaaliapproksimaatiota. Pään lukumäärän varianssi on 1000*(1/2)*(1/2)=250. Joten keskihajonta on 250 1/2 =15,8114. Todennäköisyys sille, että päätä on alle 548, on normdist((548+0,5-500)/15,8114) = 0,998920, jossa normdist on Excel-funktio, joka kuvaa todennäköisyyttä, että satunnaismuuttuja, jonka normaalijakauma on keskiarvo 0 ja keskihajonta 1, osuu annetun Z-luvun alle. Seuraavaksi vähennetään todennäköisyys sille, että päätä on alle 452. Tämä on normdist((452-0,5-500)/15,8114) = 0,001080. Joten vastaus on 0,99892-0,00108 = 0,997840. Jälleen kerran, tämä on approksimaatio. Varsinainen vastaus on 0,997856, mutta sen johtaminen on työläämpää. Kuinka usein pelaaja keskimäärin onnistuu saavuttamaan pisteen crapsissa saavutettuaan sen?
Olettaen, että piste syntyy 5/12 tapauksista, se on 6 tai 8, 4/12 tapauksista 5 tai 9 ja 3/12 tapauksista 4 tai 10. Todennäköisyys saada 6 tai 8 on 5/11, 5 tai 9 on 4/10 ja 4 tai 10 on 3/9. Joten pisteen syntymisen todennäköisyys, olettaen, että piste syntyi, on (5/12) * (5/11) + (4/12) * (4/10) + (3/12) * (3/9) = 40,61 %.
Herra velho, jos 50 eri ihmistä heittää kolikkoa ilmaan kahdeksan eri kertaa, kuinka monta prosenttia näistä 50 ihmisestä heittää kahdeksan peräkkäistä kruunaa tai klaavaa? Kiitos jo etukäteen.
Todennäköisyys sille, että joku heittää 8 kruunaa tai klaavaa, on 2 * (1/2) 8 = 1/128. Jos 50 ihmistä tekisi näin, keskimäärin 0,39 heistä saisi pelkät kruunat tai klaavat. Todennäköisyys sille, että ainakin yksi henkilö saisi pelkät kruunat tai klaavat, on 32,44 %.
Minulla on pussillinen 100 kolikkoa, joista yksi on kaksipäinen kolikko. Valitsen satunnaisesti kolikon ja sitten näen kolikon kääntyvän 10 kertaa peräkkäin. Mikä on todennäköisyys, että valitsin kaksipäisen kolikon?
Tämä on oppikirjan mukainen Bayes-ehdollinen todennäköisyyslaskelmatehtävä. Yleisesti ottaen A:n todennäköisyys tietyllä B:llä on A:n ja B:n todennäköisyys jaettuna B:n todennäköisyydellä. Tässä tapauksessa A heittää 10 kruunaa peräkkäin ja B valitsee kaksipäisen kolikon. A:n ja B:n todennäköisyys on 1/100. Tämä johtuu siitä, että kaksipäisen kolikon valitsemisen todennäköisyys on 1/100, ja jos näin tapahtuu, todennäköisyys saada 10 kruunaa peräkkäin on 100 %. Todennäköisyys saada 10 kruunaa peräkkäin, olettaen että kolikko valitaan satunnaisesti, on (1/100)*1 + (99/100)*(1/2) 10 . Tämä johtuu siitä, että kaksipäisen kolikon valitsemisen todennäköisyys on 1 %, jolloin saat 100 %:n todennäköisyyden, ja reilu kolikon valitsemisen todennäköisyys on 99 %, jolloin saat 10 kruunaa peräkkäin (1/2) 10 . Joten todennäköisyys sille, että valitsit kaksipäisen kolikon, olettaen, että käänsit 10 kruunaa peräkkäin, on 0,01/(0,01 * 1 + 0,99 * 0,000977) = 0,911843.
Onko sinulla vinkkejä kolikonheitolla lyömiseen vetoa?
Kyllä! Neuvoisin lyömään vetoa heiton alussa kuvapuoli ylöspäin. Science News Onlinen mukaan todennäköisyys sille, että kolikko putoaa samalle puolelle kuin se aloitti, on 51 %. Artikkelin mukaan syynä on se, että heitetty kolikko ei pyöri täydellisesti akselinsa ympäri ja joskus näyttää pyörivän, vaikka se ei todellisuudessa pyöri. Hypoteesi pätee vain, jos kolikko jää kämmenelle, joten pomppiminen ei ole ongelma. Artikkelissa sanotaan myös, että pyörivä penni pysähtyy klaavaan 80 % ajasta, koska painavampi klaavapuoli pyrkii putoamaan ensin. Olen kuitenkin tästä skeptinen. Yritin tätä 20 kertaa ja sain 11 kruunaa ja 9 klaavaa. Todennäköisyys saada 9 tai vähemmän klaavaa 20 pyöräytyksellä 80 %:n onnistumistodennäköisyydellä on 1:1775.
Uskon, että minulla saattaa olla vastaus pyörivään pennin ongelmaan. Yli kymmenen vuotta sitten tein kuudennella luokalla tiedeprojektin pennin pyörittämisestä. Luin Omni-lehdestä, että pennin pyörittäminen hyvin nopeasti pysäyttää melkein aina hännät ylöspäin, koska sivut kallistuvat kohti päitä. Kokeilin sitä satoja kertoja ja sain lähes puolueettomia tuloksia, paitsi kahdesti, kun se seisoi reunallaan.
Lukuisten tuntien hukkaamisen jälkeen huomasin vihdoin pyörittäväni sitä liian nopeasti, ja hitaampi pyöritys antoi minulle halutun tuloksen, eli hännät ylöspäin. Penni ei myöskään ole täysin tasainen, ja pyörityksen aloittaminen ohuimmasta kohdasta näytti lisäävän tasaisuutta. Muutama tyhjällä oleva taulukko ja jättimäinen pahvista tehty ympyrä, joka oli koristeltu pennin näköiseksi, toivat minulle kympin luonnontieteistä ja hylättyjä arvosanoja jokaisesta muusta aineesta, koska jätin kaikki kotitehtäväni huomiotta.
Olen siis todistanut kiistatta yhdellä karkealla, yli kymmenen vuotta sitten tehdyllä kokeella, josta en juurikaan muista mitään enkä oikein ymmärtänyt, mitä tein tuolloin, että ehkä pyörität penniäsi hieman liian nopeasti.
Okei, kokeilin tätä uudelleen pyörittämällä pennin hitaasti 100 kertaa. Hitaalla tarkoitan aikaa heilautuksen ja tuloksen ilmeisyyden välillä oli vähintään kaksi sekuntia, mutta alle viisi. Käytin kaunista kiiltävää 2004-D-penniä. Tulokseni oli 52 kruunaa ja 48 klaavaa. Joten en vieläkään ole vakuuttunut siitä, että pyörivä penni millään nopeudella suosii voimakkaasti klaavia.
Ymmärtääkseni tapahtuman "odotusaika" on kyseisen tapahtuman todennäköisyyden käänteisluku. Olen kiinnostunut laskemaan odotusajan peräkkäisten kakkosten heittämiseen yhdellä nopalla. Simulaatiossa saan keskimäärin 42 heittoa. Miten teen yhteyden peräkkäisten kakkosten heittämisen todennäköisyyteen?
On totta, että yksittäisten tapahtumien kohdalla, jos todennäköisyys on p, niin keskimääräinen odotusaika on 1/p. Peräkkäisten tapahtumien kohdalla tilanne kuitenkin monimutkaistuu. Olkoon x tila, jossa viimeinen heitto ei ollut kaksi. Tämä on myös tila alussa. Olkoon y tila, jossa viimeinen heitto oli kaksi. Ensimmäisen heiton jälkeen on 5/6 mahdollisuus, että olemme edelleen tilassa x, ja 1/6 mahdollisuus, että olemme tilassa y. Olkoon Ex(x) odotettu heittojen lukumäärä tilasta x ja Ex(y) odotettu heittojen lukumäärä tilasta y. Sitten...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), ja
Ex(y) = 1 + (5/6) * ex(x)
Ratkaisemalla nämä kaksi yhtälöä...
Esim.(x) = 1 + (5/6)*esimerkki(x) + (1/6)*(1 + (5/6)*esimerkki(x))
Ex(x) = 7/6 + (35/36) * Ex(x)
(1/36) * Ex(x) = 7/6
Esim.(x) = 36 * (7/6) = 42
Joten kahden peräkkäisen kakkosheiton keskimääräinen odotusaika on 42 rullaa.
Minulla on samanlainen ongelma, vain odotetut voltit kahden pään saamiseksi, matemaattisten tehtävien sivustollani, katso tehtävä 128.
Oletetaan, että meillä on uhkapeli. Heitetään toistuvasti puolueetonta kolikkoa. Jokaisella heitolla on maksettava 1 rupia. Mahdollisia tuloksia on kaksi: H tai T. Jos heitettyjen kolikoiden ja häntäkolikoiden välinen erotus on 3, saamme pelaajalta 8 rupiaa. Pitäisikö meidän pelata peliä ja miksi? Kuinka suuri on voittotodennäköisyytemme? Miten voittotodennäköisyyteen pitäisi vaikuttaa, jos saamme 7 tai 9 rupiaa?
Kutsutaan x:ää odotetuksi volttien lukumääräksi lähtöpisteestä.
Kutsutaan y:tä jäljellä olevien volttien odotetuksi lukumääräksi, jos toinen puoli on enemmistönä yksi voltti.
Kutsutaan z:tä jäljellä olevien volttien odotetuksi lukumääräksi, jos toisella puolella on enemmistönä kaksi volttia.
E(x) = 1 + E(y)
E(y) = 1 + 0,5*E(x) + 0,5*E(z)
E(z) = 1 + 0,5 * E(y)
Matriisialgebralla on helppo nähdä, että E(x) = 9, E(y) = 8 ja E(z) = 5. Keskimäärin tarvitaan 9 heittoa, jotta kruunan ja klaavan välinen ero on 3. Joten 8 rupian panoksella se on hyvä veto sille, joka saa yhden rupian heittoa kohden, koska hän saa keskimäärin 9 rupiaa, mutta maksaa takaisin vain 8. Talon etu pelaajalle on 11,11 %. 9 rupian panoksella se on reilu veto, 7 rupian panoksella talon etu on 22,22 %.
Kirjoituksessasi Kysy velholta 13. maaliskuuta 2006 annoit kolme kaavaa "rupia"-peliin. Vaikka ratkaisu on matemaattisesti oikea, en millään ymmärrä, miten nämä kolme yhtälöä mallintavat ongelmaa. Voitko kertoa, miten keksit nämä kolme yhtälöä?
Useat ihmiset pyysivät minua tarkentamaan vastaustani. Ratkaisu vaatii matriisialgebran perusteita.
Aloita määrittelemällä x vastaukseksi eli keskimääräiseksi volttien lukumääräksi, kunnes kruunan ja klaavan välinen ero on 3.
Olkoon y odotettu volttien lukumäärä pisteestä, jossa toinen puoli on yhden voltin verran ylöspäin.
Olkoon z odotettu volttien lukumäärä pisteestä, jossa toinen sivu on kahden voltin verran ylöspäin.
Ensimmäisen voltin jälkeen toinen puoli on enemmistössä yhden voltin verran. Joten x=1+y.
Kun jompikumpi puoli on yhden voltin edellä, toinen voltti johtaa joko alkutilanteeseen tasatilanteessa tai toiseen puoleen kahden voltin johdossa. Molemmat tulokset ovat yhtä todennäköisiä. Joten y=1+0.5*x + 0.5*z
Kun jompikumpi puoli on kahden voltin johdossa, toinen voltti johtaa joko jommankumman puoliskon yhden voltin johtoon tai peli päättyy. Jälleen molemmat tulokset ovat yhtä todennäköisiä. Joten z=1+0,5*y
Eli meillä on kolme yhtälöä ja kolme tuntematonta:
(1) X = 1 + y
(2) Y = 1 + 0,5x + 0,5z
(3) Z = 1 + 0,5 y
Ratkaistaan poistamalla ensin desimaaliluvut kertomalla kaksi viimeistä yhtälöä kahdella.
(1) X = 1 + y
(2) 2Y = 2 + x + z
(3) 2Z = 2 + y
Korvataan (2):n x arvolla 1+y yhtälöstä (1).
2Y = 2 + 1 + y + z
(4) y = 3 + z
Ei korvaavaa y:tä luvulla 3+z yhtälössä (3)
2z = 2 + 3 + z
z = 5
Korvaa nyt z luvulla 5 yhtälössä (4) saadaksesi
(5) y = 3 + 5 = 8
Ei korvaavaa y = 8 yhtälössä (1) saadaksesi
(6) × = 9
Ystäväni valitsee kolmen heiton sarjan, jossa on kruuna tai klaava, ja antaa minulle mahdollisuuden valita oman (erilaisen) kolmen heiton sarjan. Heitämme reilua kolikkoa niin monta kertaa kuin on tarpeen, kunnes yksi sarjoistamme tulee näkyviin. Jos hän valitsee HHH:n, minkä sarjan minun pitäisi valita, ja mikä on etuni tässä vedossa? Miten lasken, minkä sarjan valitsen hänen valitsemansa sarjan perusteella?
Seuraava taulukko näyttää pelaaja A:n voittotodennäköisyyden kaikkien mahdollisten pelaaja A:n ja pelaaja B:n valittujen kuvioiden mukaan.
Pelaajan A voittotodennäköisyys
| Pelaaja A | Pelaaja B | |||||||
| HHH | HHT | HTH | HTT | THH | THT | TTH | TTT | |
| HHH | 1/2 | 2/5 | 2/5 | 1/8 | 5/12 | 3/10 | 1/2 | |
| HHT | 1/2 | 2/3 | 2/3 | 1/4 | 5/8 | 1/2 | 7/10 | |
| HTH | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/8 | 7/12 | |
| HTT | 3/5 | 1/3 | 1/2 | 1/2 | 1/2 | 3/4 | 7/8 | |
| THH | 7/8 | 3/4 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| THT | 7/12 | 3/8 | 1/2 | 1/2 | 1/2 | 1/3 | 3/5 | |
| TTH | 7/10 | 1/2 | 5/8 | 1/4 | 2/3 | 2/3 | 1/2 | |
| TTT | 1/2 | 3/10 | 5/12 | 1/8 | 2/5 | 2/5 | 1/2 | |
Muistiväline optimaalisen kuvion valitsemiseksi on se, että hänen ensimmäisen ja toisen valintansa tulisi olla sinun toinen ja kolmas. Ensimmäisen valintasi tulisi olla kolmannen vastakohta. Esimerkiksi jos vastustajasi valitsee päänheiton, toisen ja kolmannen valintasi tulisi olla päänheitto. Viimeinen valintasi on T, joten ensimmäisen valintasi tulisi olla H päänheittokuviota varten. Tätä strategiaa noudattamalla voittotodennäköisyytesi on 2/3 - 7/8 riippuen vastustajasi valitsemasta kuviosta.
Hei, nimeni on Patty. Sinulla on todella hieno sivusto ja vaikutat erittäin asiantuntevalta mieheltä. Ehdottomasti juuri sellainen mies, jonka haluan rinnalleni kasinolla!!!!!!! Mietin, voisitko auttaa minua. Sanoin poikaystävälleni, että etsisin vastausta ongelmaan internetistä. Jos auttaisit minua, se saisi minut todella näyttämään hyvältä.
Poikaystäväni on kolikoiden keräilijä. Hän osti pussillisen vehnäpennejä. En itse tiedä paljoakaan kolikoista. (Hän opettaa minulle ajan myötä.) Mutta hän sanoi olevansa hämmästynyt siitä, ettei pussissa ollut yhtä tiettyä vuotta, koska ne ovat niin yleisiä. Hän sanoi, että todennäköisyys sille on miljardi yhteen. Sanoin hänelle, että yrittäisin kysyä toimistoni ihmisiltä (itseään neroiksi julistautuneilta!!), ja jos he eivät tiedä, yrittäisin tehdä vähän tutkimusta netissä. Löysin sinut.
Joka tapauksessa, jos voitte auttaa, arvostaisin sitä suuresti. Pussissa oli noin 5 500 penniä. Kaikkien Yhdysvaltojen rahapajojen lyömien vehnäpennien kokonaismäärä oli 24 267 000 000. Vuoden 1955 kolikoita (joita hän etsi) lyötiin 330 000 000. Jotkut toimistoni kaverit sanovat, että on muitakin tekijöitä, kuten väestötiedot, se, että rahapajat eivät ehkä ole jakaneet kaikkia pennejä jne. ...................... Olettaisin, että he ovat oikeassa, mutta minä (ja varmasti myös poikaystäväni) tyytyisimme tietämään likimääräiset kertoimet!!!!!!!!! Toivottavasti voitte auttaa.
Lyöntimääränne ovat lähellä Mountain View Coinsin lukuja. Olettaen, että jokaisella koskaan lyödyllä vehnäpennillä on sama todennäköisyys olla pussissa, todennäköisyys sille, että yksi pennin kolikko ei ole 55-koon kolikko, on (24 267 000 000 - 330 000 000) / 24 267 000 000 = 0,986401286. Todennäköisyys sille, että 5500 kolikkoa ei ole 55-koon kolikkoa, voidaan hyvin tarkasti arvioida olevan 0,986401286. 5500 = 1/507 033 772 284 213 000 000 000 000 000 000.
Isäni on kolikoiden keräilijä, joten pyysin häneltä apua tässä asiassa. Tässä mitä hän sanoi:
Tässä on arvaukseni. Vuonna 1955 Philadelphiassa lyötiin pieni määrä Lincolnin senttejä, joissa oli kaksi päivämäärää. Kukaan ei tiedä tarkalleen, kuinka monta. Ne sekoitettiin muiden senttien kanssa kiertoon ennen kuin virhe löydettiin. Kierrosta käyttämättä jäänyt kappale on nykyään arvoltaan noin 2000–6000 dollaria. Epäilen, että joku oli jo poiminut "vehnä"pussin kaikki vuoden 1955 kolikot etsiessään kaksinkertaisella stanssauksella varustettuja kolikoita. Tässä on kuva yhdestä: 1955 Doubled Die Averse One Cent .
Huomaa, että tällä verkkosivustolla myydään "vehnää", ja voit olla varma, että jonkin verran päivämääräkolikoiden karsimista on jo tapahtunut sen jälkeen, kun myyjä keräsi kolikot. Olisin luullut, että vuoden 1955 kolikot, joissa ei ollut kahta kuoletusleimaa, olisi palautettu kokoelmaan, mutta ehkä ne myydään erikseen tai sulatetaan. Vehnäpennien kupari on arvoltaan paljon enemmän kuin yksi sentti nykyään. Siksi he siirtyivät kuparipäällysteisiin sinkkisentteihin muutama vuosikymmen sitten. On mahdollista, että rahapaja itse päätti olla jakamatta monia vuoden 1955 kolikoita ja sulatti ne lyönnin jälkeen välttääkseen kiihkeän kamppailun harvinaisten kaksoiskuoletusleimattujen kolikoiden perässä. Rahapaja ja posti ovat aina olleet hämillään painovirheistä ja yrittävät pitää ne poissa kierrosta.
Oletan "likimääräisen", koska kolikkoa poistetaan, kun käydään läpi 5500 kolikkoa. Poiston vaikutus on todella mitätön! Tämä on hyvä esimerkki siitä, kuinka kohdekolikoiden todennäköisyys pienenee, kun poistetaan muita kuin kohteita, koska poistamisen vaikutus on niin pieni verrattuna paljon suurempaan todennäköisyyteen, että peli on kieroutunut eli kohdekolikot on poistettu.
Kyllä, sanoin "lähes likimääräinen", koska maailmassa on vain rajallinen määrä pennejä. Jos poistat pussista yhden muun kuin 55-dollarisen kolikon, poistamisen vaikutus lisää todennäköisyyttä, että joka toinen pussissa oleva penni on 55-dollarinen. Jos en olisi sanonut "lähes likimääräinen", ainakin kolme ihmistä olisi kirjoittanut korjatakseen minua. Se on tietenkin äärimmäisen pieni vaikutus, mutta monet lukijoistani ovat perfektionisteja ja hyppäävät kimppuuni pienimmistäkin virheistä.
Huoneessa on kaksi pöytää. Oikealla puolella on 100 kolikon pöytä, joista 20 on H-puoli ylöspäin ja loput (80) T-puoli ylöspäin. Toisella pöydällä ei ole kolikoita. Tavoitteena on jotenkin siirtää kolikot niin, että molemmilla pöydillä on yhtä monta H-puoli ylöspäin olevaa kolikoita. Kolikoita ei voi nähdä (pimeä huone) eikä niitä voi koskettaa, ovatko ne "ylöspäin" vai "alaspäin".
Mene ratkaisun löytämiseksi toiselle sivustolleni, mathproblems.info (spoilerivaroitus!)
Ystäväni tarjoutui lyömään vetoa 20,00 dollarista ja antamaan minulle 3:1 kertoimen, että jos heittäisin kolikkoa 100 kertaa, tulokseksi olisi tullut tasan 50 kruunaa ja 50 klaavaa. Jos niin olisi käynyt, olisin voittanut 60,00 dollaria, ja jos en olisi voittanut, olisin hänelle velkaa 20,00 dollaria. Olisiko minun pitänyt lyödä vetoa? Jos 50/50 ei ole todennäköisin tulos, onko olemassa toista tulosta (kuten 51/49), joka on todennäköisempi?
Todennäköisyys saada tasan 50 kumpaakin on yhdistelmä (100,50)*(1/2) 100 = 7,96%. Reilu kertoin olisi 11,56:1. Kertoimella 3:1 se on siis kamala veto, talon edun ollessa 68,2%. Kyseessä on joku kaveri, jolla on sellainen. 50/50 on todennäköisin tarkka jako kruunan ja klaavan välillä. Mielenkiintoinen veto on se, jääkö kruunan ja klaavan lukumäärä 47:n ja 53:n välille vai ei. Todennäköisyys jäädä tälle välille on 51,59%. Jos löydät jonkun lyömään vetoa, että kokonaismäärä jää tämän vaihteluvälin ulkopuolelle, sinulla olisi tasarahalla 3,18 %:n etu.
Seuraava taulukko näyttää todennäköisyyden kullekin 30–70 kruunalle/klaavalle.
Kruunan ja häntän kokonaismäärän todennäköisyys 100 heitolla
| Kruuna/Käsi | Todennäköisyys |
|---|---|
| 30, 70 | 0,000023 |
| 31, 69 | 0,000052 |
| 32, 68 | 0.000113 |
| 33, 67 | 0,000232 |
| 34, 66 | 0.000458 |
| 35, 65 | 0.000864 |
| 36, 64 | 0,001560 |
| 37, 63 | 0,002698 |
| 38, 62 | 0,004473 |
| 39, 61 | 0,007111 |
| 40, 60 | 0,010844 |
| 41, 59 | 0,015869 |
| 42, 58 | 0,022292 |
| 43, 57 | 0,030069 |
| 44, 56 | 0,038953 |
| 45, 55 | 0,048474 |
| 46, 54 | 0,057958 |
| 47, 53 | 0,066590 |
| 48, 52 | 0,073527 |
| 49, 51 | 0,078029 |
| 50 | 0,079589 |
Yleinen kaava w voiton todennäköisyydelle n yrityksestä, jossa jokaisen voiton todennäköisyys on p, on combin(n,w) × p w × (1-p) (nw) = [n!/(w! × (nw)!] × p w × (1-p) (nw) .
Jos heitän kolikkoa 1 000 kertaa, mikä on todennäköisyys, että näen peräkkäin vähintään 10 kruunaa tai klaavaa?
Onpa hauskaa kysyä, mutta eräs toinen lukija lähetti minulle juuri akateemisen artikkelin tästä aiheesta. Artikkelissa on seuraava kaavio, joka osoittaa todennäköisyyden olevan noin 62 %.
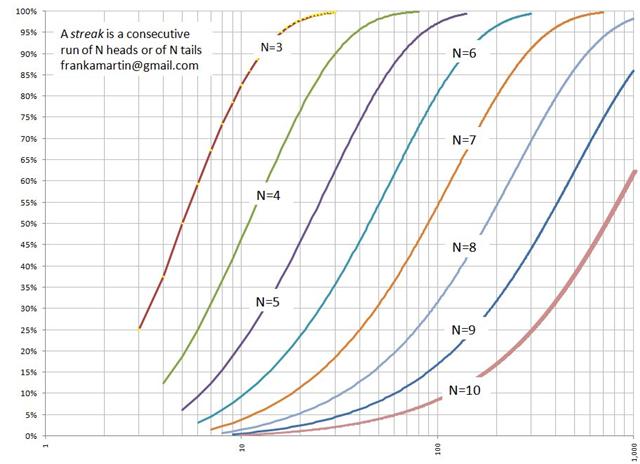
Lisätietoja tästä aiheesta on Frank Martinin kirjassa Mitkä olivat todennäköisyydet niin kauhealle kasinon putkelle? (483 kt).
Jos kolikkoa heitetään 100 kertaa, mikä on todennäköisyys saada vähintään kerran peräkkäin vähintään seitsemän kruunan putki?
Jos vastaukselle on olemassa helppo, ei-rekursiivinen lauseke, en ole siitä tietoinen. On kuitenkin olemassa helppo rekursiivinen vastaus.
f(n)= pr(ensimmäisen käännöksen hännät)×f(n-1) +
pr(krunkki ensimmäisessä käännöksessä, klaava toisessa käännöksessä)×f(n-2) +
pr(kruuna kahdessa ensimmäisessä voltissa, klaava kolmannessa voltissa)×f(n-3) +
pr(kruna kolmella ensimmäisellä heitolla, klaava kolmannella heitolla)×f(n-4) +
pr(kruna neljässä ensimmäisessä heitossa, klaava neljännessä heitossa)×f(n-5) +
pr(kruuna viidessä ensimmäisessä heitossa, klaava viidennessä heitossa)×f(n-6) +
pr(kuuden ensimmäisen heiton kruuna, kuudennen heiton klaava)×f(n-7) +
pr(pää seitsemän ensimmäisen heiton aikana) =
(1/2) × f(n-1) +
(1/2) 2 × f(n-2) +
(1/2) 3 × f(n-3) +
(1/2) 4 × f(n-4) +
(1/2) 5 × f(n-5) +
(1/2) 6 × f(n-6) +
(1/2) 7 × f(n-7) +
(1/2) 7
Jossa:
f(n) = onnistumistodennäköisyys n voltin sisällä.
pr(x) = x:n tapahtuman todennäköisyys.
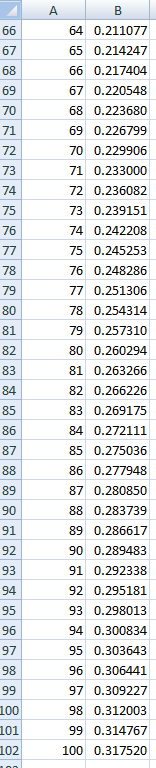
Taulukkolaskentaohjelmat sopivat täydellisesti tällaisiin ongelmiin. Alla olevissa laskentataulukon kuvakaappauksissa olen asettanut soluille B2–B8 todennäköisyydeksi 0, koska kuudessa tai vähemmässä heitossa ei voi olla seitsemää kruunaa peräkkäin. Solulle B9 olen asettanut kaavan:
=(1/2)*B8+(1/2)^2*B7+(1/2)^3*B6+(1/2)^4*B5+(1/2)^5*B4+(1/2)^6*B3+(1/2)^7*B2+(1/2)^7
Sitten kopioin ja liitin sen soluista B10 soluun B102, mikä vastaa 100 volttia. Todennäköisyys on 0,317520. Satunnainen simulaatio vahvistaa sen.
 |  |
Tämän alkuperäisen julkaisun jälkeen Rick Percy jakoi kanssani matriisialgebraratkaisunsa. Tässä se omin sanoin. Oletan, että lukija tuntee jo matriisialbegran perusteet.
Ensinnäkin, räpylä voi olla kahdeksassa mahdollisessa tilassa millä tahansa hetkellä:
p 1 = Onnistumisen todennäköisyys, olettaen, että tarvitset 7 päätä lisää nykyisestä pisteestä.
p 2 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 6 päätä.
p 3 = Onnistumisen todennäköisyys, olettaen, että tarvitset 5 kruunaa lisää nykyisestä pisteestä.
p 4 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 4 kruunaa.
p 5 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan vielä 3 kruunaa.
p 6 = Onnistumisen todennäköisyys, olettaen, että nykyisestä pisteestä tarvitaan kaksi lisäpäätä.
p 7 = Onnistumisen todennäköisyys, olettaen, että tarvitset yhden kruunan lisää nykyisestä pisteestä.
p 8 = Onnistumisen todennäköisyys, olettaen, että et tarvitse enempää päitä = 1.
Määritellään maksriksi S n todennäköisyytenä olla kussakin tilassa n :nnen käännöksen jälkeen. S 0 edustaa todennäköisyyksiä ennen ensimmäistä käännettä, jolloin on 100 %:n mahdollisuus olla tilassa 0. Joten S 0 =
| 1 0 0 0 0 0 0 0 0 |
Olkoon T kahden peräkkäisen käännöksen muunnosmatriisi eli S n > S n+1 , missä S n+1 = T × S n
- Jos olet tilassa 1, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 2 (kruuna) ja 0,5 mahdollisuus pysyä tilassa 1 (klaava).
- Jos olet tilassa 2, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 3 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 3, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 4 (ja saada kruuna) ja 0,5 mahdollisuus palata tilaan 1 (ja saada klaava).
- Jos olet tilassa 4, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 5 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 5, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 6 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 6, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 7 (kruuna) ja 0,5 mahdollisuus palata tilaan 1 (klaava).
- Jos olet tilassa 7, niin yhden voltin jälkeen sinulla on 0,5 mahdollisuus olla tilassa 8 (ja saada kruuna) ja 0,5 mahdollisuus palata tilaan 1 (ja saada klaava).
- Jos olet tilassa 8, olet saavuttanut onnistumisen ja pysyt tilassa 8 todennäköisyydellä 1,0.
Laittamalla kaikki tämä siirtymämatriisin T muotoon =
| 0,5 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,5 0,0 0,0 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,5 0,0 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 0,0 |
| 0,5 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,5 |
| 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 |
Päästäkseen kunkin tilan todennäköisyyteen yhden käännöksen jälkeen...
(1) S1 = S0 × T
Entä kahden käännöksen jälkeen?
(2) S2 = S1 × T
Sijoitetaan yhtälö (1) yhtälöön (2)...
(3) S2 = S0 × T × T = S0 × T2
Entä kolmen käännöksen jälkeen?
(4) S3 = S2 × T
Sijoittamalla yhtälö (3) yhtälöön (4)...
(5) S3 = S0 × T2 × T = S0 × T3
Voimme jatkaa tätä aina osavaltioon asti sadannen voltin jälkeen...
S 100 = S 0 × T 100
Mikä sitten on T 100 ? Ennen tietokoneita tällaisten asioiden selvittäminen on täytynyt olla valtavan hankalaa. Excelin MMULT-funktiolla ja paljon kopioimalla ja liittämällä saadaan kuitenkin T 100 =
| 0,342616 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,317520 |
| 0,339863 0,170617 0,085653 0,042999 0,021586 0,010837 0,005440 0,323005 |
| 0,334379 0,167864 0,084271 0,042305 0,021238 0,010662 0,005352 0,333929 |
| 0,323454 0,162380 0,081517 0,040923 0,020544 0,010313 0,005178 0,355690 |
| 0,301693 0,151455 0,076033 0,038170 0,019162 0,009620 0,004829 0,399038 |
| 0,258346 0,129694 0,065109 0.032686 0,016409 0,008237 0,004135 0,485384 |
| 0,171999 0,086347 0,043347 0,021761 0,010924 0,005484 0,002753 0,657384 |
| 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000 |
Oikeassa yläkulmassa oleva termi näyttää todennäköisyyden olla tilassa 8 100 voltin jälkeen, joka on 0,317520.
Oletko kuullut tarinan australialaisesta kriketinpelaajasta, joka tuomitsi kolikonheiton väärin 35 pelissä peräkkäin, ennen kuin sai 36. tuomion oikein? Mikä on sen todennäköisyys?
En ollut kuullut siitä ennen kuin mainitsit sen. Viittaat hämmästyttävään tarinaan teini-ikäisestä krikettipelaajasta, joka pelasi Magpies-joukkueessa, Kristy Perrinistä , joka todellakin arvasi kolikonheiton väärin 35 kertaa peräkkäin. Todennäköisyys saada tasan 35 tai enemmän väärin on (1/2) 35 = 1/34 359 738 368. Vertailun vuoksi Powerballin osumisen todennäköisyys on 1/195 249 054. Se on 176 kertaa todennäköisempää kuin 35 peräkkäisen kolikonheiton ohiheitto.
Onko sinulla vinkkejä kolikonheitolla lyömiseen vetoa?
Kyllä! Lyö vetoa heittäjän kädessä olevalle puolelle kuvapuoli ylöspäin. Persi Diaconisin, Susan Holmesin ja Richard Montgomeryn akateeminen artikkeli Dynamical Bias in the Coin Toss päättelee, että kolikko pysähtyy 51 %:ssa tapauksista samalle puolelle kuin se lähti heittämään.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Kuinka monta yritystä keskimäärin tarvitaan 50/50-pelissä, jotta häviää kaksi peräkkäistä yritystä? Entä 3, 4, n yritystä peräkkäin?
Ratkaistaan ensin kahden tappion tapaus.
Olkoon x odotettu tulevien volttien lukumäärä alusta alkaen tai minkä tahansa voiton jälkeen.
Olkoon y odotettu tulevien volttien lukumäärä yhden tappion jälkeen.
Voimme muodostaa seuraavat kaksi yhtälöä:
(1) x = 1 + 0,5x + 0,5y
Ykkönen tarkoittaa, että pelaajan täytyy heittää kolikkoa vaihtaakseen tilaa. On 50 %:n todennäköisyys voittaa ja pysyä tilassa x. On 50 %:n todennäköisyys hävitä ja edetä tilaan y.
(2) y = 1 + 0,5x
Jälleen tilasta y, 1 edustaa korttien kääntöä siinä vaiheessa. Voiton todennäköisyys on 50 %, minkä jälkeen palataan tilaan x. Häviön todennäköisyys on 50 %, jolloin peli päättyy eikä lisäkäännöksiä tarvita, joten implisiittinen kerroin on 0,5*0.
Kerro molemmat yhtälöt kahdella ja järjestä ne uudelleen saadaksesi:
(3) x - y = 2
(4) -x + 2y = 2
Lisää kaksi yhtälöä saadaksesi:
(5) y = 4
Syötä se mihin tahansa yhtälöön (1) - (4) ja saat x=6.
Kolmen tappion tapauksessa määrittele kolme mahdollista tilaa seuraavasti:
Olkoon x odotettu tulevien volttien lukumäärä alusta alkaen tai minkä tahansa voiton jälkeen.
Olkoon y odotettu tulevien volttien lukumäärä yhden tappion jälkeen.
Olkoon z odotettu tulevien volttien lukumäärä kahden tappion jälkeen.
Alkuperäiset yhtälöt ovat:
x = 1 + 0,5x + 0,5y
y = 1 + 0,5x + 0,5z
z = 1 + 0,5x
Voimme muotoilla alkutilat matriisimuodossa seuraavasti:
| 0,5 | -0,5 | 0 | 1 |
| -0,5 | 1 | -0,5 | 1 |
| -0,5 | 0 | 1 | 1 |
Jos muistat matriisialgebrasi, voimme ratkaista x:n muodossa determinantti(A)/determinantti(B), missä
A =
| 1 | -0,5 | 0 |
| 1 | 1 | -0,5 |
| 1 | 0 | 1 |
B =
| 0,5 | -0,5 | 0 |
| -0,5 | 1 | -0,5 |
| -0,5 | 0 | 1 |
| 0,5 | -0,5 | 0 |
| -0,5 | 1 | -0,5 |
| -0,5 | 0 | 1 |
Excelissä on kätevä determinanttifunktio: =mdeterm(alue). Tässä tapauksessa x = mdeterm(matriisi A)/mdeterm(matriisi B) = 1,75/0,125 = 14.
Voimme käyttää rekursiota peräkkäisten tappioiden lisäämiseen. Tarkastellaan kohtaa 4. Tiedämme yllä olevasta, että keskimäärin tarvitaan 14 kolikonheittoa kolmen peräkkäisen tappion saavuttamiseksi. Tässä vaiheessa kolikko käännetään uudelleen, ja 50 %:n todennäköisyydellä aloittaa alusta. Joten:
x = 14 + 1 + x/2
x/2 = 15
x = 30
Toisin sanoen, lisää yksi edelliseen vastaukseen ja sitten kaksinkertaista.
Kaavan hahmottaminen ei ole vaikeaa. Odotusarvoinen määrä voltteja n peräkkäisen tappion saavuttamiseksi on 2n +1 -2.
Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Olettaen, että reilua kolikkoa heitetään n kertaa, mikä on todennäköisyys nähdä ainakin yksi t-häntäinen putki?
Vastaus on 1-F (t) n+2 / 2n , jossa F (t) n on n:s luku t-askelisen Fibonaccin jonon sisällä.
Saatat kysyä, mikä on Fibonaccin lukujono? Ensimmäinen luku on yksi. T-askeleen lukujonossa jokainen seuraava luku on edellisen t luvun summa. Oletetaan, että mikä tahansa luku ennen ensimmäistä lukua on nolla.
Tarkastellaan kaksiaskelista lukujonoa. Ensimmäinen luku on 1. Toinen on kahden edellisen luvun summa. Oletetaan, että ykkösen edessä on nolla, joten toinen luku on 0 + 1 = 1. Kolmas luku on 1 + 1 = 2, neljäs on 1 + 2 = 3 ja viides on 2 + 3 = 5.
Ensimmäiset kaksitoista kaksiaskelista Fibonaccin lukua ovat: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
Otetaan esimerkki. Mikä on todennäköisyys saada kaksi peräkkäistä häntää ainakin kerran kymmenessä heitossa?
Käytämme kaksiaskelista Fibonaccin lukujonoa, koska tarvitsemme vain kaksi häntää. Lukujonon 12. luku (kaksi enemmän kuin volttien lukumäärä) on 144. Vastaus on siis 1 - F (2) 10 + 2 / 2 10 = 1 - 144/2 10 = 1 - 144/1024 = 85,94 %.
Entä todennäköisyys saada viisi peräkkäistä häntää 20 voltilla?
Ensimmäiset 22 viisiaskelista Fibonaccin lukua ovat 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, 26784, 52656, 103519, 203513, 400096 ja 786568.
Vastaus on siis 1 - F (5) 20 + 2 /2 20 = 1 - 786 568 / 1 048 576 = 1 - 75,01 % = 24,99 %.
Tätä kysymystä käsitellään foorumillani Wizard of Vegasissa .
Kolikko on harhainen ja sillä on 60 %:n todennäköisyys osua kruunaan. Sitä käännetään, kunnes peräkkäin tulee joko kaksi kruunaa tai kaksi klaavaa. Mikä on todennäköisyys, että ensin tulee kaksi kruunaa?
Tässä on vastaus ja ratkaisu (PDF).
Jos haluat keskustella tästä ongelmasta, käy foorumillani Wizard of Vegasissa .
Velho, haastan sinut vetoon. Tässä ovat säännöt:
- Voit valita minkä tahansa mieleisesi kuvion päistä (H) ja hännistä (T). Esimerkiksi PTT.
- Kun paljastan kuviosi, valitsen omani.
- Heitämme kolikkoa yhä uudelleen, kunnes yksi kuvio näkyy järjestyksessä. Se, joka valitsee kyseisen kuvion, voittaa.
- Annan sinulle kertoimen 3–2.
Hyväksytkö? Teen sen niin monta kertaa kuin haluat.
Ei. Hyvä yritys kuitenkin. Toisena toimivalla henkilöllä on valtava asemaetu. Tässä on toisena toimivan henkilön strategia ja hänen voittotodennäköisyytensä.
Odiusgambit-pelistrategia
| Pelaaja 1 | Pelaaja 2 | Pääpelaaja 2 voittaa |
|---|---|---|
| HHH | THH | 87,50 % |
| HHT | THH | 75,00 % |
| HTH | HHT | 66,67 % |
| HHT | THH | 75,00 % |
| THH | HTT | 75,00 % |
| THT | TTH | 66,67 % |
| TTH | HTT | 75,00 % |
| TTT | HTT | 87,50 % |
Kuten yllä oleva taulukko osoittaa, paras – tai pienin – mahdollisuuteni voittaa on valita joko THT tai HTH, jolloin voittomahdollisuuteni on silti vain 1/3. Kerroin 2:1 olisi reilu veto, joten jos saat vain 3:2, etu on 16,67 %.
Tässä on tapa muistaa toisen pelaajan strategia. Olkoon P(x) pelaajan 1 valinta pelipaikalle x. Olkoon O(x) pelaajan 1 valinnan vastakohta pelipaikalle x. Pelaajan 2 tulisi aina valita: O(2) - P(1) - P(2).
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Jos heität reilua kolikkoa 40 kertaa, mikä on todennäköisyys saada SEKÄ viiden kruunan putki että viiden klaavan putki? "Puituputki" tarkoittaa vähintään yhtä ja "5" tarkoittaa vähintään viittä. Kruunun ja häntäputken ei tarvitse olla vierekkäin.
Napsauta alla olevaa painiketta nähdäksesi vastauksen.
Tässä on ratkaisuni (PDF).
Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .
Henri ja Tom päättävät lyödä vetoa kolikonheitosta. Henri voittaa kruunalla, Tom klaavalla.
Hinta on dollari per voltti ja heillä on todella tylsää, joten he päättävät tehdä miljoona volttia. Pelin lopussa häviäjä kirjoittaa voittajalle shekin loppusaldon kattamiseksi. Mikä on shekin odotusarvo?
Vastauksen yleinen kaava on sqrt(varianssi * (2/pii)).
Tässä tapauksessa varianssi on 1 000 000. Joten odotettu absoluuttinen ero todellisten ja odotettujen tulosten välillä on sqrt(1 000 000 × (2/pi)) =~ 797,88456080286535587989211986876373695171726 232986931533185165934131585179860367700250466 781461387286060511772527036537102198390911167 448599242546125101541269054116544099863512903 269161506119450728546416733918695654340599837 28381269120656178667772134093073.
Esitän aiheeseen liittyvän kysymyksen kohdassa Kysy velholta #358 , joka auttaa näyttämään, mistä saan neliöjuuri(2/pi)-termin.
Tätä kysymystä esitettiin ja siitä keskusteltiin Wizard of Vegas -foorumilla.
Oletetaan, että kasinolla on peli, joka perustuu reiluun kolikonheittoon ja maksaa tasapelin. Pelaaja haluaa pelata miljoona kertaa 1 dollarin panoksella. Kuinka paljon rahaa hänen pitäisi tuoda pöytään, jotta hänellä olisi 50 %:n mahdollisuus olla menemättä konkurssiin?
Vastataanpa ensin kysymykseen, mikä on todennäköisyys sille, että pelaaja on tappiolla yli x yksikköä miljoonan flipin jälkeen olettaen, että pelaajalla on rajaton pelikassa.
Koska tämä on reilu veto, keskimääräinen voitto miljoonan heiton jälkeen on nolla. Kunkin heiton varianssi on 1, joten miljoonan heiton varianssi on miljoona. Yksi keskihajonta on siis sqrt(1 000 000) = 1000.
Voimme löytää tarvittavan pelikassan Excel-funktiolla =norm.inv(todennäköisyys,keskiarvo,keskihajonta). Jos esimerkiksi kirjoitamme =norm.inv(.25;0;1000), saamme -674,49. Tämä tarkoittaa, että jos miljoonan heiton jälkeen pelaajalla on 25 %:n mahdollisuus olla tappiolla 674 tai enemmän. Muista, että tämä on arvio. Saadaksemme oikean vastauksen, meidän tulisi käyttää binomijakaumaa, mikä olisi erittäin työlästä miljoonan heiton kanssa.
On hyvinkin mahdollista, että jos pelaaja ottaa pöytään 674 dollaria, hänen rahansa saattavat loppua ennen miljoonan dollarin käännettä. Jos hän pystyy jatkamaan pelaamista luotolla, hän voi toipua ja päättää pelinsä alle 674 dollarin tappiolla. Itse asiassa, kun pelaajan saldo on -674, on 50/50 mahdollisuus, että hän päätyy yli- tai alle -674 dollarin milloin tahansa tulevaisuudessa.
Joten jos pelaaja voi pelata luotolla, on olemassa kolme mahdollista lopputulosta.
- Pelaaja ei koskaan putoa alle -674:n.
- Pelaajan saldo putoaa jossain vaiheessa alle -674:n, mutta toipuu ja lopettaa pelinsä yli -674:n.
- Pelaaja putoaa jossain vaiheessa alle -674:n, jatkaa pelaamista ja häviää vielä enemmän.
Olemme todenneet, että skenaarion 3 todennäköisyys on 25 %.
Skenaariolla 2 täytyy olla sama todennäköisyys kuin skenaariolla 3, koska kun pelaaja on tappiolla -674, hänellä on 50/50 mahdollisuus sijoittua kyseisen pisteen ylä- tai alapuolelle miljoonan voltin jälkeen.
Skenaario 1 on ainoa muu vaihtoehto, jonka todennäköisyyden on oltava 100%-25%-25% = 50%.
Jos todennäköisyys sille, että pelaaja ei koskaan putoa alle 674:n, on 50 %, niin vaihtoehtona putoamiselle alle sen on oltava 100–50 % = 50 %.
Eli tässä on vastauksemme alkuperäiseen kysymykseen, 674 dollaria.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .


