WOO logo

Velho suosittelee

Todennäköisyys - Nopat

Jos heität kuutta kuusisivuista standardinoppaa, mikä on todennäköisyys saada kuutoset samanlaisia?

Jeff B. alkaen Miami, Florida

Vastaus on 6 * (1/6) 6 = 6/46 656 = 1/7 776 = ~ 0,0001286 .
Mikä on keskimääräinen heittojen määrä, kunnes heittäjä "saa seitsemän ulos"? Tiedän, että 7 ilmestyy joka kuudennen heiton välein, mutta kun otetaan huomioon come-out-7-11 ja craps-pelit sekä mahdollisuus saada useita pisteitä, uskon, että keskimääräinen heittojen määrä voi olla odotettua suurempi. Onko tästä olemassa matemaattista viitemateriaalia?

Grshooter alkaen Kansas City, Missouri

Keskimääräinen heittojen määrä heittäjää kohden on 8,525510. Tasan 2–200 heiton todennäköisyyden löydät craps-pelin selviytymistodennäköisyyssivultani .
Mitkä ovat todennäköisyydet (ja tiheys) 100 000 nopanheitossa (craps/dont pass -linja) hävitä DP-panos, jos se on 2x, 3x, 4x, 5x, 6x, 7x, 8x tai 9x peräkkäin?

Derick alkaen Minneapolis, USA

Craps-liitteeni näyttää, kuinka lasketaan yhden vedon kertoimet. Sieltä näet, että don't pass -vedon häviämisen todennäköisyys on 2928/5940. n vedon häviämisen todennäköisyys peräkkäin on (2928/5940) n . Tasan n vedon häviämisen todennäköisyys 100 000:ssa voidaan arvioida tarkasti muotoon 100 000 * (2928/5940) n+2 .
Mikä on todennäköisyys saada sama luku kuudella nopalla yhdellä heitolla?

Kyle Hill alkaen Colstrip, Montana

Todennäköisyys saada kuusi samaa numeroa kuudella nopalla on 6 * (1/6) 6 = 1/7776 = ~ 0,01286 %.
Kuinka usein voit heittää kahta noppaa 28 kertaa saamatta tulosta seiska? Miten päättelit tämän? Onnittelut sivustostasi, se on mahtava.

Arturo G. alkaen Mexico City, Mexico

Kiitos kohteliaisuudesta. Tarkoitat ilmeisesti todennäköisyyttä, että kahta noppaa heitetään 28 kertaa ilman, että saadaan 7. Todennäköisyys sille, ettei millään heitolla saada 7, on 5/6. Todennäköisyys sille, ettei 28 heitolla saada 7, on (5/6) 28 = 0,006066 eli noin 1:165.
Vain kysymys itämaisesta noppapelistä, jossa pelaajien on arvattava, kumpi puoli nopasta tulee näkyviin. Pelaajat asettavat ensin panoksensa numeroille 1, 2, 3, 4, 5 ja 6 (kuten ruletissa) ja sitten "jakaja" heittää samanaikaisesti kolmea noppaa. Voitot ovat 1:1, jos valittu numero ilmestyy kerran (millä tahansa kolmesta nopasta), 2:1, jos valittu numero ilmestyy kahdesti, ja 3:1, jos valittu numero ilmestyy kaikille kolmelle nopalle. Koska pelaaja voi asettaa minkä tahansa määrän panoksia laudalla, mikä on optimaalinen panosten määrä? (olettaen, että kaikki panokseni ovat samansuuruisia)

Jansen alkaen Toronto, Canada

Kolmen samanlaisen tuloksen todennäköisyys on 1/216. Kahden samanlaisen tuloksen todennäköisyys on 3 * 5/216. Yhden samanlaisen tuloksen todennäköisyys on 25 * 5/216. Yhden samanlaisen tuloksen todennäköisyys on 5 * 5 * 5/216. Joten odotettu tuotto on 3 * (1/216) + 2 * (15/216) + 1 * (75/216) - 1 * (125/216) = - 17/216 = - 7,87 %. Optimaalista vetojen määrää ei ole, joten menetät odotetusti 7,87 % panoksestasi riippumatta siitä, mitä teet.

Näitä vetoja voi tehdä sekä Sic Bossa että Chuck a Luckissa .
Herra velho, mikä on todennäköisyys saada kaksi paria, kun heitetään neljää noppaa?

Brian alkaen St. Catherines, Canada

On mahdollista saada combin(6,2) = 15 erilaista parijoukkoa. On mahdollista saada combin (4,2) = 6 eri tapaa, joilla noppa voi heittää mitkä tahansa kaksi paria. On 6^4 = 1296 tapaa heittää neljä noppaa. Todennäköisyys on siis 90/1296 = 6,9444 %.
Jos heitän noppaa, todennäköisyyteni saada kuutonen on 1/6. Jos heitän kahta noppaa, kasvaako todennäköisyyteni saada kuutonen toisella niistä vai pysyykö se 1/6:ssa?

Mike R. alkaen Rosemount

Jos heitit x noppaa, todennäköisyys saada ainakin yksi 6 on 1-(5/6) ^2 . Kahden nopan tapauksessa tämä on 30,56 %.
Kuinka monella eri tavalla on mahdollista heittää 3 ykköstä käyttämällä 6 noppaa?

Jamie alkaen Croydon, England

Ensin on komb (6,3)=20 tapaa, joilla voit valita kolme noppaa kuudesta kolmelle ykköselle. Sitten kukin kolmesta muusta voi olla mikä tahansa viidestä numerosta. Joten kokonaistavat ovat 20 × 5 3 = 2500. Kaikkien noppien heittotapojen kokonaismäärä on 6 6 = 46 656, joten todennäköisyys saada tasan kolme ykköstä on 2500/46656 = 0,0536. Apua komb(k)ofunktioon saat pokerin todennäköisyydet -osiostani .
Mikä on todennäköisyys sille, että yksi noppa näyttää YKSI, kun kolmea noppaa heitetään yhdessä? Ymmärtääkseni todennäköisyyden pitäisi olla 50 % (1/6 + 1/6 + 1/6 = 1/2 --> 50 %). Mutta sinun kertoimesi taulukossa se näyttää 34,72 %. Autathan.

John C. alkaen Singapore

Todennäköisyys saada tasan yksi kolmella nopalla on 3 * (5/6) 2 * (1/6) = 75/216 = 34,72 %.
Mikä on todennäköisyys saada "pari", kun heitetään neljää noppaa?

Anthony alkaen Toronto, Canada

Pari voi olla mikä tahansa kuudesta luvusta. Kaksi muuta yksittäistä numeroa voivat olla viiden muun joukossa. Joten yhdistelmiä on jo 6 * combin(5,2) = 60. Noppia on combin(4,2) = 6, joissa pari voi esiintyä. Kaksi yksittäistä numeroa voidaan järjestää kahdella tavalla. Joten parin heittämiseen on 60 * 12 = 720 tapaa. Kaikkien nopanheittotapojen kokonaismäärä on 6 4 = 1296. Todennäköisyys on siis 720/1296 = ~ 55,56 %.
Ystävälläni on baari ja hänellä on "päivän pirtelö", jossa on kymmenen noppaa Tupperware-rasiassa. Mikä on todennäköisyys saada 8/10 samaa noppaa yhdessä pirtelössä? Kiitos ajastasi.

August alkaen Oshkosh, USA

Todennäköisyys sille, että jos heität 10 noppaa ja tasan 8 numeroa on sama, on 6*combin(10,8)*(1/6) 8 *(5/6) 2 = 1/8957,952. Todennäköisyys sille, että saat vähintään 8 samaa numeroa, on 6*[combin(10,8)*(1/6) 8 *(5/6) 2 + combin(10,9)*(1/6) 9 *(5/6) + (1/6) 10 ] = 1/8569,469.
Heitin hiljattain backgammonia pelatessani neljä kertaa peräkkäin tuplana kuutoset. Mikä on todennäköisyys, että tämä tapahtuu uudelleen?

David alkaen Sunland, USA

Jokaisella uudella heitolla todennäköisyys, että seuraavat neljä heittoa ovat kaikki tuplana kuutosia, on (1/36) 4 = 1/1679616.
Mikä on todennäköisyys saada suora yhdellä viiden nopan heitolla?

Teodoro C. Deocares alkaen Dagupan, Philippines

Väliä on kaksi mahdollista: 1–5 ja 2–6. Kukin näistä väliajoista voidaan järjestää muodossa 5! = 120. Viisi noppaa voidaan heittää 6 * 5 = 7776 tavalla. Todennäköisyys on siis 2 * 120 / 7776 = 3,09 %. Tämän todennäköisyys näyttää olevan paljon suurempi heti sen jälkeen, kun laitan merkin 0 suurelle suoralle Yahtzee-pelissä.
Tasapuolista noppaa heitetään 30 kertaa. Kuinka monta kertaa numero 1 todennäköisesti tulee ulos? Mikä on todennäköisyys, että numero 1 tulee ulos odotetun määrän kertoja?

anonyymi

Ykkösten odotettu määrä on 30 * (1/6) = 5. Todennäköisyys sille, että ykkösiä on tasan 5, on combin(30,5) * (1/6) 5 * (5/6) 25 = 19,21 %.
Jos minulla on tietty määrä noppaa, mikä on todennäköisyys, että jos heitän ne kaikki, ainakin yksi osuu ykköseen?

anonyymi

Todennäköisyys sille, että kaikki nopat eivät ole ykkösiä, on (5/6) n . Joten todennäköisyys sille, että ainakin yksi noppa on ykkönen, on 1-(5/6) n . Otetaan esimerkki viidestä noppaa. Vastaus olisi 1-(5/6) 5 = 59,81 %.
Jos heitän 36 noppaa, mikä on todennäköisyys saada ainakin yksi kuutos?

anonyymi

1-(5/6) 36 = 99,86 %
Jos jatkaisin heittämistä ja poistaisin kaikki kuutoset joka kerta, miten ennustaisin jäljellä olevien noppien teoreettisen määrän tietyn heittokertojen jälkeen?

anonyymi

Jokaisella heitolla odotetaan, että 5/6 nopista jää jäljelle. Joten n heiton jälkeen jäljellä olevien noppien odotettu lukumäärä olisi 36 * (5/6) n . Esimerkiksi 10 heiton jälkeen sinulla olisi keskimäärin 5,81 noppaa jäljellä.
Jos heitän kolme noppaa, mikä on todennäköisyys saada ainakin kaksi samaa numeroa?

anonyymi

Todennäköisyys sille, että kaikki luvut ovat erilaisia, on (5/6) * (4/6) = 20/36. Joten todennäköisyys sille, että ainakin kaksi lukua on sama, on 1-(20/36) = 16/36 = 44,44 %.
Jos kaksi ihmistä heittää noppaa, mikä on todennäköisyys sille, että ne ovat sama luku? Onko olemassa kaavaa tämän selvittämiseksi?

anonyymi

Kyllä. Lasket yksinkertaisesti läpi kaikki yhteissummat 2:sta 12:een ja määrität todennäköisyyden, että jokainen heitetään kahdesti. Vastaus olisi siis (1/36) 2 + (2/36) 2 + (3/36) 2 + (4/36) 2 + (5/36) 2 + (6/36) 2 + (5/36) 2 + (4/36) 2 + (3/36) 2 + (2/36) 2 + (1/36) 2 = 11,27 %.
Osallistuin hiljattain sairaalan juhlallisuuksiin. Palkinnoksi oli uusi auto, jos seitsemän noppaa sai seitsemän kuutosen yhdellä heitolla. 1,00 puntaa per heitto. Kertoimet tähän ovat varmasti korkeat, mutta kuinka korkeat?

anonyymi

Todennäköisyys saada seitsemän kuutosen arvoinen tulos seitsemällä nopalla on (1/6) 7 = 1/279 936. Auton arvon pitäisi siis olla 279 936 puntaa tai enemmän, jotta tämä olisi hyvä veto. Edes tavallinen Rolls Royce ei ole näin paljon arvoinen, joten sanoisin, että se oli huono veto.

[Bluejay lisää: Öö, joo, mutta mielestäni pointti oli, että se oli hyväntekeväisyyteen. Kumpi on hauskempaa: Lahjoittaa 1,00 puntaa hyväntekeväisyyteen ja saada vastineeksi vain hyvän auttamisen tunteen vai lahjoittaa 1,00 puntaa ja saada hyvä tunne sekä pieni mahdollisuus voittaa auto?]

Mitkä ovat todennäköisyydet sille, että viiden nopan heitolla saadaan viitos, neloset, kolmoset, täyskäsi, kakkospari, pari, suora ja ei yhtään?

anonyymi

  • Viisi samaa: 6/6 5 = 0,08 % (ilmeinen)
  • Neloset: 5 * 6 * 5 = 1,93 % (viisi mahdollista sijoitusta nelosille * 6 sijoitusta nelosille * 5 sijoitusta singletonille).
  • Täyskäsi: combin(5,3)*6*5/6 5 = 3,86 % (combin(5,3) positiot kolmosille * 6 arvoa kolmosille * 2 arvoa parille).
  • Kolmoset: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 6 5 = 15,43%. (combin(5,3) sijat kolmosille * combin(2,1) sijat suuremmalle yksittäisistä korteista * 6 kolmosten arvoa * combin(5,2) sijat kahdelle yksittäiselle kortille.
  • Kaksi paria: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 6 5 = 23,15 % (combin(5,2) sijat korkeammalle parille * combin(3,2) sijat alemmalle parille * combin(6,4) sijat kahdelle parille * 4 sijaa singletonille).
  • Pari: COMBIN(5,2)*fact(3)*6*combin(5,3) / 6 5 = 46,30 % (combin(5,2) positiot parille * fact(3) positiot kolmelle yksittäiselle alkiolle * 6 sijoitusta parille * combin(5,3) sijoitusluvut yksittäisille alkioille).
  • Suora: 2*fact(5) / 6 5 = 3,09 % (2 väliä suoralle {1-5 tai 2-6} * fact(5) järjestyksen järjestämistavalle).
  • Ei mitään: ((COMBIN(6,5)-2)*FACT(5)) / 6 5 = 6,17% (combin(6,5) tapaa valita 5 arvoa kuudesta, vähennettynä 2 suorille, * fact(5) tapaa järjestää järjestys.
Hei velho, haluaisin tietää, voitko vastata tähän. 1600-luvun Ranskassa suositussa uhkapelissä pelaaja heitti noppaa 24 kertaa. Hän voitti panoksensa, jos ainakin toinen näistä heitoista oli tuplana kuusi. Tuolloin keskusteltiin siitä, oliko voittotodennäköisyys yli vai alle parillisen 50 %. Voitko auttaa minua?

anonyymi

Toki, tämä on helppoa. Todennäköisyys saada ainakin yksi 12 24 heitolla on 1-(35/36) 24 = 49,14%. Kertoimet siis puoltavat 12:ta vastaan panostamista. Tämä on fiksu veto, koska odotettu kahdentoista määrä 24 heitolla on 2/3. Se ei kuitenkaan tarkoita, että 12:n todennäköisyys olisi 2/3, koska joskus 12:ia tulee useampi kuin yksi, eikä 12:lle panostanut pelaaja voita enää ylimääräisten kahdentoista jälkeen ensimmäisen yrityksen jälkeen. Jos minkä tahansa yrityksen voittamisen todennäköisyys on p, yritysten lukumäärä on n ja ainakin yhden voiton todennäköisyys on w, niin n:n ratkaiseminen p:n ja w:n avulla antaa meille...

w=1-(1-p) n
1-w = (1-p) n
log(1-w) = log((1-p) n )
log(1-w) = n * log(1-p)
n = log(1-w) / log(1-p)

Esimerkissäsi n = log(1-0,5) / log(1-(1/36)) = log(0,5) / log(35/36) = 24,6051. Jos siis onnistumistodennäköisyys on 50 % 24,6 heitolla, sen täytyy olla hieman pienempi 24 heitolla.

Mikä on todennäköisyys, että kuudella nopalla heitetään kuusi kertaa peräkkäin lukuja 1, 2, 3, 4, 5 ja 6?

anonyymi

Todennäköisyys sille, että kuudella nopalla heitetään luku 123456 yhdellä heitolla, voidaan ilmaista muodossa tod(toinen noppa ei osu ensimmäiseen noppaan) * tod(kolmas noppa ei osu ensimmäiseen eikä toiseen noppaan) * ... = 1*(5/6)*(4/6)*(3/6)*(2/6)*(1/6) = 0,015432. Joten todennäköisyys sille, että tämä tehdään kuusi kertaa peräkkäin, on 0,015432 * 6 = 1/74 037 208 411.
Jos heitän yhtä noppaa kuusi kertaa, mikä on todennäköisyys saada "2" tasan neljä kertaa?

anonyymi

Yhdistä(6,2)*(1/6) 4 *(5/6) 2 = 0,008037551.
Mikä on todennäköisyys saada 3, 4 ja 5 nopalla tulos 13 tai enemmän, jos saat pitää kolme korkeinta noppaarvoa heitossasi?

anonyymi

Tässä ovat todennäköisyydet:

3 noppaa: 25,93 %
4 noppaa: 48,77 %
5 noppaa: 66,13 %.

Oletetaan, että heitämme kolme reilua kuusisivuista noppaa. Mikä on ehdollinen todennäköisyys sille, että ensimmäinen noppa näyttää lukua 4, kun kaikkien kolmen heitetyn luvun summa on 12?

Shikha alkaen North Ryde

Todennäköisyys sille, että A heitetään tietyllä B:llä, on A:n ja B:n todennäköisyydet jaettuna B:n todennäköisyydellä. Tässä tapauksessa todennäköisyys sille, että ensimmäisellä nopalla saadaan 4 ja kahdella muulla yhteensä 8, on (1/6)*(5/36) = 5/216. Todennäköisyys sille, että kolmella nopalla saadaan yhteensä 12, on 25/216, kuten sic bo -osiossani on esitetty. Joten vastaus on (5/216)/(25/216) = 5/25 = 20 %.
Äskettäisessä ohjelmointiharjoituksessa minua ja muita opiskelijoita pyydettiin kuvailemaan kuusisivuinen noppa koodilla ja sitten käyttämään noppaamme yksinkertaisen pelin määrittämiseen. Pelin tavoitteena oli heittää noppaa, kunnes heittojen summa oli tasan 100. Yli 100:n heittoja ei lisätty yhteen, vaan ne lisättiin tilastoihin. Nopeasti määritettiin, että 17 heittoa olisi pienin tarvittava heittomäärä 100:n saavuttamiseksi. Tämän toteutumisen todennäköisyyden laskeminen on kuitenkin osoittautunut vaikeaksi. Tietyn heittosarjan todennäköisyyden laskeminen on melko suoraviivaista, mutta miten voisi ottaa huomioon sekä heittojen epämääräisen järjestyksen että erilaiset tavat saavuttaa 100 17 heitolla (16 * 6 + 1 * 4 ja 15 * 6 + 2 * 5)?

Björn alkaen Göteborg, Sweden

Mainitsemasi kaksi tapaa ovat ainoat tavat heittää yhteensä 100 pistettä 17 heitolla. Todennäköisyys saada 16 kuutosen ja yksi nelosen on 17*(1/6) 17 . Nelosen heittopaikkoja on 17 ja jokaisen sekvenssin todennäköisyys on (1/6)*(1/6)*...*(1/6) 17 termillä. Tapojen lukumäärä 15 kuutosen ja 2 viitosen saamiseksi on yhteensä (17,2) = 136. Joten 15 kuutosen ja 2 viitosen todennäköisyys on 136*(1/6) 17 . Joten kokonaistodennäköisyys on (17+136)*(1/6) 17 . = 1/110 631 761 077.
Noppia on kolme. Kaksi niistä on oikeita kuusisivuisia noppia ja yksi on noppa, jonka kaikki sivut sisältävät kuutonen. Kaikki nopat ovat taskussani. Otan satunnaisesti nopan ja heitän sen. Tulos on 6. Mikä on todennäköisyys, että noppa oli yksi oikeista nopista, joilla oli kuusi eri arvoa?

Annojh alkaen Toronto

Olkoon A = Normaalin nopan valinta
Olkoon B = Heitetään 6 satunnaisesti valitulla nopalla
Vastaus = Pr(A annettuna B) = Pr(A ja B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.
Jos voit heittää kuutta noppaa vain kerran, mikä on todennäköisyys sille, että saat 6, 6, 6, 6, 1 ja 4 missä tahansa järjestyksessä?

Aubrey alkaen Kokomo

Näitä lukuja voi järjestää mihin tahansa järjestykseen 6!/(4!*1!*1!) = 30 tavalla. Toinen tapa ajatella asiaa on, että ykköselle on 6 paikkaa ja 4:lle 5 paikkaa, joten 6*5=30. Todennäköisyys saada luku 666614 täsmälleen tässä järjestyksessä on 1/6 = 6 = 1/46656. Kerro tämä 30:llä saadaksesi 30 mahdollista järjestystä, jolloin vastaus on 30/46656 = 0,0643 % eli 1/1552,2.
Ymmärtääkseni tapahtuman "odotusaika" on kyseisen tapahtuman todennäköisyyden käänteisluku. Olen kiinnostunut laskemaan odotusajan peräkkäisten kakkosten heittämiseen yhdellä nopalla. Simulaatiossa saan keskimäärin 42 heittoa. Miten teen yhteyden peräkkäisten kakkosten heittämisen todennäköisyyteen?

Lee alkaen Andover

On totta, että yksittäisten tapahtumien kohdalla, jos todennäköisyys on p, niin keskimääräinen odotusaika on 1/p. Peräkkäisten tapahtumien kohdalla tilanne kuitenkin monimutkaistuu. Olkoon x tila, jossa viimeinen heitto ei ollut kaksi. Tämä on myös tila alussa. Olkoon y tila, jossa viimeinen heitto oli kaksi. Ensimmäisen heiton jälkeen on 5/6 mahdollisuus, että olemme edelleen tilassa x, ja 1/6 mahdollisuus, että olemme tilassa y. Olkoon Ex(x) odotettu heittojen lukumäärä tilasta x ja Ex(y) odotettu heittojen lukumäärä tilasta y. Sitten...

Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), ja
Ex(y) = 1 + (5/6) * ex(x)

Ratkaisemalla nämä kaksi yhtälöä...

Esim.(x) = 1 + (5/6)*esimerkki(x) + (1/6)*(1 + (5/6)*esimerkki(x))
Ex(x) = 7/6 + (35/36) * Ex(x)
(1/36) * Ex(x) = 7/6
Esim.(x) = 36 * (7/6) = 42

Joten kahden peräkkäisen kakkosheiton keskimääräinen odotusaika on 42 rullaa.

Minulla on samanlainen ongelma, vain odotetut voltit kahden pään saamiseksi, matemaattisten tehtävien sivustollani, katso tehtävä 128.

Voitko kertoa minulle, mikä on todennäköisyys heittää kaksi samaa numeroa kahdella, kolmella ja neljällä nopalla? Mietin, kuinka monta noppaa pitäisi heittää kerralla, jotta todennäköisyys olisi nopan heittäjän puolella. (Sillä ei ole väliä, kumpi numero kaksinkertaistetaan.)

Mary alkaen Minneapolis, MN

Tässä on todennäköisyys saada ainakin yksi numero useammin kuin kerran heittojen lukumäärän mukaan:

Parin tai useamman todennäköisyys

Rullat Todennäköisyys
2 rullaa 16,67 %
3 rullaa 44,44 %
4 rullaa 72,22 %
5 rullaa 90,74 %
6 rullaa 98,46 %

Joten jos varaat tämän, sinun pitäisi tarjota joko kyllä, jos tilaat kolme rullaa, tai ei, jos tilaat neljä rullaa.
Mikä on mahdollisuus saada yli 100:n summa 20 noppaa heitettäessä? Ystävällisin terveisin

Terje alkaen Stockholm

Aloin käyttää normaaliapproksimaatiota tämän ratkaisemiseksi, mutta yli 100 pisteen todennäköisyys on liian pieni, jotta menetelmä olisi tarkka. Niinpä tein satunnaisen simulaation 8,25 miljoonasta yrityksestä, ja polkuja, joissa oli 101 pistettä tai enemmän, oli 127. Todennäköisyys on siis noin 1/65 000.
Velho, voisitko kuvailla Kalifornian SuperLotto Plus -arvonnan (1/41,4 miljoonaa) vastaavaa todennäköisyyttä peräkkäisten 7- tai 11-heittojen lukumääränä? Kuulin sen jossain aiemmin. Useimmat ihmiset eivät ymmärrä lottovoittoja. Mutta nopanheitto – he voivat samaistua siihen.

Tim alkaen Belmont, CA

Olkoon vastauksesi n. Todennäköisyys saada luku 7 tai 11 on 8/36. Ratkaise n seuraavasti:

(8/36) n = 1/41 400 000

log((8/36) n ) = log(1/41 400 000)

n × log(8/36) = log(1/41 400 000)

n = log(1/41 400 000)/log(8/36)

n = -7,617 / -0,65321

n = 11,6608

Eli siinä se, SuperLotto-voiton todennäköisyys on sama kuin seitsemän tai yksitoista peräkkäisen nopan heittäminen, eli 11,66 kertaa. Niille, jotka eivät ymmärrä keskeneräistä heittoa, muotoilisin ajatuksen uudelleen siten, että todennäköisyys on 11 ja 12 peräkkäisen nopan heiton välillä.

Meillä on työntekijöiden välillä erimielisyyttä. Kadun varrella on baari, jossa on yksi pirtelö päivässä. Siinä sinun täytyy heittää viisi noppaa kerralla ja kaikkien viiden on oltava samanlaisia "kuten Yahtzeessa", mutta saat kolme mahdollisuutta. Mutta sinun on poimittava kaikki nopat kaikki kolme kertaa. Joten kysymys kuuluu, mitkä ovat todennäköisyydet onnistua yhdellä piristyksellä ja mitkä ovat todennäköisyydet onnistua kolmella sallitulla piristyksellä. Kiitos, jos olet jo vastannut tähän aiemmin, olen pahoillani, mutta en löytänyt sitä.

Dan and co workers at maple island alkaen Forest Lake

Todennäköisyys saada viitoset yhdellä heitolla on 6 * (1/6) 5 = 1/1 296. Tämä johtuu siitä, että viitosia on kuusi erilaista (yhdestä kuuteen) ja todennäköisyys sille, että jokainen noppa saa kyseisen luvun, on (1/6). Todennäköisyys sille, ettei saa viitosia, on 1-(1/1 296) = 1 295/1 296. Todennäköisyys sille, että kolme yritystä ei saa kolmosta, on (1 295/1 296) 3 = 99,77 %. Joten todennäköisyys saada ainakin yksi viitos kolmella yrityksellä on 100 % - 99,77 % = 0,23 %.
Mikä on odotettu heittojen määrä, jotta saadaan ainakin yksi jokaisesta mahdollisesta tuloksesta puolueettomalla kuusisivuisella nopalla?

Michael alkaen Melbourne

Jos jonkin todennäköisyys on p, niin keskimäärin tarvitaan 1/p yritystä, ennen kuin se tapahtuu ensimmäisellä heitolla. Ensimmäisellä heitolla tietenkin yliviivaat yhden luvun. Todennäköisyys sille, että seuraavaksi heitetään jokin viidestä muusta luvusta, on 5/6. Joten keskimäärin tarvitaan 1/(5/6)=6/5=1,2 heittoa, jotta se tapahtuisi. Tätä päättelyä jatkaen loppuun asti, odotettu heittojen lukumäärä on (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14,7.
Mikä on klassinen todennäköisyys saada yhteensä 12, kun heitetään viisi tasapainoista noppaa?

Kennith H. alkaen Winters

Toivottavasti olet tyytyväinen, lisäsin juuri uuden osion , jossa vastataan tällaisiin kysymyksiin 1–25 nopalla. Kuten viiden nopan taulukko osoittaa, todennäköisyys saada yhteensä 12 on 0,039223251028807.

Jos kahta noppaa heitetään yhä uudelleen ja uudelleen, kunnes jompikumpi seuraavista tapahtumista tapahtuu, kumpi todennäköisemmin tapahtuu ensin:

  • Yhteensä heitetään kuusi ja kahdeksan, kummassakin järjestyksessä, ja kaksoiskappaleet sallitaan.
  • Yhteensä seitsemän heitetään kahdesti.

Joku tarjosi minulle vetoa siitä, että ensin osuvat kuusi ja kahdeksan. Hyväksyin vedon, koska seitsemän on todennäköisin summa. Hävisin kuitenkin 2 500 dollaria tekemällä tätä yhä uudelleen ja uudelleen. Mitkä ovat kertoimet?

Anthony alkaen Indiana

Pelkäänpä, että sait tämän vedon neliösivun. Todennäköisyys sille, että heitetään kaksi seiskaa ennen kuutosta ja kahdeksikkoa, on 45,44 %. Tässä ovat kaikki mahdolliset lopputulokset. Ensimmäinen sarake on harkitsevien heittojen järjestys vedon lopputulokseen, jättäen kaikki muut huomiotta.

Kaksi seiskaa ennen kuutos- ja kahdeksikkopanosta

Relevant Rolls Todennäköisyys Kaava Tulokset
6,8 0.142045 (16.5.)*(11.5.) Menettää
8,6 0.142045 (16.5.)*(11.5.) Menettää
6,7,8 0,077479 (16.5.)*(11.6.)*(11.5.) Menettää
7,6,8 0,053267 (16.6.)*(16.5.)*(11.5.) Menettää
8,7,6 0,077479 (16.5.)*(11.6.)*(11.5.) Menettää
7,8,6 0,053267 (16.6.)*(16.5.)*(11.5.) Menettää
7,7 0,140625 (16.6.)*(16.6.) Voittaa
6,7,7 0,092975 (16.5.)*(11.6.)*(11.6.) Voittaa
8,7,7 0,092975 (16.5.)*(11.6.)*(11.6.) Voittaa
7,6,7 0,06392 (16.6.)*(16.5.)*(11.6.) Voittaa
7,8,7 0,06392 (16.6.)*(16.5.)*(11.6.) Voittaa

Pohjimmiltaan syy siihen, miksi 6 ja 8 ovat parempi puoli, on se, että voit osua näihin numeroihin kummassa tahansa järjestyksessä: 6 ja sitten 8 tai 8 ja sitten 6. Kahdella seiskalla on vain yksi järjestys, 7 ja sitten toinen 7.

Kaksi kysymystä, kiitos: 1) Mikä on todennäköisyys saada (6)-sivuisella nopalla kerrallaan tulokseksi 6,6,6,6,6,6? 2) Mikä on todennäköisyys saada (6)-sivuisella nopalla kerralla tulokseksi 1,2,3,4,5,6? Kiitos! Se tappaa minut!

Heather alkaen Petaluma

Kuuden kuutonen todennäköisyys on (1/6) * 6 = 1 luvussa 46656. Lukujen 1, 2, 3, 4, 5, 6 heittämisen todennäköisyys kuudella nopalla on 6 ! /6 * 6 = 1 luvussa 64,8.
Mikä on todennäköisyys saada jokin luku useammin kuin kerran, jos heität noppaa kymmenen kertaa?

Ryan alkaen Silay

1-(5/6) 10 -10 × (1/6) × (5/6) 9 = 51,55 %.
Pelissä nimeltä Verotus ja veronkierto pelaaja heittää kahta noppaa. Jos minkä tahansa heiton summa on 7, 11 tai 12, pelaajaa verotetaan; minkä tahansa muun heiton yhteydessä hän välttää verot. Jos pelaaja heittää parin viisi kertaa, mikä on todennäköisyys, että hän välttää verot?

George P. alkaen Stevens Point, WI

Todennäköisyys saada luku 7, 11 tai 12 on (6+2+1)/36 = 9/36 = 1/4. Katso osiostani nopan todennäköisyyden perusteet , miten päädyin tähän lukuun. Todennäköisyys saada jokin muu on 3/4. Todennäköisyys sille, että heitetään viisi noppaheittoa ilman, että saadaan lukua 7, 11 tai 12, on (3/4) 5 = 23,73 %.
Kuinka monta nopanheittoa tarvitaan ennen kuin on todennäköistä, että olet heittänyt numerot 1, 2, 3, 4, 5 ja 6 ainakin kerran kutakin? Onko ideoita tämän yleistämiseksi n-sivuiselle nopalle?

Asif alkaen Columbia, SC

Ei niin, että kysyit, mutta käsittelen ensin keskiarvoa. Kuusisivuisella nopalla odotettu heittojen määrä, jotta jokainen sivu saadaan ainakin kerran, on (6/6) + (6/5) + (6/4) + (6/3) + (6/2) + (6/1) = 14,7. N-sivuisella nopalla odotettu heittojen määrä on (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n. Vaadittavien heittojen mediaanimäärä on 13. Todennäköisyys sille, että saadaan 13 tai vähemmän heittoja, on 51,4 % ja todennäköisyys sille, että saadaan 13 tai enemmän heittoja, on 56,21 %.
Tiedän, että olet skeptinen nopanheiton suhteen. Olen harjoitellut nopanheittoa ja hallittua heittoa kolme kuukautta. Mikä on todennäköisyys heittää 78 seiskaa 655 satunnaisella heitolla? Kiitos avusta :)

Eric B. alkaen Boston, MA

Suurille heittomäärille voimme käyttää Gaussin käyrän approksimaatiota. Odotusarvo seiskojen määrälle 655 heitolla on 655 × (1/6) = 109,1667. Varianssi on 655 × (1/6) × (5/6) = 90,9722. Keskihajonta on sqr(90,9722) = 9,5379. Saat 78 seiskaa 109,1667 − 78 = 31,1667 vähemmän kuin odotusarvo. Tämä on (31,1667 - 0,5) / 9,5379 = 3,22 keskihajontaa odotusarvoa pienemmäksi. Todennäköisyys sille, että jäädään 3,22 tai enemmän keskihajontaa odotusarvoa etelämmäksi, on 0,000641 eli 1/1 560. Sain tämän luvun Excelissä käyttämällä kaavaa normsdist(-3,22).
Tämä koskee nopanheiton hallintaa Craps-pelissä. Keskustelit aiemmin Stanford Wongin kokeesta ja totesit: "Vedonlyöntiehdot olivat, pystyisivätkö tarkkuusheittäjät heittämään alle 79,5 seiskaa 500 nopanheitolla. Satunnaispelissä odotettu luku olisi 83,33. Todennäköisyys saada 79 tai vähemmän seiskaa 500 satunnaisella heitolla on 32,66 %.... Todennäköisyys saada 74 tai vähemmän seiskaa 500 satunnaisella heitolla on 14,41 %."

Kysymykseni tästä vedosta on, että 14,41 % ei vieläkään ole "tilastollisesti merkitsevä" [eli p < 0,05], jolla yleensä tarkoitetaan suurempaa kuin kahta keskiarvosta mitattua keskihajontaa – tai todennäköisyyttä, että tapahtuma tapahtuu satunnaisesti alle 5 % sarjan *yhteensä* jommassakummassa päässä.

Kuinka monta seiskaa pitäisi heittää 500 heitolla, ennen kuin voitaisiin sanoa, että on alle 2,5 %:n todennäköisyys sille, että tulos oli täysin satunnainen (eli että tulos oli tilastollisesti merkitsevä)?

Paljon kiitoksia & muuten, sinun sivustosi on EHDOTTOMASTI PARAS löytämäni uhkapelikertoimiin ja -todennäköisyyksiin keskittyvä verkkosivusto... jatkakaa hyvää työtä!!!

Plexus alkaen Warwick, Rhode Island

Kiitos ystävällisistä sanoistasi. Sinun ei pitäisi sanoa, että todennäköisyys sille, että heitot eivät olleet satunnaisia, on p. Oikeammin se pitäisi muotoilla niin, että todennäköisyys sille, että satunnainen peli tuottaa tällaisen tuloksen, on p. Kukaan ei odottanut 500 heiton todistavan tai kumoavan mitään. En minä asettanut rajaa 79,5 seiskaan, mutta epäilen, että se valittiin tilastollisesti merkitseväksi; pikemminkin epäilen, että se oli piste, jossa molemmat osapuolet suostuivat vetoon.

2,5 %:n merkitsevyystaso on 1,96 keskihajontaa odotuksesta. Tämä voidaan löytää Excelissä kaavalla =normsinv(0,025). 500 heiton keskihajonta on sqr(500*(1/6)*(5/6)) = 8,333. Joten 1,96 keskihajontaa on 1,96 * 8,333 = 16,333 heittoa odotuksesta etelään. Odotettu seiskojen määrä 500 heitolla on 500*(1/6) = 83,333. Joten 1,96 keskihajontaa tästä etelään on 83,333 − 16,333 = 67. Binomijakaumalla tarkistetaan, että 67 seiskan tai vähemmän todennäköisyys on 2,627 %.

Kuinka monta heittoa odotetaan tarvittavan Yahtzeen saamiseksi?

Ian F. alkaen Provo

Olettaen, että pelaajalla on aina eniten edustettuna oleva numero, keskiarvo on 11,09. Tässä on taulukko, joka näyttää heittojen lukumäärän jakauman 82,6 miljoonan yrityksen satunnaissimulaatiossa.

Yahtzee-kokeilu

Rullat Esiintymiset Todennäköisyys
1 63908 0.00077371
2 977954 0.0118396
3 2758635 0,0333975
4 4504806 0,0545376
5 5776444 0,0699327
6 6491538 0,0785901
7 6727992 0,0814527
8 6601612 0,0799227
9 6246388 0,0756221
10 5741778 0,0695131
11 5174553 0,0626459
12 4591986 0,0555931
13 4022755 0.0487016
14 3492745 0,042285
15 3008766 0,0364257
16 2577969 0.0312103
17 2193272 0,0265529
18 1864107 0,0225679
19 1575763 0,019077
20 1329971 0.0161013
21 1118788 0,0135446
22 940519 0.0113864
23 791107 0.00957757
24 661672 0.00801056
25 554937 0,00671837
26 463901 0.00561624
27 387339 0.00468933
28 324079 0,00392347
29 271321 0,00328476
30 225978 0.00273581
31 189012 0.00228828
32 157709 0.00190931
33 131845 0.00159619
34 109592 0.00132678
35 91327 0.00110565
36 76216 0.00092271
37 63433 0.00076795
38 52786 0.00063906
39 44122 0.00053417
40 36785 0.00044534
41 30834 0.00037329
42 25494 0.00030864
43 21170 0.0002563
44 17767 0.0002151
45 14657 0.00017745
46 12410 0.00015024
47 10299 0.00012469
48 8666 0.00010492
49 7355 0.00008904
50 5901 0.00007144
51 5017 0.00006074
52 4227 0.00005117
53 3452 0.00004179
54 2888 0.00003496
55 2470 0.0000299
56 2012 0.00002436
57 1626 0.00001969
58 1391 0.00001684
59 1135 0.00001374
60 924 0.00001119
61 840 0.00001017
62 694 0.0000084
63 534 0.00000646
64 498 0.00000603
65 372 0.0000045
66 316 0.00000383
67 286 0.00000346
68 224 0.00000271
69 197 0.00000238
70 160 0.00000194
71 125 0.00000151
72 86 0.00000104
73 79 0.00000096
74 94 0.00000114
75 70 0.00000085
76 64 0.00000077
77 38 0.00000046
78 42 0.00000051
79 27 0.00000033
80 33 0.0000004
81 16 0.00000019
82 18 0.00000022
83 19 0.00000023
84 14 0.00000017
85 6 0.00000007
86 4 0.00000005
87 9 0.00000011
88 4 0.00000005
89 5 0.00000006
90 5 0.00000006
91 1 0.00000001
92 6 0.00000007
93 1 0.00000001
94 3 0.00000004
95 1 0.00000001
96 1 0.00000001
97 2 0.00000002
102 1 0.00000001
Kokonais 82600000 1
Tarkastellaan hypoteettista peliä, joka perustuu nopan heittoon. Jos noppa pysähtyy lukuun 1, pelaaja menettää 1 dollarin ja peli päättyy. Jos noppa pysähtyy mihin tahansa muuhun, pelaaja voittaa 1 dollarin. Tässä vaiheessa pelaaja voi antaa nopan olla heittämättä tai lopettaa. Pelaaja voi jatkaa pelaamista ja tuplata jokaisen panoksen, kunnes hän häviää tai lopettaa. Mikä on paras strategia?

Byron P. alkaen Newington, CT

Jos puhutaan vain odotusarvon maksimoinnista, pelaajan tulisi pelata ikuisesti. Vaikka todennäköisyys sille, että pelaaja lopulta häviää, on 1, missä tahansa päätöksentekopisteessä odotusarvo suosii aina uudelleen pelaamista. Tämä vaikuttaa paradoksilta. Vastaus piilee siinä, että joillakin tapahtumilla on todennäköisyys 1, mutta ne eivät silti välttämättä tapahdu. Esimerkiksi jos heitäisit tikkaa lukusuoraan 0-10, todennäköisyys sille, ettei piitä osu täsmälleen, on 1, mutta se voi silti tapahtua.

Käytännössä on kuitenkin olemassa jokin pysähdyskohta. Tämä johtuu siitä, että rahan tuoma onnellisuus ei ole verrannollinen sen määrään. Vaikka yleisesti hyväksytään, että enemmän rahaa tuo enemmän onnellisuutta, mitä rikkaammaksi tulet, sitä vähemmän onnellisuutta jokainen lisäeuro tuo sinulle.

Uskon, että hyvä tapa vastata tähän kysymykseen on soveltaa ongelmaan Kellyn kaavaa . Kellyn mukaan pelaajan tulisi tehdä jokainen päätös tavoitteenaan maksimoida pelikassansa odotettu logaritmi panoksen jälkeen. Lyhyesti sanottuna (jätin paljon matematiikkaa pois), pelaajan tulisi jatkaa tuplaamista, kunnes panos ylittää 96,5948 % hänen kokonaisvarallisuudestaan. Varallisuus tulisi määritellä voitetun summan ja pelaajan ennen ensimmäistä panosta olleiden rahojen summana. Esimerkiksi, jos pelaajalla oli aluksi 100 000 dollaria, hänen tulisi jatkaa tuplaamista 23 kertaan asti, kunnes voitto on 4 194 304 dollaria. Tässä vaiheessa pelaajan kokonaisvarallisuus on 4 294 304 dollaria. Häntä pyydetään panostamaan 4 194 304/4 294 304 = 96,67 % hänen kokonaisvarallisuudestaan, mikä on suurempi kuin 96,5948 %:n lopetuspiste, joten hänen tulisi lopettaa.

Pelaajat A ja B heittävät kahta noppaa. Pelaaja A voittaa, jos hän heittää yhteensä 6 ennen kuin B heittää yhteensä 7, ja B voittaa, jos hän heittää 7 ennen kuin A heittää 6. Jos A aloittaa, osoita, että A:n voittomahdollisuudet ovat 30/61.

Sangeeta alkaen Mumbai, India

Olkoon vastaus tähän kysymykseen p. Todennäköisyys sille, että heitetään yhteensä kuusi, on 5/36 ja todennäköisyys sille, että heitetään yhteensä seitsemän, on 6/36. Jos et ymmärrä miksi, katso osiot nopan todennäköisyyden perusteista . Voimme määritellä p:n seuraavasti:

p = Tod.(ensimmäisellä heitolla 6) + Tod.(ensimmäisellä heitolla ei 6)*Tod.(toisella heitolla ei 7)*p.

Tämä johtuu siitä, että jos kumpikaan pelaaja ei voita kahden ensimmäisen heiton jälkeen, peli palaa alkuperäiseen tilaan ja pelaajan A voittotodennäköisyys pysyy samana.

Joten meillä on:

p = (5/36) + (31/36) × (30/36) × p
p = 5/36 + (930/1296) × p
p * (1-(930/1296)) = 5/36.
p * (366/1296) = 5/36
p = (5/36) × (1296/366) = 30/61.

Kuinka monella tavalla on mahdollista heittää n kuusisivuista, ei-erillistä noppaa? Kuten todettiin, nopat eivät ole erillisiä, joten esimerkiksi viidellä nopalla tuloksia 1-1-3-5-6 ja 1-6-5-1-3 pidettäisiin samana heittona. Kahdella nopalla on triviaalia määrittää, että vastaus on 21, mutta en löydä eleganttia, yleistettyä ratkaisua.

Don alkaen New York

Vastaus voidaan ilmaista muodossa combin(n+5,n) = (n+5)!/(120×n!). Tässä on vastaus 1–20 nopalle.

Epätyypilliset noppayhdistelmät

Nopat Yhdistelmät
1 6
2 21
3 56
4 126
5 252
6 462
7 792
8 1287
9 2002
10 3003
11 4368
12 6188
13 8568
14 11628
15 15504
16 20349
17 26334
18 33649
19 42504
20 53130
21 65780
22 80730
23 98280

Kiitokset Alan Tuckerille, teoksen Applied Combinatorics kirjoittajalle.

Voitko laskea, mikä on todennäköisyys sille, että nopanheitossa tulee kaksi numeroa peräkkäin? Eli mikä on todennäköisyys sille, että kaksi nelosta, kaksi kuutosta tai kaksi seiskaa tulee peräkkäin? Ymmärrän, ettei menneisyys voi ennustaa tulevaisuutta, mutta onko olemassa tapaa laskea, että 7/36 x 7/36 tapahtuu peräkkäin? Toivottavasti tämä on järkevää.

James alkaen Birmingham

Totta kai. Se olisi Pr(2) ² + Pr(3) ² + ... + Pr(12) ² = (1/36) ² + (2/36) ² + (3/36) ² + (4/36) ² + (5/36) ² + (6/36) ² + (5/36) ² + (4/36) ² + (3/36) ² + (2/36) ² + (1/36) ² = 11,27 %.
Kuinka monta kertaa voin odottaa näkeväni seuraavat 180 peräkkäisen nopanheiton aikana?

Kaksi seitsemää peräkkäin?
Kolme seitsemää peräkkäin?
Neljä seitsemää peräkkäin?

Kiitos ajastasi :-).

Melanie D. alkaen Elizabeth City, NC

En keksi mitään hyödyllistä syytä tietää tätä tietoa, mutta minulta kysytään tällaisia asioita usein, joten yritän miellyttää sinua.

Ensimmäisestä heitosta alkaen tai viimeiseen päättyen tietyn seiskien sarjan saaminen on hieman helpompaa, koska sarja on rajoitettu yhdeltä puolelta. Tarkemmin sanottuna todennäköisyys saada s seiskan sarja ensimmäisestä heitosta alkaen tai viimeiseen päättyen on (1/6) s × (5/6). 5/6-termi johtuu siitä, että sarjan avoimeen päähän on saatava muu kuin 7.

Todennäköisyys sille, että s seiskan sarja alkaa missä tahansa pisteessä sarjan keskellä, on (1/6) s × (5/6) 2 . Neliöimme 5/6-termin, koska pelaajan on saatava muu kuin 7 sarjan molempiin päihin.

Jos heittoja on r, sisäpuoliselle sarjalle on kaksi sijaa ja n seiskan sarjalle rn-1 sijaa. Laittamalla nämä yhtälöt taulukkoon saadaan odotettu seiskien sarjamäärä välillä 1-10. "Sisäpuolinen"-sarake on 2*(5/6)*(1/6) r ja "ulkopuolinen"-sarake on (179-r)*(5/6) 2 *(1/6) r , missä r on seiskojen lukumäärä sarjassa. Joten voimme odottaa 3,46 kahden seiskan sarjaa, 0,57 kolmen seiskan sarjaa ja 0,10 neljän seiskan sarjaa.

Odotetut seiskakierrokset 180 heitossa

Juokse Sisällä Ulkopuolella Kokonais
1 0,277778 20.601852 20.87963
2 0,046296 3.414352 3.460648
3 0,007716 0,565844 0,57356
4 0,001286 0,093771 0,095057
5 0.000214 0,015539 0,015754
6 0.000036 0,002575 0,002611
7 0.000006 0,000427 0,000433
8 0.000001 0,000071 0,000072
9 0 0.000012 0.000012
10 0 0,000002 0,000002
Kahta noppaa heitetään, kunnes joko luku on 12 tai kaksi peräkkäistä lukua 7. Mikä on todennäköisyys, että 12 heitetään ensin?

anonyymi

Vastaus ja ratkaisu löytyvät kumppanisivustoltani mathproblems.info , tehtävästä 201.
Olen pöytäpelaaja ja keskustelin ystävieni kanssa ei-kuutiollisista platonisista kiinteistä nopista (jos olet tarpeeksi iso nörtti, se tarkoittaa d4, d8, d12 ja d20). He väittivät, että ne olisivat ainoat, jotka olisivat demonstratiivisesti reiluja. Minä väitin, että niiden valmistaminen reiluiksi olisi aivan liian vaikeaa. Lisäksi ainoat pelit olisivat craps-muunnelmat, jotka olisivat liian kömpelöitä lisätulosten määrän vuoksi. Onko millään kasinolla koskaan ollut peliä, jossa olisi käytetty epäperinteisiä kuusisivuisia noppaa?

Bayani alkaen Carnagie, PA


Tämä on Lisa Furman, malli M-kasinoarvostelustani . Kun yritin tehdä häneen vaikutuksen sanomalla, että vasemmalla oleva ilmapallokuvio on katkaistu ikosaedri , hän vain hymyili ja pyöritteli silmiään.

Älä uskalla kyseenalaistaa matematiikan nörttitaitojani! Kun olin lukion toisen vuoden opiskelija, rakensin paitsi kaikki platoniset kappaleet julistepahvilla ja sähköteipillä, myös kaikki Arkhimedeen kappaleet .

Jos rajoitut säännöllisiin monikulmioihin ja haluat, että jokaisella pinnalla on sama todennäköisyys, olet rajoittunut platonisiin kappaleisiin. Jos kuitenkin voit poistaa säännöllisen monikulmion vaatimuksen, voit lisätä myös 13 Katalonin kappaletta .

Vastauksena toiseen kysymykseesi, en ole koskaan nähnyt kasinolla peliä, jossa käytettäisiin muita noppaa kuin kuutioita. Noin kymmenen vuotta sitten näin Atlantic Cityssä pelimessuilla pelin, jossa mielestäni käytettiin rombista triakontaedriä , yhtä katalaanilaisista kappaleista, mutta en usko, että se koskaan päätyi kasinon lattialle. Näen vuodesta toiseen Global Gaming Expossa pelin, jossa käytetään hyrrää (kuten dreideliä), mutta valitettavasti en ole koskaan nähnyt sellaistakaan kasinolla.

Jos heitän kolme kuusisivuista noppaa, mitkä ovat todennäköisyydet saada suora ja myös mitkä ovat todennäköisyydet saada kolmoset?

Mark alkaen Fargo, ND

Kolmen noppaa voi heittää 6 * 3 = 216 tavalla. Kuusi näistä yhdistelmistä johtaa kolmoseen (1-1-1 - 6-6-6). Joten kolmosen todennäköisyys on 6/216 = 1/36. Suoralle on neljä mahdollista väliä (1-2-3 - 4-5-6). Kolme noppaa voi myös järjestää suoraksi 3! = 6 tavalla. Suoria on siis 4 * 6 = 24. Suoran todennäköisyys on siis 24/216 = 1/9.
Mikä on neljän kuusisivuisen noppaa heitettäessä saatujen tulosten keskiarvo pienimmän tuloksen (eli 4d6-L) vähentämisen jälkeen? Mikä on tämän heiton keskihajonta?

Aaron alkaen New York

Seuraava taulukko näyttää kaikkien mahdollisten yhdistelmien määrän 3:sta 18:aan.

Yhdistelmät 4d6-L:ssä

Tulokset Yhdistelmät
3 1
4 4
5 10
6 21
7 38
8 62
9 91
10 122
11 148
12 167
13 172
14 160
15 131
16 94
17 54
18 21
Kokonais 1296

Keskiarvo on 12,2446 ja keskihajonta on 2,8468.

Kysymykseni perustuu nopanheiton todennäköisyyksiin. Tiedän, että on kuusi tapaa saada luku 7 ja yksi tapa saada luku 12, mutta mitkä ovat mahdollisuudet saada kuusi lukua seiskoja ennen yhtä lukua 12? Ovatko ne parillisia, ja jos eivät, kuinka monta kaksitoista pitäisi lisätä yhtälöön, jotta se olisi parillinen väite?

nick

Todennäköisyys sille, että heitetään luku 7, on 1/6 ja todennäköisyys sille, että heitetään luku 12, on 1/36. Todennäköisyys sille, että heitetään luku 7 tai 12, on (1/6)/((1/6)+(1/36)) = 6/7. Joten todennäköisyys sille, että ensimmäiset kuusi kertaa, kun heitetään luku 6 tai 12, se on joka kerta 6, on (6/7) 6 = 39,66 %.

Jos muotoilet kysymyksen uudelleen ja kysyt todennäköisyyttä sille, että ennen lukua 12 tulee viisi kuutosia, vastaus on (6/7) 5 = 46,27 %. Neljällä heitolla se on (6/7) 4 = 53,98 %. Joten ennen lukua 12 ei ole olemassa sellaista määrää seiskoja, joka olisi täsmälleen 50/50. Jos etsit hyvää huonoa vetoa, ehdotan, että voit joko heittää neljä seiskaa ennen lukua 12 tai 12:n ennen viittä seiskaa.

Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.

Onko olemassa helppoa tapaa laskea todennäköisyys heittää yhteensä t d:llä kuusisivuisella nopalla?

Anon E. Mouse

Tässä on kätevä kikka Robert Goodhandin Somersetista, Isosta-Britanniasta, luvalla. Laita ensin riville kuusi ykköstä ja niiden molemmille puolille viisi nollaa seuraavasti:

Yhden nopan todennäköisyydet

Noppien kokonaismäärä 1 2 3 4 5 6
Yksi kuolee 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0

Tämä edustaa yhdistelmien lukumäärää, kun yhdellä nopalla heitetään luku 1–6. Tiedän, aika itsestään selvää. Pysy kuitenkin mukana. Kahdelle nopalle lisää uusi rivi loppuun ja laske jokaiselle ruudulle yläpuolella olevan rivin ja sen vasemmalla puolella olevien viiden ruudun summa. Lisää sitten oikealle viisi vale-nollaa, jos haluat jatkaa. Tämä edustaa yhdistelmien lukumäärää, kun heitetään yhteensä lukuja 2–12.

Kahden nopan todennäköisyydet

Noppien kokonaismäärä 2 3 4 5 6 7 8 9 10 11 12
Yksi kuolee 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
Kaksi noppaa 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0

Kolmen nopan kohdalla toista tämä. Tämä edustaa yhdistelmien määrää 3:sta 18:aan.

Kolmen nopan todennäköisyydet Laajenna

Noppien kokonaismäärä 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Yksi kuolee 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Kaksi noppaa 0 0 0 0 0 1 2 3 4 5 6 5 4 3 2 1 0 0 0 0 0 0 0 0 0 0
Kolme noppaa 0 0 0 0 0 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1 0 0 0 0 0

Saadaksesi minkä tahansa annetun kokonaissumman todennäköisyyden, jaa kyseisen kokonaissumman yhdistelmien lukumäärä yhdistelmien kokonaismäärällä. Kolmen nopan tapauksessa summa on 216, joka on myös helposti löydettävissä muodossa 6 3. Esimerkiksi todennäköisyys saada yhteensä 13 kolmella nopalla on 21/216 = 9,72 %.

Joten d-noppien kohdalla sinun täytyy työskennellä 1:stä d-1 noppaan. Tämä on erittäin helppoa millä tahansa taulukkolaskentaohjelmalla.

Kuinka monta kahden nopan heittoa tarvitaan, jotta ainakin yhden tuloksen 12 todennäköisyys olisi 50/50?

Maff

Tämä on klassinen ongelma todennäköisyyslaskennan historiassa. Monet ihmiset virheellisesti luulevat vastauksen olevan 18, koska luvun 12 todennäköisyys on 1/36 ja 18 × (1/36) = 50 %. Tämän logiikan mukaan luvun 12 todennäköisyys 36 heitolla olisi kuitenkin 100 %, mikä se ei selvästikään ole. Tässä on oikea ratkaisu. Olkoon r heittojen lukumäärä. Todennäköisyys sille, että heitto ei ole 12, on 35/36. Todennäköisyys, että r heitolla on 0 12:ta, on (35/36) r . Joten meidän on ratkaistava r seuraavassa yhtälössä:

(35/36) r = 0,5
log(35/36) r = log(0,5)
r × log(35/36) = log(0,5)
r = log(0,5)/log(35/36)
r = 24,6051

Joten pyöreää vastausta ei ole. Todennäköisyys saada 12 24 heitolla on 1-(35/36) 24 = 49,14 %. Todennäköisyys saada 12 25 heitolla on 1-(35/36) 25 = 50,55 %.

Jos haluat lyödä vetoa tästä, sanotaan, että saat 25 heitolla tulokseksi 12 tai joku muu ei saa sitä 24 heitolla. Kummassakin tapauksessa sinulla on etulyöntiasema tasatilanteessa.

Mikä on Noppasodan onnistumisen todennäköisyys millä tahansa hyökkäävien ja puolustavien noppien määrällä? Millä hyökkääjänä on suurin odotettu voitto?

odiousgambit

Niille, jotka eivät ole perehtyneet peliin, sekä hyökkääjä että puolustaja heittävät 1–8 noppaa sen mukaan, kuinka monta armeijaa heillä kummallakin on taistelun kyseisessä vaiheessa. Suurempi luku voittaa. Tasapeli menee puolustajalle. Jos hyökkääjä häviää, hän säilyttää edelleen yhden armeijan alueella, josta hän aloitti hyökkäyksen. Tästä syystä hänellä on oltava vähintään kaksi armeijaa hyökätäkseen, joten jos hän voittaa, toinen voi asua valloitetulla alueella ja toinen jäädä.

Seuraava taulukko näyttää hyökkääjän voiton todennäköisyyden kaikkien 64 nopanheittoyhdistelmän perusteella.

Hyökkääjän voiton todennäköisyys

Hyökkääjä Puolustaja
1. armeija 2 armeijaa 3 armeijaa 4 armeijaa 5 armeijaa 6 armeijaa 7 armeijaa 8 armeijaa
2 0,837963 0,443673 0.152006 0,035880 0,006105 0,000766 0,000071 0.000005
3 0,972994 0,778549 0,453575 0.191701 0,060713 0,014879 0,002890 0,000452
4 0,997299 0,939236 0,742831 0,459528 0.220442 0,083423 0,025450 0,006379
5 0.999850 0.987940 0,909347 0,718078 0,463654 0.242449 0.103626 0,036742
6 0,999996 0.998217 0,975300 0,883953 0.699616 0,466731 0,259984 0.121507
7 1.000000 0.999801 0,994663 0,961536 0,862377 0,685165 0,469139 0,274376
8 1.000000 0,999983 0,999069 0.989534 0,947731 0,843874 0,673456 0,471091

Seuraava taulukko näyttää hyökkääjän odotetun voiton, joka on määritelty muodossa pr(hyökkääjän voitto)*(puolustajan noppa)+pr(puolustajan voitto)*(hyökkääjän noppa -1). Se osoittaa, että suurin odotettu voitto on hyökätä luvulla 8 vastustajaa vastaan, jolla on luvulla 5.

Hyökkääjän voiton nettotulos

Hyökkääjä Puolustaja
1. armeija 2 armeijaa 3 armeijaa 4 armeijaa 5 armeijaa 6 armeijaa 7 armeijaa 8 armeijaa
2 0,675926 0.331019 -0,391976 -0,820600 -0,963370 -0,994638 -0,999432 -0,999955
3 0,918982 1.114196 0,267875 -0,849794 -1,575009 -1,880968 -1,973990 -1,995480
4 0,989196 1.696180 1,456986 0,216696 -1,236464 -2,249193 -2,745500 -2,929831
5 0,999250 1.927640 2.365429 1.744624 0,172886 -1,575510 -2,860114 -3,559096
6 0,999976 1.987519 2.802400 2.955577 1.996160 0,134041 -1,880192 -3,420409
7 1.000000 1.998408 2.951967 3.615360 3.486147 2.221980 0,098807 -2,158736
8 1.000000 1.999847 2.990690 3.884874 4.372772 3.970362 2.428384 0,066365

Mikä on todennäköisyys muodostaa Yahtzee jopa n nopanheitolla?

anonyymi

Muiden lukijoiden tiedoksi, Yahtzee on viisi samanlaista peliä, jossa on viisi noppa. Yahtzee-pelissä pelaaja voi pitää mitä tahansa noppia ja heittää loput uudelleen. Hän voi tehdä tämän enintään kolme kertaa.

Pelaaja voi halutessaan heittää aiemmin hallussaan pitämänsä nopan uudelleen. Esimerkiksi jos pelaajan ensimmäinen heitto on 3-3-4-5-6 ja hänellä on kolmoset ja toisen heiton jälkeen on 3-3-5-5-5, hän voi pitää vitoset ja heittää kolmoset uudelleen kolmannella heitollaan.

Seuraava taulukko näyttää samannäköisten noppien enimmäismäärän 1–20 heitolla. Taulukosta käy ilmi, että Yatzy-voiton todennäköisyys kolmen heiton aikana on noin 4,6 %.

Yahtzee-todennäköisyydet

Rullat Saman puolen noppien enimmäismäärä
Yksi Kaksi Kolme Neljä Viisi
1 0,092593 0.694444 0.192901 0,019290 0,000772
2 0,008573 0,450103 0,409022 0.119670 0,012631
3 0,000794 0.256011 0,452402 0,244765 0,046029
4 0.000074 0.142780 0.409140 0,347432 0.100575
5 0.000007 0,079373 0.337020 0,413093 0,170507
6 0.000001 0,044101 0,263441 0,443373 0,249085
7 0.000000 0,024501 0.199279 0,445718 0,330502
8 0.000000 0,013612 0,147462 0.428488 0,410438
9 0.000000 0,007562 0.107446 0.398981 0.486011
10 0.000000 0,004201 0,077416 0,362855 0,555528
11 0.000000 0,002334 0,055317 0,324175 0,618174
12 0.000000 0,001297 0,039279 0,285674 0,673750
13 0.000000 0,000720 0,027757 0,249063 0,722460
14 0.000000 0.000400 0,019543 0,215313 0,764744
15 0.000000 0,000222 0,013720 0.184883 0.801175
16 0.000000 0.000124 0,009610 0,157896 0,832371
17 0.000000 0.000069 0,006719 0,134258 0.858954
18 0.000000 0.000038 0,004692 0.113753 0.881517
19 0.000000 0.000021 0,003272 0,096100 0,900607
20 0.000000 0.000012 0,002280 0,080994 0,916714


Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Mietin, kumpi tulee useammin esiin nopanheitossa – pariton vai parillinen summa?

relaxmax

Vastaus on 50/50. Tämä pätee mihin tahansa noppien määrään, ei vain kahteen.

Hieman aiheesta poiketen, olen aina ajatellut, että pariton/parillinen panostussarja olisi hyvä tapa korvata pelätyt isot 6/8-panokset crapsissa. Antaakseni talolle etua, tässä ovat ehdotukseni voittotaulukoista ja analyysistä.

Pariton veto

Tapahtuma Maksaa Yhdistelmät Todennäköisyys Palata
3 tai 11 1.5 4 0.111111 0,166667
5 tai 9 1 8 0.222222 0.222222
7 0,5 6 0,166667 0,083333
Jopa -1 18 0,500000 -0,500000
Kokonais 36 1.000000 -0,027778

Tasainen veto

Tapahtuma Maksaa Yhdistelmät Todennäköisyys Palata
2 tai 12 3 2 0,055556 0,166667
4 tai 10 1 6 0,166667 0,166667
6 tai 8 0,5 10 0,277778 0.138889
Pariton -1 18 0,500000 -0,500000
Kokonais 36 1.000000 -0,027778


Huomaathan, että minulla on kaikki oikeudet tähän julkaisuun.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Hot Roll -bonuspelissä pelaaja voittaa seuraavan määrän kolikoita kahden nopan yhteissumman mukaan:

  • 2 tai 12: 1000
  • 3 tai 11: 600
  • 4 tai 10: 400
  • 5 tai 9: 300
  • 6 tai 8: 200


Hän heittää, kunnes saa yhteensä seitsemän, mikä lopettaa bonuksen. Jos hän heittää ensimmäisellä heitolla seitsemän, hän saa lohdutuspalkinnon 700 kolikkoa. Mikä on keskimääräinen voitettujen kolikoiden määrä bonusta kohden?

anonyymi

Keskimääräinen heittojen määrä on käänteisluku bonuspelin päättymistapahtumaan verrattuna, jonka todennäköisyys on 1/6, joten pelaaja heittää keskimäärin kuusi kertaa. Viimeinen heitto on kuitenkin seitsemän, joten voittoheittoja on keskimäärin viisi bonuspeliä kohden.

Seuraavaksi, tässä on kunkin kokonaissumman todennäköisyys, olettaen ettei seitsemää ole:

  • 2 tai 12: 1/30
  • 3 vai 11: 30.2.
  • 4 vai 10: 3/30
  • 5 tai 9: 4/30
  • 6 tai 8: 30.5.


Keskimääräinen voitto heittoa kohden, olettaen, ettei heittoja ole seitsemää, on siis 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373,33.

Lohdutuspalkinnon arvo on (1/6) * 700 = 116,67.

Näin ollen keskimääräinen bonusvoitto on 116,67 + 5 × 373,33 = 1983,33.

Mikä olisi vastaus Kysy velholta -palstan 179 noppatehtävään, jos pelaajat heittäisivät vuorotellen noppaa ja vain noppaa heittänyt pelaaja voisi edetä heiton perusteella?

anonyymi

Tässä oli alkuperäinen kysymys sarakkeessa #179: Jos kahta noppaa heitetään yhä uudelleen ja uudelleen, kunnes jompikumpi seuraavista tapahtumista tapahtuu, kumpi todennäköisemmin tapahtuu ensin?

  • Yhteensä heitetään kuusi ja kahdeksan, kummassakin järjestyksessä, ja kaksoiskappaleet sallitaan.
  • Yhteensä seitsemän heitetään kahdesti.

Juttusi on siinä, että sama heitto ei voi auttaa molempia pelaajia. Sen sijaan he heittävät vuorotellen ja vain se, joka heittää, voi käyttää heittonsa.

Vastaus riippuu siitä, kumpi heittää ensin. Jos pelaaja, joka tarvitsee kuutonen ja kahdeksikon, heittää ensin, hänen voittotodennäköisyytensä on 57,487294 %. Jos pelaaja, joka tarvitsee kaksi seiskaa, heittää ensin, todennäköisyys sille, että pelaaja, joka tarvitsee kuutonen ja kahdeksikon, voittaa, on 52,671614 %. Ratkaisin sen käyttämällä yksinkertaista Markov-ketjuprosessia.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Oletetaan, että sinulla on 12 kuusisivuista noppaa. Heität ne ja voit laittaa sivuun haluamasi nopat. Sitten heität muut nopat uudelleen. Mikä on todennäköisyys saada molemmilla heitoilla 12 samaa numeroa?

anonyymi

Ensimmäisellä heitolla on 58 erilaista sarjaa. Tunnistan jokaisen sarjan numerolla, sitten toisella sijalla olevan nopan lukumäärällä ja niin edelleen. Esimerkiksi heitto, jonka arvo on 3, 3, 3, 3, 6, 6, 6, 5, 5, 2, merkitään muodossa 4-3-2-1. Seuraava taulukko näyttää kunkin sarjan yhdistelmien lukumäärän, sen heittämisen todennäköisyyden, todennäköisyyden saada 12 samaa tyyppiä toisella heitolla ja näiden kahden tulon. Toisen heiton todennäköisyyden laskemiseksi oletan, että pelaajalla on nopat, joiden yhteissumma ensimmäisellä heitolla on suurin. Oikeassa alakulmassa oleva solu näyttää kokonaistodennäköisyydeksi 0,0000037953, joka on yhtä kuin 1/263 486.

12 nopan kysymys

Sarja Yhdistelmät Todennäköisyys
Sarja		 Ehdollinen
Todennäköisyys		 Kokonais
Todennäköisyys
12-0-0-0-0-0-0 6 0.0000000028 1.0000000000 0.0000000028
11-1-0-0-0-0 360 0.0000001654 0.1666666667 0.0000000276
10-2-0-0-0-0 1 980 0.0000009096 0.0277777778 0.0000000253
10-1-1-0-0-0 7 920 0.0000036384 0.0277777778 0.0000001011
9-3-0-0-0-0 6 600 0.0000030320 0.0046296296 0.0000000140
9-2-1-0-0-0 79 200 0.0000363840 0.0046296296 0.0000001684
9-1-1-1-1-0-0 79 200 0.0000363840 0.0046296296 0.0000001684
8-4-0-0-0-0 14 850 0.0000068220 0.0007716049 0.0000000053
8-3-1-0-0-0 237 600 0.0001091519 0.0007716049 0.0000000842
8-2-2-0-0-0 178 200 0.0000818639 0.0007716049 0.0000000632
8-2-1-1-0-0 1 069 200 0.0004911837 0.0007716049 0.0000003790
8-1-1-1-1-1-0 356 400 0.0001637279 0.0007716049 0.0000001263
7-5-0-0-0-0 23 760 0.0000109152 0.0001286008 0.0000000014
7-4-1-0-0-0 475 200 0.0002183039 0.0001286008 0.0000000281
7-3-2-0-0-0 950 400 0.0004366077 0.0001286008 0.0000000561
7-3-1-1-0-0 2 851 200 0.0013098232 0.0001286008 0.0000001684
7-2-2-1-0-0 4 276 800 0.0019647348 0.0001286008 0.0000002527
7-2-1-1-1-1-0 5 702 400 0.0026196464 0.0001286008 0.0000003369
7-1-1-1-1-1-1 570 240 0.0002619646 0.0001286008 0.0000000337
6-6-0-0-0-0 13 860 0.0000063672 0.0000214335 0.0000000001
6-5-1-0-0-0 665 280 0.0003056254 0.0000214335 0.0000000066
6-4-2-0-0-0 1 663 200 0.0007640635 0.0000214335 0.0000000164
6-4-1-1-0-0 4 989 600 0.0022921906 0.0000214335 0.0000000491
6-3-3-0-0-0 1 108 800 0.0005093757 0.0000214335 0.0000000109
6-3-2-1-0-0 19 958 400 0.0091687624 0.0000214335 0.0000001965
6-3-1-1-1-0 13 305 600 0.0061125083 0.0000214335 0.0000001310
6-2-2-2-0-0 4 989 600 0.0022921906 0.0000214335 0.0000000491
6-2-2-1-1-0 29 937 600 0.0137531436 0.0000214335 0.0000002948
6-2-1-1-1-1-1 9 979 200 0.0045843812 0.0000214335 0.0000000983
5-5-2-0-0-0 997 920 0.0004584381 0.0000035722 0.0000000016
5-5-1-1-0-0 2 993 760 0.0013753144 0.0000035722 0.0000000049
5-4-3-0-0-0 3 326 400 0.0015281271 0.0000035722 0.0000000055
5-4-2-1-0-0 29 937 600 0.0137531436 0.0000035722 0.0000000491
5-4-1-1-1-1-0 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-3-3-1-0-0 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-3-2-2-0-0 29 937 600 0.0137531436 0.0000035722 0.0000000491
5-3-2-1-1-0 119 750 400 0.0550125743 0.0000035722 0.0000001965
5-3-1-1-1-1-1 19 958 400 0.0091687624 0.0000035722 0.0000000328
5-2-2-2-1- 59 875 200 0,0275062872 0.0000035722 0.0000000983
5-2-2-1-1-1 59 875 200 0,0275062872 0.0000035722 0.0000000983
4-4-4-0-0-0 693 000 0.0003183598 0.0000005954 0.0000000002
4-4-3-1-0-0 24 948 000 0.0114609530 0.0000005954 0.0000000068
4-4-2-2-0-0 18 711 000 0.0085957147 0.0000005954 0.0000000051
4-4-2-1-1-0 74 844 000 0,0343828589 0.0000005954 0.0000000205
4-4-1-1-1-1-1 12 474 000 0.0057304765 0.0000005954 0.0000000034
4-3-3-2-0-0 49 896 000 0.0229219060 0.0000005954 0.0000000136
4-3-3-1-1-0 99 792 000 0.0458438119 0.0000005954 0.0000000273
4-3-2-2-1-0 299 376 000 0.1375314358 0.0000005954 0.0000000819
4-3-2-1-1-1 199 584 000 0.0916876238 0.0000005954 0.0000000546
4-2-2-2-2-2-0 37 422 000 0.0171914295 0.0000005954 0.0000000102
4-2-2-2-1-1 149 688 000 0,0687657179 0.0000005954 0.0000000409
3-3-3-3-0-0 5 544 000 0.0025468784 0.0000000992 0.0000000003
3-3-3-2-1-0 133 056 000 0.0611250826 0.0000000992 0.0000000061
3-3-3-1-1-1 44 352 000 0.0203750275 0.0000000992 0.0000000020
3-3-2-2-2-0 99 792 000 0.0458438119 0.0000000992 0.0000000045
3-3-2-2-1-1 299 376 000 0.1375314358 0.0000000992 0.0000000136
3-2-2-2-2-2-1 149 688 000 0,0687657179 0.0000000992 0.0000000068
2-2-2-2-2-2-2 7 484 400 0.0034382859 0.0000000165 0.0000000001
Kokonais 2 176 782 336 1.0000000000 0.0000037953
Kuinka monta kertaa keskimäärin reilun kokoista nopanheittoa tarvitaan, jotta jokainen sivu saadaan heitettyä vähintään kaksi kertaa?

Ace2

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

Vastaus on 1 172 906 043 / 48 600 000 = noin 24,13387 pikseliä

Tässä on ratkaisuni . (PDF)

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Oletetaan, että heitetään reilua kuusisivuista noppaa, kunnes tulokseen tulee 1, 2, 3 tai 6. Jos 1, 2 tai 3 on ensimmäinen näistä pelin loppunumeroista, et voita mitään. Jos 6 on ensimmäinen näistä pelin loppunumeroista, voitat 1 dollarin jokaisesta nopanheitosta. Mikä on pelin keskimääräinen voitto?

Klopp

Napsauta alla olevaa painiketta nähdäksesi muutamia äärettömien sarjojen kaavoja, joista voi olla sinulle hyötyä.

Vihje 1: Laske summa, kun i = 0 - ∞ n:stä, jolloin i = 1 / (1 - n)

Vihje 2: Laske summa, kun i = 0 - ∞, i × n i = n / (1-n) ²

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

Vastaus on 3/4.

Napsauta alla olevaa painiketta nähdäksesi ratkaisun.

Oletetaan, että heitetään reilua kuusisivuista noppaa, kunnes tulokseen tulee 1, 2, 3 tai 6. Jos 1, 2 tai 3 on ensimmäinen näistä pelin loppunumeroista, et voita mitään. Jos 6 on ensimmäinen näistä pelin loppunumeroista, voitat 1 dollarin jokaisesta nopanheitosta. Mikä on pelin keskimääräinen voitto?

Vihje 1: Laske summa, kun i = 0 - ∞ n:stä, jolloin i = 1 / (1 - n)

Vihje 2: Laske summa, kun i = 0 - ∞, i × n i = n / (1-n) ²

Odotusarvoinen voitto voidaan ilmaista summana (1 + i) * (1/3) i * (1/6), kun i = 0 - ∞. =

(1/6) * summa, kun i = 0 - ∞ (1/3) i:stä + (1/6) * summa, kun i = 0 - ∞ (i * (1/3) i:stä ).

Arvioidaan näitä yksi kerrallaan.

summa, kun i = 0 - ∞ (1/3) i =

1 / (1 - (1/3)) =

1 / (2/3) =

3/2

Summa, kun i = 0 - ∞ joukosta (i * (1/3) i ) =

(1/3) / (1 - (1/3)) 2 =

(1/3) / (4/9) =

(1/3) * (9/4) =

3/4

Kaiken kaikkiaan vastaus on

(1/6) * (3/2) + (1/6) * (3/4) =

(1/4) + (1/8) =

3/8

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kuinka monta kertaa reilua noppaheittoa odotetaan tapahtuvan niin, että jokainen sivu on vähintään kaksi kertaa oikeassa paikassa?

Ace2

Vastaus on 390968681 / 16200000 = noin 24.13386919753086

Vaikka tämä voitaisiin ratkaista pitkällä ja työläällä Markov-ketjulla, pidän parempana integraaliratkaisua. Selitän, kuinka tätä menetelmää käytetään Fire Bet- ja Bonus Craps -sivuillani.

Kuvittele, että merkittävien tapahtumien yksi kerrallaan määrittämisen sijaan nopanheitto voi tarkoittaa yksittäisiä hetkiä. Oletetaan, että tapahtumien välinen aika ei kata muistia ja että tapahtumien välinen keskimääräinen aika on yksi aikayksikkö. Toisin sanoen tapahtumien välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 1. Tällä ei ole merkitystä vedon ratkaisemisen kannalta, koska tapahtumat tapahtuvat edelleen yksi kerrallaan.

Poissonin jakauman mukaan todennäköisyys sille, että mitä tahansa nopan sivua on heitetty nolla kertaa x aikayksikössä, on exp(-x/6)*(x/6) 0 /0! = exp(-x/6). Poissonin jakauman mukaan todennäköisyys sille, että mitä tahansa sivua on heitetty tasan kerran, on exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6). Näin ollen todennäköisyys sille, että mitä tahansa sivua on heitetty kaksi tai useampia kertoja x aikayksikössä, on 1 - exp(-x/6)*(1 + (x/6)). Todennäköisyys sille, että kaikki kuusi sivua on heitetty vähintään kaksi kertaa, on (1 - exp(-x/6)*(1 + (x/6))) 6. Todennäköisyys sille, että ainakin yhtä sivua ei ole heitetty vähintään kaksi kertaa, on yhtä suuri kuin:

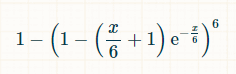
rullaa joka puolelta kahdesti

Meidän on integroitava se koko ajan, jotta löydämme, kuinka paljon aikaa keskimäärin kuluu, jos haluttua tavoitetta ei ole saavutettu.

Onneksi voimme tässä vaiheessa käyttää integraalilaskuria . Linkitettyä laskuria varten kirjoita 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 tekstikenttään "Laske :n integraali" ja aseta mukautettu-kohdasta integroinnin rajaksi 0:sta ∞:aan.

Vastaus on 390968681 / 16200000 = noin 24,13386919753086

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Aloitat reilun kokoisella kuusisivuisella nopalla ja heität sitä kuusi kertaa ja kirjaat jokaisen heiton tulokset muistiin. Sitten kirjoitat nämä numerot toisen, nimeämättömän reilun kokoisen nopan kuudelle sivulle. Esimerkiksi, jos kuusi heittoasi olivat 3, 5, 3, 6, 1 ja 2, toisessa nopassasi ei olisi numeroa 4; sen sijaan siinä olisi kaksi numeroa 3.

Seuraavaksi heität tätä toista noppaa kuusi kertaa. Ota nämä kuusi numeroa ja kirjoitat ne seuraavan reilusti nopan sivuille ja jatkat tätä prosessia, jossa luot uuden nopan edellisestä.

Lopulta sinulla on noppa, jonka kaikilla kuudella sivulla on sama numero. Mikä on keskimääräinen siirtymien määrä nopasta toiseen (tai heittojen kokonaismäärä jaettuna kuudella), jotta saavutetaan tämä tila?

rsactuary

Noin 9.65599148388557

Merkitään alkuperäinen noppa kirjaimilla numeroiden sijaan sekaannusten välttämiseksi. Merkitään jokainen mahdollinen nopan tila kirjaimilla. Esimerkiksi AAABBBC tarkoittaisi kolmea yhdestä kirjaimesta, kahta toisesta ja yhtä kolmannesta. Alkutila olisi luonnollisesti ABCDEF.

Olkoon E(ABCDEF) odotettu heittojen lukumäärä tilasta ABCDEF.

P 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656

Seuraava siirtymämatriisi näyttää, kuinka monella tavalla kustakin alkutilasta (vasen sarake) uuteen tilaan voi siirtyä, perustuen tilasta toiseen siirtymisen yhdistelmien määrään. Tämän rakentaminen vei muuten muutaman tunnin.

Siirtymämatriisi A

Osavaltio
Ennen		 AAAAAAA AAAAAB AAAABB AAAABBB AAAABC AAAABC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB 15 626 18 780 9 750 2 500 - - - - - - -
AAAABB 4 160 13 056 19 200 10 240 - - - - - - -
AAAABBB 1 458 8 748 21 870 14 580 - - - - - - -
AAAABC 4 098 12 348 8 190 2 580 7 920 10 080 1 440 - - - -
AAAABC 794 5 172 8 670 5 020 6 480 17 280 3 240 - - - -
AABBCC 192 2 304 5 760 3 840 5 760 23 040 5 760 - - - -
AAABCD 732 4 464 4 140 1 680 7 920 14 400 2 520 4 320 6 480 - -
AABBCD 130 1 596 3 150 1 940 5 280 16 800 3 600 4 800 9 360 - -
AABCDE 68 888 1 380 760 3 960 11 520 2 520 7 200 14 040 4 320 -
ABCDEF 6 180 450 300 1 800 7 200 1 800 7 200 16 200 10 800 720

En aio mennä pitkälle luennolle matriisialgebrasta, paitsi että sanotaan vaikka, että matriisi B on seuraava:

Matriisi B

Osavaltio
Ennen		 AAAAAB AAAABB AAAABBB AAAABC AAAABC AABBCC AAABCD AABBCD AABCDE ABCDEF
AAAAAB -27876 9750 2500 0 0 0 0 0 0 -46656
AAAABB 13056 -27456 10240 0 0 0 0 0 0 -46656
AAAABBB 8748 21870 -32076 0 0 0 0 0 0 -46656
AAAABC 12348 8190 2580 -38736 10080 1440 0 0 0 -46656
AAAABC 5172 8670 5020 6480 -29376 3240 0 0 0 -46656
AABBCC 2304 5760 3840 5760 23040 -40896 0 0 0 -46656
AAABCD 4464 4140 1680 7920 14400 2520 -42336 6480 0 -46656
AABBCD 1596 3150 1940 5280 16800 3600 4800 -37296 0 -46656
AABCDE 888 1380 760 3960 11520 2520 7200 14040 -42336 -46656
ABCDEF 180 450 300 1800 7200 1800 7200 16200 10800 -46656

Vastaus on matriisin B determinantin ja matriisin A determinantin suhde:

Määritä(A) = 1 461 067 501 120 670 000 000 000 000 000 000 000 000 000 000 000

Määritä(B) = 14 108 055 348 203 100 000 000 000 000 000 000 000 000 000 000

Määritä(B) / Määritä(A) = noin 9,65599148388557

Jos heität yhtä noppaa 20 kertaa, mikä on todennäköisyys, että osut kaikkiin kuuteen sivuun ainakin kerran?

Ace2

Vastaus on noin 0.847987541

Vastaus voidaan approksimoida seuraavasti: 1 - (prob(ei 1:tä) + prob(ei 2:ta) + ... + prob(ei 6:tta)) = 1 - 6*(5/6)^20 = n. 0,84349568.

Tämä kuitenkin vähentäisi kaksinkertaisesti tilanteet, joissa kahta eri sivua ei koskaan heitetty. Kuudesta sivusta voi valita kaksi combin(6,2)=15 tavalla. Todennäköisyys sille, että mitkä tahansa kaksi sivua eivät koskaan tule heitetyksi, on (4/6)^20. Meidän on lisättävä nämä todennäköisyyteen, koska ne vähennettiin kahdesti edellisessä vaiheessa. Joten nyt olemme kohdassa 1 - 6*(5/6)^20 + 15*(4/6)^20 = noin 0,84800661.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Jos kuitenkin jokin kolmen sivun ryhmä, jota ei olisi koskaan heitetty, olisi vähennetty kolminkertaisesti ensimmäisessä vaiheessa ja laskettu yhteen kolminkertaisesti toisessa vaiheessa, meidän on vähennettävä ne takaisin tilaan, jossa kaikkia kuutta sivua ei ole heitetty. Kolmen sivun valitsemiseen kuudesta on combin(6,3) = 20 tapaa. Todennäköisyys sille, että mitkä tahansa kolme sivua ei koskaan heitetä, on (3/6)^20. Joten nyt olemme 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 = approks. 0.847987537.

Jos kuitenkin jokin neljän sivun ryhmä, jota ei olisi koskaan heitetty, olisi nelinkertaistettu ensimmäisessä vaiheessa, nelinkertaistettu toisessa vaiheessa ja nelinkertaistettu kolmannessa vaiheessa, meidän on lisättävä ne takaisin, koska jokainen tällainen tila on jo vähennetty kahdesti. On combin(6,4) = 15 tapaa valita neljä sivua kuudesta. Todennäköisyys sille, että mitkä tahansa neljä sivua ei koskaan heitetä, on (2/6)^20. Joten nyt olemme tilanteessa 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = approx. 0.84798754089.

Jos kaikki 20 heittoa olisivat kuitenkin olleet samoja lukuja, tämä tilanne olisi viisinkertaistettu ensimmäisessä vaiheessa, viisinkertaistettu yhteenlaskettu ensimmäisessä vaiheessa, viisinkertaistettu yhteenlaskettu kolmannessa vaiheessa ja viisinkertaistettu yhteenlaskettu neljännessä vaiheessa. Meidän on vähennettävä ne takaisin. Joten nyt olemme 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = noin 0,84798754089.

Eli vastaus on 1-6*(5/6)^20+KOMBIN(6,4)*(4/6)^20-KOMBIN(6,3)*(3/6)^20+KOMBIN(6,2)*(2/6)^20-6*(1/6)^20 = noin 0,84798754089.

Sinulla on kaksi kuutiota. Voit numeroida molempien noppien sivut haluamallasi tavalla, kunhan kumpikin sivu on kokonaisluku ja suurempi tai yhtä suuri kuin yksi. Voit toistaa samaa numeroa samalla nopalla ja nostaa niin korkealle kuin haluat. Tavallisten noppien luomisen lisäksi, miten voit numeroida ne niin, että minkä tahansa annetun kokonaissumman todennäköisyys on sama kuin tavallisilla nopilla?

anonyymi

Noppa 1 = 1, 2, 2, 3, 3, 4.
Noppa 2 = 1, 3, 4, 5, 6, 8.

Pelkäänpä, että ratkaisuni tähän oli pitkälti yrityksen ja erehdyksen kautta tehty.

Kuinka monta heittoa keskimäärin tarvitaan kahdella nopalla, jotta saadaan kaikki yhteistulokset 2:sta 12:een?

anonyymi

Vastaus on 769767316159 / 12574325400 = noin 61,2173847639572.

Tähän voisi käyttää Markov-ketjua, mutta pidän parempana differentiaali- ja integraalilaskentaa. Olennaista on, että vastaus on sama, jos heittojen välinen aika on eksponentiaalisesti jakautunut ja keskiarvo on yksi. Vastaus voidaan kuitenkin ilmaista integraalina nollasta äärettömyyteen:

1-(1-lauseke(-x/36))^2*(1-lauseke(-x/18))^2*(1-lauseke(-x/12))^2*(1-lauseke(-x/9))^2*(1-lauseke(-5*x/36))^2*(1-lauseke(-x/6))

Voit helposti ratkaista tällaiset integraalit integraalilaskimella .

Voit ratkaista minkä tahansa tällaisen ongelman myös odotettavissa olevien kokeiden laskurillani .

Drop Dead on peli, jota pelataan viidellä tavallisella nopalla. Aloitat vuorosi heittämällä kaikki viisi noppaa. Jos mikään niistä ei ole 2 tai 5, lasket noppien summan yhteen, lisäät summan pistemäärääsi ja heität uudelleen. Jos heität mitkä tahansa 2 tai 5, heiton pistemäärä on nolla. Kaikki 2:ta tai 5:tä näyttävät nopat julistetaan kuolleiksi ja sivuun. Sitten heität uudelleen jäljellä olevilla nopilla. Peli jatkuu joko pisteiden keräämisellä tai noppien poistamisella. Vuorosi päättyy, kun kaikki noppasi on pudonnut, jolloin sinun sanotaan kuolleen. Kaikki pisteheittosi lasketaan yhteen lopulliseksi pistemääräksi. Korkea pistemäärä voittaa.

Mikä on odotettu tulos tässä pelissä?

Gialmere

16.064662

Aloitetaan skenaariolla, jossa on yksi noppa jäljellä, ja siirrytään taaksepäin.

Olkoon muuttuja a odotettu lisäpistemäärä, kun jäljellä on yksi noppa.

Keskimääräinen heitto, joka ei ole 2 tai 5, on (1 + 3 + 4 + 6) / 4 = 7/2.

a = (2/3) × (a + 7/2).

a/3 = 7/3.

a = 7.

Lasketaan seuraavaksi b, odotettu pistemäärä, kun jäljellä on kaksi noppaa.

b = (2/3) 2 × (b + 2 × (7/2)) + 2 × (2/3) × (1/3) × a.

b = 11,2.

Lasketaan seuraavaksi c, odotettu pistemäärä, kun jäljellä on kolme noppaa.

c = (2/3) 3 × (c + 3 × (7/2)) + 3 × (2/3) 2 × (1/3) × b + 3 × (2/3) × (1/3) 2 × b.

c = 1302/95 = 13,705263.

Lasketaan seuraavaksi d, odotettu pistemäärä, kun jäljellä on neljä noppaa.

d = (2/3) 4 × (d + 4 × (7/2)) + 4 × (2/3) 3 × (1/3) × c + 6 × (2/3) 2 × (1/3) 2 × b + 4 × (2/3) × (1/3) 3 × a.

d = 3752/247 = 15,190283.

Lopuksi lasketaan e, odotettu pistemäärä, kun jäljellä on viisi noppaa.

e = (2/3) 5 × (e + 5 × (7/2)) + 5 × (2/3) 4 × (1/3) × d + 10 × (2/3) 3 × (1/3) 2 × c + 10 × (2/3) 2 × (1/3) 3 × b + 5 × (1/3) × 4 × (1/3) ×.

e = 16,064662.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Heitä kahta noppaa, punaista ja sinistä noppaa, yhä uudelleen ja uudelleen. Pidä kirjaa kunkin nopan heittojen summasta. Mikä on odotettu roolien lukumäärä, kunnes nämä kaksi yhteissummaa ovat yhtä suuret?

teliot

Vastaus on ääretön.

On vaikea selittää, miksi vastaus on ääretön. Asiaa hämmentää ja tekee paradoksaalisemmaksi se, että todennäköisyys sille, että kokonaissummat koskaan ovat yhtä suuret, on 1.

Seuraava taulukko näyttää todennäköisyyden sille, että kokonaisluvut ovat samat ensimmäistä kertaa 1–16 heiton jälkeen.

Todennäköisyys yhtä suurille kokonaistuloksille ensimmäistä kertaa

Rullat Todennäköisyys
1 0,166667
2 0.112654
3 0,092850
4 0,080944
5 0,072693
6 0,066539
7 0,061722
8 0,057819
9 0,054573
10 0,051819
11 0,049443
12 0,047367
13 0,045532
14 0,043895
15 0,042423
16 0,041089

Excel näyttää erittäin lähellä tätä käyrää olevan kaavan y = 0,1784*x-1,011, jossa x = heittojen lukumäärä ja y = todennäköisyys.

Tämän äärettömän sarjan summa on ääretön.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Viisi punaista ja viisi sinistä noppaa heitetään. Mikä on todennäköisyys, että molempien noppien heitot ovat samat järjestyksestä riippumatta? Esimerkiksi molemmat heitot ovat 1-2-3-3-6.

anonyymi

3 557 / 559 872 = 0,006353238 eli noin 1 / 157.

Seuraava taulukko näyttää minkä tahansa tyyppiselle rullalle:

  • Eri tapojen lukumäärä, joilla tämä heitto voidaan saavuttaa. Esimerkiksi täyskädessä on kuusi yhdistelmää kolmosille ja viisi jäljellä parille, yhteensä 30 erilaista täyskättä.
  • Tilausten lukumäärä. Esimerkiksi täyskäden tapauksessa on combin(5,3)=10 tapaa valita kolme viidestä nopasta kolmosten saamiseksi. Kahdella muulla on oltava pari.
  • Annetun käden saamisen tapojen lukumäärä. Tämä on kahden ensimmäisen sarakkeen tulo. Esimerkiksi täyskäden saamiseen on 30 * 10 = 300 tapaa.
  • Käden todennäköisyys. Esimerkiksi täyskäden todennäköisyys on 300/6 5 = 0,038580.
  • Todennäköisyys sille, että molemmat heitot ovat samoja ja annetulla kädellä, on 0,038580 2 . Todennäköisyys sille, että molemmat heitot ovat täyskäsi, on 0,038580 2 /30 = 0,00004961.

Oikeassa alakulmassa oleva solu näyttää, että molempien heittojen samanarvoisuuden kokonaistodennäköisyys on 0,00635324.

Vastaava rulla

Tyyppi
Rollista		 Eri
Tyypit		 Tilaukset Kokonais
Yhdistelmät		 Todennäköisyys
Yksi rulla		 Todennäköisyys
Kaksi rullaa
Viisi samanlaista 6 1 6 0.00077160 0.00000010
Neloset 30 5 150 0.01929012 0.00001240
Täyskäsi 30 10 300 0.03858025 0.00004961
Kolmoset 60 20 1 200 0.15432099 0.00039692
Kaksi paria 60 30 1 800 0.23148148 0.00089306
Pari 60 60 3 600 0.46296296 0.00357225
Viisi singletonia 6 120 720 0.09259259 0.00142890
Kokonais 7 776 1.00000000 0.00635324

Kuusisivuista noppaa heitetään, kunnes jompikumpi seuraavista tapahtumista tapahtuu:

A) Kumpi tahansa puoli on esiintynyt kuusi kertaa.
B) Jokainen puoli on esiintynyt ainakin kerran.

Mikä on todennäköisyys sille, että tapahtuma A tapahtuu ensin?

Ace2

Vastatakseni tähän kysymykseen kuten minä tein ja käyttäen differentiaali- ja integraalilaskentaa, suosittelen integraalilaskinta, kuten osoitteessa integral-calculator.com/ .

Noin 0,252635881662548

Tässä on ratkaisuni (PDF).

Tätä ongelmaa on kysytty (hieman eri sanoin) ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Haluat pelata peliä, jossa käytetään tavallista kuusisivuista noppaa. Valitettavasti kadotit nopan. Sinulla on kuitenkin neljä indeksikorttia, jotka voit merkitä haluamallasi tavalla. Pelaajan on valittava kaksi korttia satunnaisesti neljästä ilman takaisinpanoa ja laskettava kahden kortin summa.

Kuinka voit numeroida kortit niin, että kahden eri kortin summa edustaa nopanheiton tulosta?

Gialmere

Numeroi ne 0, 1, 2 ja 4.

Neljästä kortista voi nostaa kaksi kuudella eri tavalla.

  • 0+1 = 1
  • 0 + 2 = 2
  • 1 + 2 = 3
  • 0 + 4 = 4
  • 1 + 4 = 5
  • 2 + 4 = 6

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kuusisivuista noppaa heitetään yhä uudelleen, kunnes heittojen summa on 13 tai suurempi. Mikä on loppusumman keskiarvo, mediaani ja moodi?

Gialmere

Keskiarvo = 14,690219
Mediaani = 14
Tila = 13

Minun piti käyttää tähän Markov-ketjua. Seuraava taulukko näyttää kunkin loppusumman todennäköisyyden vasemman sarakkeen juoksevan summan mukaan. Aloita ilmeisistä tapauksista summille 13–18. Sitten juokseville summille 0–12, ota kuuden alla olevan solun keskiarvo.

Alkutilan todennäköisyydet löytyvät ensimmäiseltä riviltä, kun summa on 0.

Markov-ketju

Rolls-summa 13 14 15 16 17 18
0 0,279263 0,236996 0.192313 0,145585 0,097371 0,048472
1 0.290830 0,230791 0.188524 0,143842 0.097114 0,048899
2 0,293393 0,241931 0.181893 0,139625 0,094943 0,048215
3 0.289288 0,245178 0,193717 0,133678 0,091410 0,046728
4 0,280369 0.242560 0.198450 0,146988 0,086950 0,044682
5 0.268094 0,235687 0.197878 0,153768 0.102306 0,042267
6 0,253604 0,225827 0.193419 0,155611 0.111500 0,060039
7 0,360232 0,193566 0,165788 0.133380 0,095572 0,051462
8 0.308771 0.308771 0.142104 0.114326 0,081919 0.044110
9 0,264660 0,264660 0,264660 0,097994 0,070216 0,037809
10 0,226852 0,226852 0,226852 0,226852 0,060185 0,032407
11 0.194444 0.194444 0.194444 0.194444 0.194444 0,027778
12 0,166667 0,166667 0,166667 0,166667 0,166667 0,166667
13 1.000000 0.000000 0.000000 0.000000 0.000000 0.000000
14 0.000000 1.000000 0.000000 0.000000 0.000000 0.000000
15 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000
16 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000
17 0.000000 0.000000 0.000000 0.000000 1.000000 0.000000
18 0.000000 0.000000 0.000000 0.000000 0.000000 1.000000

Tätä kysymystä kysytään ja siitä keskustellaan foorumillani Wizard of Vegas .

Kuten tiedät, craps -pelin All-panos voittaa, jos kaikki luvut 2:sta 12:een, paitsi 7, heitetään ennen 7:n tulosta. Kuinka monta heittoa keskimäärin tarvitaan tämän panoksen voittamiseksi, jos se voittaa?

Ace2

20.989727251191...

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Näen jonkun väittävän, että hänellä on todistajina 18 peräkkäistä pelaajaa (yhteensä 11) craps-pöydässä. Kuinka monta heittoa keskimäärin tarvittaisiin, jotta tuollainen havaittaisiin?

Ace2

41 660 902 667 961 039 785 742 rullaa.

Tässä on ratkaisuni (PDF).

Kahta reilua kuusisivuista noppaa heitetään yhä uudelleen ja uudelleen, kunnes toinen seuraavista kahdesta tapahtumasta tapahtuu:

A) Heitetään yhteensä 12.
B) Yhteensä 7 heitetään kaksi kertaa peräkkäin.

Kumpi tapahtuu todennäköisemmin ensin?

anonyymi

Yhteensä 12.

[spoiler=Ratkaisu]

Olkoon:

  • p = Todennäköisyys, että 12 heitetään ensin lähtötilasta tai milloin tahansa edellinen heitto ei ollut 7.
  • q = Todennäköisyys sille, että numero 12 heitetään ensin, kun edellinen heitto oli 7.

Tätä kutsutaan Markov-ketjun ongelmaksi.

Ennen kuin pääsemme siihen, muista, että todennäköisyys saada yhteensä 7 on 1/6 ja 12 on 1/36.

Voimme määritellä p:n ja q:n toistensa suhteen seuraavasti:

  • (1) p = (1/36) + (6/36)q + (29/36)p
  • (2) q = (1/36) + (29/36)p

Kerrotaan yhtälö (1) luvulla 36:

36p = 1 + 6q + 29p
(3) 7p = 1 + 6q

Sijoitetaan yhtälön (2) q:n arvo yhtälöön (3):

7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13

Joten todennäköisyys sille, että heitetään ensin 12, on 7/13 = ~ 53,85 %.

Todennäköisyys sille, että ensin heitetään kaksi peräkkäistä seiskaa, on siis 46,15 %.

Näin ollen on todennäköisempää, että kokonaisluku 12 heitetään ensin.