Ruletti - Yleisiä kysymyksiä
Jos ruletissa panostetaan kahteen sarakkeeseen, voittotodennäköisyys olisi 24/38 eli 63 %. Tämä vaikuttaa minusta voittavalta strategialta, mitä mieltä olet?
Ruletissa millä tahansa panoksella tai panosyhdistelmällä on korkea talon etu. Mitä todennäköisemmin voitat, sitä enemmän joudut riskeeraamaan suhteessa voittoon. Jos teet tämän 10 kertaa, voiton todennäköisyys on 46,42 %. 100-kertaisella todennäköisyys laskee 24,6 %:iin.
Pidin artikkelistasi peruutusvedonlyöntijärjestelmästä . Millaista peruutusjärjestelmää käyttäisit, jos mustan tai punaisen sijaan panostaisit (saman summan) kahteen kolmesta 12 numeroa kattavasta lohkosta (esim. 1-12 ja 25-36) jokaisella heitolla?
Aloita samalla tavalla kuin selitin tasarahapanoksilla. Jokaisen panoksen tulisi olla vasemman ja oikean numeron summa. Kahden sarakkeen strategiaa noudattaen sinun tulisi kuitenkin lisätä oikealle kaksinkertainen määrä, jos häviät.
Sivustolla www.ccc-casino.com on ruletti ilman nollaa, jota kutsutaan nimellä Super Chance Roulette. Onko olemassa järjestelmiä, jotka olisivat tehokkaita, koska nollaa ei ole? Voisiko ilman nollaa pelata tehokkaasti sekä mustaa että punaista samanaikaisesti, koska nollaa ei tarvitse pelätä?
Pelasin sitä harjoitustilassa ja se vaikuttaa oikealta nollapeliltä. Mikään järjestelmä ei voi joko voittaa tai hävitä tälle pelille pitkällä aikavälillä. Mitä enemmän pelaat, sitä lähemmäksi nettovoiton suhde kokonaispanokseen lähestyy nollaa.
Päivitys: Tämä kasino on sittemmin suljettu.
Kaksi kysymystä sinulle:
1) Blackjackin perusstrategioiden osalta on kyse eri nettikasinoryhmistä. Tarkemmin sanottuna kaksi eri ryhmää, jotka molemmat käyttävät yhtä pakkaa: Microgaming ja Unifed Gaming. En ymmärrä, miksi listaat 11 VS 10 -strategian Microgamingin hittistrategiana, mutta Unifiedin tuplastrategiana. Koska molemmat käyttävät yhtä pakkaa, näyttää siltä, että samaa strategiaa pitäisi käyttää tässäkin. Häviän useammin kuin voitan, kun tuplan tämän.
2) Ruletissa minusta tuntuu, että todennäköisyys olisi panostaa yhtä paljon sekä punaiselle että kolmannelle sarakkeelle tai mustalle ja kolmannelle sarakkeelle. Kolmannessa sarakkeessa on käsittääkseni 8 punaista ja vain 4 mustaa. Toisaalta ensimmäisessä sarakkeessa on enemmän mustia. Pienentääkö tällainen panostaminen talon etua?
Jos tuplaat Microgaming-kasinolla tuloksella 11 ja jakaja saa blackjackin, häviät koko panoksesi. Unified Gamingilla blackjack käännettäisiin välittömästi, jos näkyviin tuleva kortti olisi kymppi, joten tässä tilanteessa ei ole riskiä hävitä blackjackille tuplattaessa.
Kaikki ruletin panosyhdistelmät tuottavat saman odotetun tuoton olettaen, että pelättyä viiden numeron yhdistelmää vältetään. Olet oikeassa siinä, että kolmannessa sarakkeessa on kahdeksan punaista ja neljä mustaa. Todennäköisyys voittaa 3 yksikköä on 8/38, 1 yksikkö on 4/38, break-weight on 10/38 ja hävitä 2 yksikköä on 16/38. Yhdistetty odotettu tuotto yksikköä kohden on (1/2)*(3*8 + 1*4 + 0*10 + 2*16)/38 = -2/38. Jos lyöt vetoa mustasta ja kolmannesta sarakkeesta, todennäköisyys voittaa 3 yksikköä on 4/38, 1 yksikkö on 8/38, break-weight on 14/38 ja hävitä 2 yksikköä on 12/38. Odotustuotto on (1/2)*(3*4 + 1*8 + 0*14 + 2*12)/38 = -2/38. Molemmat yhdistelmät painottavat eri tuloksia eri tavalla, mutta niiden keskiarvo on sama.
Hei Wiz. Olen utelias tietämään, mikä on odotettu pyöräytysten määrä amerikkalaisessa ruletissa ennen kuin kaikki 38 numeroa on valittu ainakin kerran. Onko tämä verrannollinen valintojen määrään (38) vai onko se eksponentiaalisesti verrannollinen tähän lukuun? Yritin selvittää tätä kuusisivuiselle nopalle, mutta jäin nopeasti jumiin.
Kun olet saanut n lukua, todennäköisyys saada uusi luku seuraavalla pyöräytyksellä on (38 - n) / 38. Jos tapahtuman todennäköisyys on p, niin odotettu yritysten määrä ennen kuin se tapahtuu, on 1 / p. Näin ollen odotettu pyöräytysten määrä uuden luvun saamiseksi, olettaen, että sinulla on jo n lukua, on 38 / (38 - n). Esimerkiksi kun olet saanut 20 lukua, odotettu pyöräytysten määrä 21. luvun saamiseksi on 38/18 = 2,11. Joten vastaus on odotettujen pyöräytysten lukumäärän summa kullakin askeleella: (38/38) + (38/37) + (38/36) +... + (38/1) = 160,66.
Mikä olisi todennäköisyys sille, että punainen numero ilmestyy 18 kertaa peräkkäin ruletissa?
(18/38) 18 = ~ 1 luvussa 693745.
Olin kiehtova lukiessani kommenttisi pienten teräspallojen muistittomuudesta. Minulla on kotona rulettipyörä, ja pienet pallot hyppivät riemusta ylös ja alas, kun tulen kotiin sairaalasta. Selvästikin se johtuu siitä, että ne muistavat minut, ja lisäksi luulen, että ne loukkaantuisivat kommenteistasi. Planeetallani ruletti ei ole sallittua, koska pienet pallot voi lahjoa niin helposti. Mielestäni planeettanne haisee, enkä nyt pysty korjaamaan avaruusalustani päästäkseni takaisin kotiin.
Ai niin, ja tuo valkotakkinen mies takanani haluaa sanoa rakastavansa verkkosivustoanne ja olevansa kiitollinen kaikesta työstä, jonka olette tehneet laskelmien esittämiseksi. Hän sanoo, että se on säästänyt hänelle paljon aikaa ja rahaa. Jatkakaa hyvää työtä!
Olen iloinen, että olen auttanut valkotakkista päähenkilöä. Rulettineuvoni rajoittuvat peleihin maan päällä, lahjontaa suositellaan planeetallanne.
Pelasin samaa numeroa 1000 kierrosta peräkkäin 0,00-pyörällä ja osuin kuusi kertaa. Mitkä ovat mahdollisuudet osua kuusi tai vähemmän kertaa tässä tilanteessa?
Todennäköisyys sille, että numerosi osuu täsmälleen x kertaa, on combin(1000,x)*(1/38) x *(37/38) 1000-x . Seuraava taulukko näyttää kaikkien osumien todennäköisyydet välillä 0-6 ja kokonaismäärän.
Voitot 1000 ruletin panoksella
| Määrä | Todennäköisyys |
| 0 | 0.00000000000262 |
| 1 | 0.00000000007078 |
| 2 | 0.00000000095556 |
| 3 | 0.00000000859146 |
| 4 | 0.00000005787627 |
| 5 | 0.00000031159330 |
| 6 | 0.00000139655555 |
| Kokonais | 0.00000177564555 |
Joten vastaus on 0.00000177564555 eli 1/563175. Toivottavasti tämä ei tapahtunut nettikasinolla.
Saatat ihmetellä, miksi en käyttänyt normaalia approksimaatiota kuten yllä olevassa kolikonheittotehtävässä. Tämä johtuu siitä, että se ei toimi hyvin erittäin suurilla ja erittäin pienillä todennäköisyyksillä.
Hei Mike, hieman piristääkseni tunnelmaa, muistan katsoneeni sinun pelaavan rulettia Vegas Challenge -erikoisohjelmassa jonkin aikaa sitten. Tiesit selvästi, että odotusarvosi ei muuttuisi strategiasta riippumatta. Muistan sinun pelanneen vain yhtä numeroa, mutta unohdin, muutitko sitä voiton jälkeen. En ole varma, mitä tekisin sinun tilanteessasi, mutta uteliaisuudesta kysyn, pelasitko yksittäistä numeroa ulkopanoksen, kuten punaisen/mustan, sijaan maksimoidaksesi varianssin? Sillä tavalla, jos olet "onnellinen", olet suurimmalla johdolla? Joka tapauksessa nautin siitä, että pelasit todella konservatiivista ja tylsää strategiaa.
Ymmärsit strategiani varsin hyvin. Aioin panostaa minimin suurimman osan tunnista välttääkseni talon edun lannistamisen. Tuottaja ei ollut tyytyväinen näin tylsään strategiaan, joten yritin esittää innostuneempaa kuin normaalisti olisin. Syy siihen, miksi valitsin yhden numeron tasapelin sijaan, oli se, että halusin volatiliteettia. Tiesin, että jos päätyisin lähelle lähtökohtaani 10 000 dollaria, luultavasti häviäisin. Joten halusin paremmat mahdollisuudet voittaa. Pysyin 23:ssa koko ajan, vaikka loppua kohden lisäsin myös 5. Olen iloinen, että pidit ohjelmasta.
Kysymykseni perustuu enemmän sinun havaintoihin ja itse kuulemiini huhuihin. Jos on totta, että Las Vegasin jakajat oppivat jakajakoulussa pyörittämään ja vierittämään palloa samalla tavalla, niin onko totta, että jakajan pyöräytystä tarkkailemalla voidaan määrittää, mille pyörän neljännekselle pallo saattaa pysähtyä?
Ei. Jakajille opetetaan vain perusasiat eikä läheskään niin taitavia asioita. Itse asiassa, jos jakajalla olisi tuo määräysvalta, hän voisi yksinkertaisesti saada rikoskumppaninsa panostamaan mihin tahansa hän suunnitteli pallon laskeutuvan, ja he voisivat helposti tienata miljoonia.
Mitkä ovat todennäköisyydet pelata eurooppalaista rulettia 15 pyöräytyksellä, kattaa kahdeksan numeroa ja jäädä paitsi yhdestäkään niistä?
Yhden pyöräytyksen häviämisen todennäköisyys on 1-(8/37) = 78,38 %. Joten 15 pyöräytyksen häviämisen todennäköisyys on 0,7838, 15 = 2,59 %.
Haluaisin tietää, miten testata nettirulettipeliä, tietää kertoimet ja ovatko ne rehellisiä?
Ensin kerron, miten pelejä ei kannata testata. Sinun ei pitäisi tallentaa kaikkea peliäsi ja etsiä sitten poikkeavuuksia, ja sitten kirjoittaa minulle valittaen, että kasino huijaa. Oikea tapa on esittää hypoteesi siitä, miten kasino huijaa ENSIN, sitten kerätä tietoja ja lopuksi katsoa, vastaavatko tiedot hypoteesiasi. Jos et tiedä, millaisen hypoteesin esittää, ehdotan, että testaat yksinkertaisesti voittojen ja tappioiden määrää ja panostat sitten saman summan joka kerta. Jos teet kaksi ensimmäistä vaihetta oikein ja tarvitset apua kolmannessa, kirjoita minulle.
Kun menen kasinolle 100 dollarin kanssa ja pelaan rulettia, en odota poistuvani sieltä 4 % halvemmalla, vaan 25 % halvemmalla. Onko tällä ilmiöllä virallinen nimi? (Googlasin "todellinen talon etu") Onko olemassa mitään kaavaa/mallia tämän "todellisen talon edun" ennustamiseksi? Mitkä pelit ovat parempia ja mitkä huonompia tässä parametrissa?
Esimerkissäsi kasinon pidätysprosentti on 75 %. Se on pelaajien pois saamien pelimerkkien arvon suhde jakajan laatikkoon pudottaman rahamäärään. Vaikka historiallisia keskiarvoja on olemassa, ei ole mitään keinoa siirtyä talon edusta pidätysprosenttiin. Pidätysprosentti riippuu osittain siitä, kuinka kauan pelaaja kierrättää pelimerkkejään, eikä sitä voi tietää.
Jos minulla on 200 dollarin pelikassa, jonka häviäminen ei haittaa, ja jatkan 10 dollarin pelaamista yhdellä numerolla eurooppalaisessa (yhden nollan) ruletissa, mitkä ovat todennäköisyydet voittaa 200 dollaria, 500 dollaria vai 1000 dollaria? Olettaen, että lopetan tavoitteen saavuttamisen jälkeen. Kiitos, hieno sivusto, halusit minun pitävän tämän lyhyenä :)
Kiitos kohteliaisuudesta. Tällaisiin kysymyksiin on olemassa kaava, jonka selitän sivustollani www.mathproblems.info , katso tehtävä 116.
Jos pelikassasi on b yksikköä, voittotavoite on g yksikköä, voiton todennäköisyys on p ja häviön todennäköisyys on q, onnistumisen todennäköisyys on ((q/p) b -1)/((q/p) b+g -1). Tässä tapauksessa b=20, p=18/37, q=19/37 ja g=20, 50 ja 100. Joten 200 dollarin pelikassalla todennäköisyys on ((19/18) 20 -1)/((19/18) 40 -1) = 0,253252.
500 dollarin voittomaalin todennäköisyys on ((19/18) 20 -1)/((19/18) 70 -1) = 0,045293.
1 000 dollarin voittomaalin todennäköisyys on ((19/18) 20 -1) / ((19/18) 120 -1) = 0,002969.
38 numeron rulettipyörällä... kun saat kolme punaista, yhden vihreän ja sitten toisen punaisen... mitkä ovat todennäköisyydet, että seuraavat kolme peräkkäistä pyöräytystä ovat punaisia ja numero 23?
Sillä ei ole väliä, mitä aiemmat pyöräytykset olivat. Todennäköisyys sille, että punaista 23 tulee kolme kertaa peräkkäin, on (1/38) * 3 = 1/1/54 872.
Kävin Bodogilla ja kokeilin heidän rulettipyöräänsä ilmaisella sivustolla. Yläkulmassa olevaan laatikkoon tallentuvat kymmenen viimeisintä osunutta numeroa. Pyöräytin sitä varmasti alle 20 kertaa. Tallennetut numerot ovat seuraavat: 9-9-29-21-11-11-20-28-32-1 Mielenkiintoista kyllä, kaksi pyöräytystä aiemmin osui toinen numero numeroon 32. Tämä tarkoittaa, että numerot 9, 11 ja 32 osuivat kaikki kahdesti 12 pyöräytyksen aikana. Kuten sanoin, en ole tilastotieteilijä, mutta näiden kolmen numeron esiintymistiheys yhdistettynä pyöräytyskertojen vähäiseen määrään näyttää viittaavan siihen, että jokin on vialla.
Kolmen parin ja kuuden yksittäisen symbolin todennäköisyys kahdessatoista pyöräytyksessä on combin (38,3) × combin(35,6) × combin(12,2) × combin(10,2) × combin(8,2) × fact(6)/38 12 = 9,04 %. Laskelma menee melko sekavaksi kysyttäessä todennäköisyyttä sille, että tämä voisi tapahtua millä tahansa 12 pyöräytyksen jaksolla 20 pyöräytyksen kokonaismäärän aikana. Riittää, kun sanon, että se on huomattavasti enemmän kuin 9 %, todennäköisempi kuin ei, veikkaan. Joten nämä vaikuttavat minusta hyvin normaaleilta tuloksilta.
Yksi kotikaupunkini kasinoista maksaa 36:1 suorasta panoksesta yhden nollan rulettipyörällä tietylle numerolle sinä päivänä. Esimerkiksi tietty numero on 8 kuukauden 8. päivänä. Miten se muuttaa talon etua? Kiitos avustasi.
Talon etu annetulla numerolla olisi täsmälleen 0 %.
Orleansissa on ruletissa sivupanos, joka maksaa voittoja 8:1 kolmella punaisella (tai mustalla) peräkkäin. Se on tuplanolla-pyörällä. Voitko kertoa minulle kertoimet?
Voiton todennäköisyys on (18/38) 3 = 10,63 %. Talon etu on 8 × 0,1063 - 1 × 0,8937 = 4,34 %, mikä on vähemmän kuin kaikkien muiden vetojen 5,26 % (paitsi pelätyn 0,00,1,2,3-yhdistelmän, jonka todennäköisyys on 7,89 %).
Jotkut hollantilaiset kasinot sallivat kolminkertaisen vankeusrangaistuksen ruletissa. Mikä on talon etu tasarahapanoksissa tämän säännön nojalla? Olen kiinnostuneempi ratkaisusta kuin vastauksesta.
Muiden lukijoiden tiedoksi, monissa eurooppalaisissa kasinoissa ruletissa panostetaan tasarahalla, jos kuula pysähtyy nollaan. Jos seuraava heitto toisi voiton, panos palautetaan ilman voittoja. Jos kuula pysähtyy vastakkaiseen suuntaan, panos häviää.
Mitä tapahtuu kertavankeuspanoksille, jos pallo pysähtyy nollaan? Jos kasino sallii vain kertavankeusrangaistuksen, se häviää. Jotkut kasinot kuitenkin sallivat kaksinkertaisen vankeusrangaistuksen, ja näin tapahtuukin. Jos kaksinkertaisella vankeusrangaistuksella tehty panos voittaa, se palaa kertavankeusrangaistukseen. Jos kasino sallii vain enintään kaksinkertaisen vankeusrangaistuksen, kaksinkertaisella vankeusrangaistuksella tehty panos häviää toisella nollalla. Samalla logiikalla, jos kasino sallii kolminkertaisen vankeusrangaistuksen, kaksinkertaisella vankeusrangaistuksella tehty panos muuttuu kolminkertaiseksi vankeusrangaistukseksi toisella nollalla.
Talon etu kolmoisvankeusrangaistuksessa on 1,370120 %. Ennen kuin selitän, miten päädyin tähän, tarkastellaan ensin yksi- ja kaksinkertaista vankeusrangaistusta. Oletetaan, että ensimmäinen panos on punaiselle.
Olkoon Z = nollan todennäköisyys = 1/37.
Olkoon R = punaisen luvun todennäköisyys = 18/37.
Yksittäinen vankeusrangaistus
pr(työntö) = ZR = 0,0131482834.
pr(voitto) = R = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5003652301.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0138787436.
Kaksinkertainen vankeusrangaistus
Pelaaja työntää, jos ensimmäinen pyöräytys on nolla, niin pelaaja voi toistaa ZR:n nollasta äärettömän monta kertaa ja saada sitten punaisen. Toisin sanoen, työntämisen tavat ovat:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
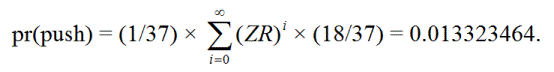
pr(työntö) = 0,013323464
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001900494.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137035629.
Kolminkertainen vankeusrangaistus
Etsitään ensin todennäköisyys p 1 sille, että yksinkertaisesti vangittu veto muuttuu kolminkertaisesti vangituksi kahdella nollalla lisää ja lopulta nousee takaisin yksinkertaisesti vangituksi. Tämä voi tapahtua seuraavasti:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
Toisin sanoen panos voi vaihdella kolminkertaisen ja kaksinkertaisen vangitsemisen välillä jopa äärettömän monta kertaa.
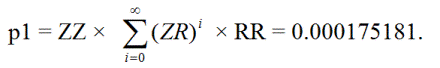
Toiseksi, olkoon p 2 = todennäköisyys sille, että yksittäinen vankeusrangaistus saavuttaa ensimmäisen tai toisen vankeusrangaistustason ja palaa sitten yksittäiseen vankeusrangaistukseen.
Olkoon p² = ZR + p¹ = 0,013323464.
Pelaaja voi palata ensimmäiselle tasolle nollasta äärettömän monta kertaa. Joten puskemisen todennäköisyys on:
ZR + Zp 2R + Zp 2p 2R + Zp 2p 2R + ... =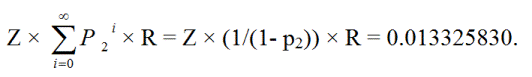
Z × (1/(1 - p2 )) × R = 0,013325830.
pr(työntö) = 0,013325830.
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001876839.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137011974.
Ääretön vankeus
Ei niin, että kysyit, Maff, mutta kuulin, että Espanjassa sallitaan ääretön vangitseminen. Olkoon p = työntötodennäköisyys. Tämä on myös todennäköisyys aloittaa vangitsemisen tasolta x, pudota syvemmälle tasoille ja lopulta kiivetä takaisin tasolle x.
p = ZR + ZpR + ZppR + ZpppR + ...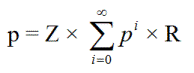
p2 - p + ZR = 0
Toisen asteen kaavan mukaan p = (1-(1-4*RZ) ^1/ 2)/2 = 0,0133258620.
pr(työntö) = 0,0133258620.
pr(voitto) = 18/37 = 0,4864864865.
pr(tappio) = 1-pr(push)-pr(voitto) = 0,5001876515.
Odotusarvo = pr(voitto) - pr(tappio) = -0,0137011650.
Nollat jättivät vankeusrangaistuksen huomiotta
Lopuksi, joissakin kasinoissa nollat yksinkertaisesti jätetään huomiotta ensimmäisen nollan jälkeen, mikä vangitsee panoksen. Näissä tasapelin todennäköisyys on yksinkertaisesti (1/37) × (1/2) = 0,0135135135.
Seuraavassa taulukossa on yhteenveto kaikista neljästä sääntötyypistä.
Vankeusrangaistuksen kertoimet
| Vankeusrangaistus | Voittaa | Työnnä | Menetys | Odotettu Arvo |
| Yksittäinen | 0.48648649 | 0.01314828 | 0.50036523 | -0,01387874 |
| Kaksinkertainen | 0.48648649 | 0.01332346 | 0.50019005 | -0,01370356 |
| Kolminkertaistaa | 0.48648649 | 0,01332583 | 0.50018768 | -0,01370120 |
| Ääretön | 0.48648649 | 0,01332586 | 0.50018765 | -0,01370117 |
| Nollat jätetään huomiotta | 0.48648649 | 0.01351351 | 0,50000000 | -0,01351351 |
Haluan kiittää ChesterDogia ja weaselmania heidän matemaattisesta avustaan. Haluan myös kiittää ja suositella professori G. Articoa ja polarprof.it-sivustoa yllä olevan summakaavan HTML-koodista.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Onko rulettipyörän numeroiden järjestyksessä jokin kaava?


Ajatuksena on, että pyörän tulisi olla tasapainossa. Toisin sanoen, jos ottaisit keskiarvon useista peräkkäisistä numeroista pyörällä, ne olisivat lähellä keskiarvoa 18,5. Keksin tavan selittää numeroiden jakautumista tuplanolla-pyörällä seuraavasti.
- Sijoita 00 kello 12:00 kohtaan ja 0 kello 6:00 kohtaan.
- Pyörän yläosassa olevat numerot ovat 13, 1, 00, 27, 10*, 25. Tämä täytyy yksinkertaisesti opetella ulkoa.
- Kaikki pienet parittomat numerot (1–17) ovat vasemmalla puolella ja suuret kertoimet (19–35) oikealla puolella.
- Aloita numeroista 1 ja 13 ja siirry neljä asentoa vastapäivään saadaksesi seuraavan parittoman numeron, mutta älä ylitä nollaa.
- Poikkeuksena säännöstä 4, älä aseta numeroa 19 neljään kohtaan vastapäivään numerosta 17, koska 19 on korkea pariton ja kuuluu oikealle puolelle. Sen sijaan aseta numero 11, joka on ainoa matala pariton, jota sääntö 4 ei muuten kata.
- Kaikki parilliset numerot ovat suoraan pyörän poikki, 180 astetta, edellisestä parittomasta numerosta.
En osaa selittää yhden nollan ruletin järjestystä. Tällä hetkellä voin sanoa, että jos nolla sijoitetaan klo 12:00, niin:
- Vasemmalla puolella ovat punaiset matalat numerot ja mustat korkeat numerot.
- Oikealla puolella ovat punaiset korkeat numerot ja mustat matalat numerot.
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Seurasin 3 000 pyöräytystä tuplanolla-ruletissa, koska ensimmäiset tusinat eivät näyttäneet ilmestyvän yhtä usein kuin seuraavat kaksi tusinaa. 3 000 pyöräytyksellä numerot väliltä 1–12 ilmestyivät 742 kertaa. Mikä on tämän todennäköisyys?
Odottaisit, että pallon laskeutumiskertojen määrä välillä 1–12 olisi 3000 * (12/38) = 947,37.
Tulostesi ja odotustesi välinen ero on 947,37 - 742 = 205,37.
Varianssi on 3000*(12/38)*(1-(12/38)) = 648,20.
Keskihajonta on varianssin neliöjuuri = sqrt(648,20) = 25,46.
Tuloksesi ovat 205,37/25,46 = 11,75 keskihajontaa odotuksen eteläpuolella.
P-arvo eli todennäköisyys sille, että poikkeama on 11,75 keskihajontaa tai enemmän, on 1/28 542 806 257 940 300 000 000 000 000 000.
Kiinnostaisi tietää, missä ratti on.
Mitä mieltä olet Comp Killer -rulettistrategiasta, jota käsitellään tässä videossa ?
On helppo nähdä, että kyseisen järjestelmän tarkoituksena on kattaa useimmat numerot, joten se on melko vähäriskinen tapa pelata rulettia. Tässä on panostussummat kullakin pyöräytyksellä:
- 5 dollaria kappaleelta numeroista 3, 16, 24, 28 ja 33.
- Aseta kulmapanos jokaiselle näistä numerosarjoista: 2/3/5/6, 7/8/10/11, 14/15/17/18, 19/20/22/23, 26/27/29/30, 31/32/34/35.
Huomaa, että tämä ei kata seuraavia yhdeksää numeroa: 0, 00, 4, 9, 12, 13, 21, 25 ja 36.
Seuraava tuottotaulukko näyttää kaikkien mahdollisten tulosten todennäköisyyden ja osuuden tuotossa.
Comp Killer
| Tapahtuma | Nettovoitto | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|---|
| Suora voitto | 5 | 5 | 0,131579 | 0,657895 |
| Kulmavoitto | 50 | 24 | 0,631579 | 31.578947 |
| Kaikki muut | -175 | 9 | 0,236842 | -41,447368 |
| Kokonais | 38 | 1.000000 | -9,210526 |
Oikeassa alakulmassa näkyy odotettu tappio 9,21 dollaria kierrosta kohden. Kokonaispanos kierrosta kohden on 175 dollaria. Tämä johtaa talon etuun 9,21 dollaria / 175 dollaria = 5,26 %, joka on talon etu tuplanolla-ruletissa.
Haluaisin lisätä, että todennäköisesti häviät enemmän kuin saat takaisin comp-vedoissa tällä strategialla tai millä tahansa rulettistrategialla. Nyrkkisääntönä on, että kasinot antavat sinulle takaisin noin 1/3 odotetusta tappiostasi comp-vedoissa. On olemassa tapoja huijata kasinoita sillä, että odotettu tappiosi on suurempi kuin se todellisuudessa on, mutta tämän strategian pelaaminen ei ole yksi niistä.
Mitä mieltä olet tästä rulettistrategiasta?
- Panosta kaksi yksikköä mustalle
- Lyö vetoa yhdestä yksiköstä kolmanteen sarakkeeseen
Tämän strategian kauneus piilee siinä, että kolmannessa sarakkeessa on 8 punaista ja 4 mustaa numeroa. Kuudestatoista punaisesta numerosta puolet on sarakkeissa 1 tai 2 ja puolet sarakkeessa 3. Jätetään 0 ja 00 nyt huomiotta. Kun pallo pysähtyy punaiseen, 18 punaisesta numerosta 8 on kolmannessa sarakkeessa. Jos voittotodennäköisyys on 8/18 ja voitot maksavat suhteessa 2:1, pelaajaetuni on 33,3 %. Vaikka keskiarvoistaisimme sen panoksella mustalle ja talon edulla 0 %, jälleen jättäen 0 ja 00 nyt huomiotta, pelaajaetuni on silti 16,7 %. Eikö 0:n ja 00:n yhdistäminen ole etuni (2/38)*-100 % + (36/38)*16,7 % = 10,53 %! Mitä mieltä olet?
Olen samaa mieltä siitä, että kolmannen sarakkeen panoksen ehdollinen etu on 33,3 % olettaen, että pallo pysähtyy punaiseen, ja jättäen molemmat nollat huomiotta. Samalla logiikalla, jos pallo pysähtyy mustaan, kolmannen sarakkeen panoksen voittotodennäköisyys on 4/18 = 2/9. Panoksella, jonka voittomahdollisuus on 2/9 ja jonka voittosuhde on 2:1, talon etu olisi 33,33 %. Joten sinun näkökulmastasi kolmannen sarakkeen panoksella olisi pelaajan etu 33,33 % puolet ajasta ja talon etu 33,33 % toisella puolella ajasta. Jos nämä kumoavat toisensa, talon etu on 0 %. Lopuksi, jos kaksi nollaa lisätään, pelaajan kokonaisetu on (2/38)*-100 % + (36/38)*0 % = -5,26 %.
Toisesta näkökulmasta katsottuna seuraava taulukko näyttää kaikkien mahdollisten tulosten tapahtumistapojen lukumäärän, todennäköisyyden, voitettujen yksiköiden määrän ja niiden vaikutuksen tuottoon. Oikeassa alakulmassa oleva solu näyttää odotetun tappion -0,105263 yksikköä. Jaettuna kahdella panostetulla yksiköllä saadaan talon etu 5,26 %.
Bohemian strategia
| Tapahtuma | Maksaa | Numerot | Todennäköisyys | Palata |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0,052632 | -0,105263 |
| Punainen ja sarake 1 tai 2 | -2 | 10 | 0,263158 | -0,526316 |
| Punainen ja sarake 3 | 1 | 8 | 0,210526 | 0,210526 |
| Musta ja sarake 1 tai 2 | 0 | 14 | 0.368421 | 0.000000 |
| Musta ja sarake 3 | 3 | 4 | 0,105263 | 0,315789 |
| Kokonais | 38 | 1.000000 | -0,105263 |
Mikä on odotettu kierrosten määrä, joka tarvitaan viiden punaisen tai viiden mustan saamiseksi peräkkäin?
Tässä on ratkaisuni (PDF).
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Kuulin, että nelinkertaisen nollan ruletti on nyt saatavilla. Mikä on talon etu?

Kyllä, TCS John Huxley markkinoi tällaista kiekkoa. En ole vielä tietoinen mistään sijoitteluista.
Tavallisessa ruletissa talon edun kaava on z/(36+z), jossa z = nollien lukumäärä. Tässä tapauksessa talon etu on 4/(36+4) = 4/40 = 1/10 = 10 %.


