Tällä sivulla
Miksi korttipakkojen määrällä on merkitystä blackjackissa
Johdanto
Mikä tahansa luotettava blackjack-lähde väittää, että blackjackissa käytettyjen pakkalukumäärän ja talon edun välillä on positiivinen korrelaatio, kun kaikki muut tekijät pysyvät samoina. Toisin sanoen, mitä vähemmän pakkalukuja on, sitä paremmat ovat voittomahdollisuudet harrastelijapelaajalla. Tämä tosiasia on yleistä blackjackin pelaajien keskuudessa, jotka ovat ainakin tarpeeksi asiantuntevia vertaillakseen peliä hyvillä säännöillä. En kuitenkaan ole koskaan nähnyt perusteellista selvitystä siitä, miksi tämä on totta. Tämän artikkelin tarkoituksena on valaista tätä kysymystä.
Ennen kuin aloitan, haluan esittää joitakin perussääntöjä. Ne valittiin mahdollisimman realistisiksi ottaen huomioon blackjackin olosuhteet kirjoitushetkellä vuonna 2020:
- Jakaja lyö pehmeän 17.
- Blackjack maksaa voittosuhteen 3:2.
- Jakaja kurkistaa blackjackin varalta, jolla on kympin tai ässä näkyvissä.
- Pelaaja voi tuplata millä tahansa kahdella kortilla.
- Pelaaja ei saa luovuttaa.
- Pelaaja voi tuplata jaon jälkeen.
- Pelaaja voi jakaa minkä tahansa parin (ässät mukaan lukien) uudelleen enintään kolme kertaa.
- Jatkuvasti sekoittavaa korttia käytetään (kortit sekoitetaan jokaisen käden jälkeen).
- Pelaaja käyttää perusstrategiaa.
Blackjackin talon edun laskurini osoittaa, että näiden sääntöjen mukaan talon etu on seuraava pakkojen lukumäärän mukaan:
Blackjack House Edge Decksin toimesta
| Kannet | Talon etu |
|---|---|
| 1 | 0,014 % |
| 2 | 0,341 % |
| 4 | 0,499 % |
| 6 | 0,551 % |
| 8 | 0,577 % |
Nämä luvut eivät välttämättä ole täysin samat kuin muissa arvostetuissa blackjackia käsittelevissä lähteissä. Uskon, että mahdolliset erot johtuvat joko jaetun kortin käytöstä tai pelaajan käyttämästä optimaalisesta, yhdistelmästä riippuvasta strategiasta. Vertailun vuoksi oletan, että kortit sekoitetaan jokaisen käden jälkeen ja pelaaja noudattaa aina kokonaissummasta riippuvaa perusstrategiaa.
Huomaa, että talon etu on 0,563 % kahdeksan ja yhden pakan välillä. Tässä artikkelissa pyritään vastaamaan kysymykseen, miksi pakkojen lukumäärällä on niin merkittävä vaikutus kertoimiin.
Tasapainoinen peli
Lähtökohtana tarkastelen yksinkertaistettua blackjack-peliä, jossa säännöt ovat täsmälleen samat sekä pelaajalle että jakajalle, jolloin talon etu on 0 % pakkojen lukumäärästä riippumatta. Sitten lisään vähitellen varsinaiset blackjackin säännöt yksi kerrallaan ja tarkastelen, miten ne vaikuttavat talon etuun pakkojen lukumäärän mukaan.
Alkuperäisessä hypoteettisessa yksinkertaistetussa blackjack-pelissä on samat säännöt kuin aiemmin mainittiin, paitsi että:
- Pelaaja noudattaa "jäljittele jakajaa" -strategiaa.
- Blackjackin voittaminen maksaa tasarahat.
- Jos sekä pelaaja että jakaja menettävät kätensä, tuloksena on tasapeli.
Talon etu tässä tasapainotetussa pelissä on ilmiselvästi tasan 0,000 %, koska jokainen sääntö on yhtäläinen molempiin suuntiin.
Jälleenmyyjän asemaetu
Kumpi voittaa blackjackissa, kun sekä pelaaja että jakaja häviävät? Jakaja voittaa. Toisin sanoen jakajalla on asemaetu siinä mielessä, että ensimmäisenä häviävä häviää ja pelaajan on toimittava ensin. Tästä syystä jakajalla on etu, huolimatta monista säännöistä, jotka rajoittavat pelaajan tietä. Tämän säännön lisääminen tasapainopeliin ja sen simulointi yhden ja kahdeksan pakan kanssa johtaa seuraaviin odotettuihin tuottoihin pelaajalle.
Säännön muutoksen odotusarvot
| Sääntö | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Jälleenmyyjän asemaetu | -8,237 % | -8,157% | -0,079 % |
Yllä oleva taulukko osoittaa, että tässä hypoteettisessa pelissä, jossa on yksi pakka, todennäköisyydet pelaajalle ovat huonommat kuin kahdeksalla pakalla. Tämä johtuu siitä, että pakkojen määrän pienentyessä häviämisen todennäköisyys kasvaa. Seuraavassa on häviämisen todennäköisyys tässä "jakajan jäljittely" -pelissä olettaen, että jakaja pelaa kätensä loppuun, vaikka pelaaja häviäisi ensin.
- Yksi pakka = 27,333 %
- Kahdeksan pakkaa = 27,209 %
Yllä oleva osoittaa, että kummankin osapuolen putoamisen todennäköisyys on 0,124 % suurempi yhden pakan pelissä verrattuna kahdeksan pakan peliin. Kummankin osapuolen putoamisen välillä on jonkin verran korrelaatiota, joten tarkastellaan kaikkia neljää pelaajan ja jakajan putoamisen yhdistelmää:
Bushin todennäköisyydet
| Pelaajan rintakuva | Jälleenmyyjän tappio | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|---|
| Ei | Ei | 44,096 % | 44,468 % | -0,372% |
| Ei | Kyllä | 19,095 % | 19,051 % | 0,044 % |
| Kyllä | Ei | 19,095 % | 19,051 % | 0,044 % |
| Kyllä | Kyllä | 8,237 % | 8,157 % | 0,079 % |
| Kokonais | 90,524 % | 90,728 % | -0,204% |
Syy siihen, miksi todennäköisyyksien summa ei ole 100 %, on se, että pöydässä ei lasketa niitä käsiä, joissa kummallakin puolella on blackjack ja kättä ei muuten pelata loppuun. "Kyllä Kyllä" -rivi näyttää tilanteet, joissa molemmat osapuolet menevät yli, jolloin jakaja voittaa. Se osoittaa, että tämä tapahtuu 0,080 % useammin yhden pakan pelissä verrattuna kahdeksan pakkaan. Miksi? Jos kumpi tahansa puoli menee yli, sen on täytynyt tapahtua 12–16 pisteen kovan käden saamisen jälkeen. Tämän käden on täytynyt koostua vähintään kahdesta kortista. Jos jommallakummalla puolella on kaksi korkean arvon korttia, se pysyy voimassa. Toisin sanoen, voittaminen tapahtuu yleensä käsillä, joilla on keskimääräistä pienempiä kortteja. Tämä pienten korttien poistaminen voittamistasoissa aiheuttaa sen, että jäljellä olevilla korteilla on ylijäämä korkeita kortteja. Tämä pienten korttien poistamisen vaikutus ennen voittamista on merkittävämpi yhden pakan pelissä.
Blackjack voittaa 3:2
Seuraava tasapainotettuun peliin lisättävä sääntö on, että blackjackin voittava pelaaja maksaa voittosuhteella 3:2. Tämän säännön lisääminen simulaatiooni johtaa seuraaviin kumulatiivisiin pelaajan odotettuihin tuottoihin.
- Yksi pakka = -5,912 %
- Kahdeksan pakkaa = -5,894 %
Simulaatiotulostaulukko, johon lisätään rivi tämän säännön lisäämistä varten, on seuraava:
Säännön muutoksen odotusarvot
| Sääntö | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Jälleenmyyjän asemaetu | -8,237 % | -8,157% | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | -5,912 % | -5,894% | -0,018% |
Kahden rivin välinen ero osoittaa pelaajan hyödyn, jos blackjackissa on voittosuhde 3:2:
- Yksi pakka = 2,325 %
- Kahdeksan pakkaa = 2,263 %
- Ero = 0,062 %
Tämä on helppo todentaa matemaattisesti seuraavasti. Olkoon d = pakkamäärä. Excel-merkintämuotoa käyttäen blackjackin voittotodennäköisyys on: todennäköisyys(pelaajan blackjack) * (1 - todennäköisyys(jakajan blackjack)) = (16*d)*(4*d)/yhdistelmä(52*d,2) * [1-(16*d-1)*(4*d-1)/yhdistelmä(52*d-2,2)
Blackjackin voittotodennäköisyys
| Kannet | Todennäköisyys |
|---|---|
| 1 | 4,649 % |
| 2 | 4,578 % |
| 4 | 4,544 % |
| 6 | 4,532 % |
| 8 | 4,527 % |
Kuten yllä on nähty, blackjackin voittotodennäköisyys kasvaa pakkojen määrän vähentyessä. Tämä johtuu yksinkertaisesti korttien poistamisen vaikutuksista. Oletetaan esimerkiksi, että ensimmäinen pelaajakortti on mikä tahansa 10-arvoinen kortti. Tämän todennäköisyys on 4/13 pakkojen lukumäärästä riippumatta. On helppo nähdä, että yhden pakan pelissä ässän saamisen todennäköisyys toisena korttina on 4/51 = 7,843 %. Kahdeksan pakan pelissä tämä todennäköisyys on 32/415 = 7,711 %, mikä on 0,123 % vähemmän kuin yhden pakan pelissä. Yksinkertaisesti sanottuna ässän saamisen todennäköisyys on suurempi yhden pakan pelissä siksi, että pakassa on enemmän ässiä, kun siitä poistetaan 10. Sama pätee, jos ensimmäinen kortti on ässä; jäljellä olevissa korteissa on enemmän kymmeniä yhden pakan pelissä.
Lisäksi, jos pelaaja saa blackjackin, jakajan todennäköisyys saada blackjack pienenee pakkojen määrän vähentyessä. Tämä johtuu siitä, että pelaajan poistama ässä ja kymppi pakasta yhden pakan pelissä tekee jakajan blackjackin saamisesta paljon vaikeampaa verrattuna kahdeksan pakan peliin. Tarkemmin sanottuna jakajan blackjackin todennäköisyys, olettaen, että pelaajalla on jo blackjack, on 3,673 % yhdellä pakalla ja 4,605 % kahdeksalla pakalla. Pelaaja voittaa ylimääräisen puoli yksikköä jokaisella voittavalla blackjackilla. Saadaksesi voittavan blackjackin arvon, joka maksaa hypoteettisessa tasapainoisessa pelissämme 3-2, kerrotaan voittoblackjackin todennäköisyys 0,5:llä joka kerta, kun ylimääräinen puoli yksikköä on saavutettu. Tämä johtaa pelaajan etuun pakkojen lukumäärän mukaan seuraavasti:
Pelaajan etu blackjackin voittamisesta
| Kannet | Pelaajan reuna |
|---|---|
| 1 | 2,325 % |
| 2 | 2,289 % |
| 4 | 2,272 % |
| 6 | 2,266 % |
| 8 | 2,263 % |
Huomaa, että voittavan pelaajan blackjackin ylimääräisen puolikkaan yksikön maksamisen matemaattisesti lasketut hyödyt vastaavat aiemmin yhden ja kahdeksan pakan kohdalla esitettyjä simulaatiotuloksia.
Alla oleva taulukko näyttää tähän mennessä analysoitujen sääntöjen juoksevan luettelon ja niiden hyödyt yhden pakan pelaajalle verrattuna kahdeksan pakkaan:
Sääntöjen vaikutus
| Sääntö | Yhden kannen etu |
|---|---|
| Jälleenmyyjän asemaetu | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | 0,062 % |
| Kokonais | -0,018% |
Seuraavaksi analysoidaan, mitä hyötyä pelaajalle on siitä, että hän voi jäädä kovaan kokonaissummaan 12–16. Kokonaissummasta riippuva perusstrategia tällä alueella on sama mille tahansa määrälle pakakoita seuraavasti:
- Jos pisteitä on yhteensä 12, jää seisomaan jakajaa vastaan 4–6 kertaa, muuten ota kortti.
- Jos pistemäärä on 13–16, jää seisomaan jakajaa vastaan, jolla on pistemäärä 2–6, muuten otat kortin.
Tämän strategian lisääminen simulaatioon johtaa seuraaviin pelaajan odotettuihin tuottoihin:
- Yksi pakka = -2,209%
- Kahdeksan pakkaa = -2,625 %
Alla oleva simulaatiotulostaulukko sisältää rivin tämän säännön lisäämistä varten:
Odotusarvot säännön muutoksen mukaan
| Sääntö | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Jälleenmyyjän asemaetu | -8,237 % | -8,157% | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | -5,912 % | -5,894% | -0,018% |
Toisen ja kolmannen rivin välisen eron tarkastelu osoittaa, miten pelaajalla on vapaa tahto jäädä vaikeaan 12–16-tulokseen.
- Yksi pakka = 3,703 %
- Kahdeksan pakkaa = 3,270 %
- Ero = 0,433 %
Näiden kahden luvun erotus osoittaa, että tämän sääntömuutoksen vaikutus on pelaajalle 0,433 % arvokkaampi yhden pakan pelissä verrattuna kahdeksan pakkaan. Toisin kuin yleisesti uskotaan, tämä selittää suurimman osan siitä, miksi yhden pakan peli on pelaajalle 0,563 % arvokkaampi kuin kahdeksan pakan peli.
Tarkastellaan tarkemmin, mitä tapahtuu, kun pelaaja jää jäykillä kokonaispisteillä 12–16, kun taas jakaja ei voi – tämä taulukko näyttää pelaajan hyödyt eri tapahtumista, jotka muuttuvat pelaajan saadessa vähemmän jäykkiä kokonaispisteitä, mikä johtaa vähemmän pelaajien ja useampien jakajan tappioiden tapahtumiseen sekä jakajan häviämiin enemmän aloituksia:
Mahdollisia tuloksia, kun pelaaja jää vaikeusasteille 12–16
| Tapahtuma | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Vähemmän vain pelaajien tekemiä tappioita | 6,282 % | 6,271 % | 0,010 % |
| Lisää vain jakajien tekemiä tappioita | 4,228 % | 4,171 % | 0,057 % |
| Vähemmän molempia rintakuvia | 4,228 % | 4,172 % | 0,055 % |
| Pelaaja voittaa vähemmän aloituksia | -1,914% | -2,039% | 0,125 % |
| Jakaja voittaa lisää aloituksia | -9,121 % | -9,306% | 0,185 % |
| Kokonais | 3,703 % | 3,270 % | 0,433 % |
Samaa taulukkoa on yksinkertaistettu havainnollistamaan suuremman voiton etua, koska jakaja putoaa useammin ja häviää enemmän aloituksia:
Yhteenveto mahdollisista tuloksista, kun pelaaja jää vaikeusasteille 12–16
| Tapahtuma | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Pelaajan pudottamisesta on vähemmän hyötyä | 14,738 % | 14,615 % | 0,123 % |
| Aloitushäviö | -11,035 % | -11,345% | 0,310 % |
| Kokonais | 3,703 % | 3,270 % | 0,433 % |
Yksinkertaisesti sanottuna yhden pakan pelissä pelaaja häviää 14,738 % harvemmin kuin jakaja noudattamalla perusstrategiaa, jossa on vaikea yhteissumma 12–16. Näissä käsissä jakaja ei kuitenkaan häviä 75 %:ssa tapauksista, mikä johtaa jakajan voittoon aloitustilanteessa, jossa pelaajan käsi on 16 tai vähemmän eikä voi voittaa. Kaikkiin käsiin verrattuna pelaaja säästää 14,738 % häviämällä vähemmän, mutta antaa takaisin 11,035 % useampien aloitushäviöiden muodossa, jolloin nettovoitto on 3,703 % yhden pakan pelissä.
Tämä hyöty on vain 3,270 % kahdeksan pakan pelissä. Kaikki asiat huomioon ottaen strategisen aseman hyöty luvuilla 12–16 on pelaajalle 0,433 % arvokkaampi yhden pakan pelissä kuin kahdeksan pakan pelissä.
Miksi strateginen asema on arvokkaampi yhden pakan pelissä kuin kahdeksan pakan pelissä? Vastaus on samanlainen kuin kysymykseen, miksi jakajan asemaetu on merkittävämpi yhden pakan pelissä. Yhden pakan pelissä tapahtuu enemmän korttien menetystä. Vaikka useamman kortin meneminen voi vahingoittaa molempia osapuolia, se haittaa pelaajaa enemmän, koska hän häviää, kun molemmat osapuolet menevät. Nämä kokonaissummat 12–16, kun pelaaja jää, koostuvat todennäköisesti useammasta pienestä kortista kuin suuresta. Tämä jättää pakkaan enemmän korkeita kortteja, jotka voivat mahdollisesti viedä pelaajan. Näiden pelaajan käden parantamiseksi tarvitsemien matalien korttien poistamisen vaikutukset ovat kalliimpia yhden pakan pelissä kuin kahdeksan pakan pelissä. Toisin sanoen, jäykkien korttien osuminen on vaarallisempaa yhden pakan pelissä. Sen sijaan seisominen on hyödyllisempää yhden pakan pelissä.
Tässä on päivitetty taulukko kunkin sääntömuutoksen kustannuksista/hyödyistä:
Sääntöjen vaikutus
| Sääntö | Yhden kannen etu |
|---|---|
| Jälleenmyyjän asemaetu | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | 0,061 % |
| Pelaaja voi jäädä vaikeusasteille 12–16 | 0,433 % |
| Kokonais | 0,415 % |
Pelaaja voi tuplata
Seuraavaksi analysoidaan, mitä hyötyä pelaajalle on tuplaamisen sallimisesta. Vaikutuksen tutkimiseksi pyysin simulaatiota noudattamaan sopivaa tuplausstrategiaa annetulle pakkojen määrälle, joka esitellään myöhemmin artikkelissa. Tämän strategian lisääminen simulaatioon johtaa seuraaviin pelaajan odotettuihin tuottoihin:
- Yksi pakka = -0,556%
- Kahdeksan pakkaa = -1,245 %
Tämä simulaatiotulostaulukko sisältää rivin tämän säännön lisäämistä varten:
Säännön muutoksen odotusarvot
| Sääntö | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Jälleenmyyjän asemaetu | -8,237 % | -8,157% | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | -5,912 % | -5,894% | -0,018% |
| Pelaaja voi jäädä vaikeusasteille 12–16 | -2,209% | -2,625% | 0,415 % |
| Pelaaja voi tuplata | -0,556% | -1,245% | 0,689 % |
Kolmannen ja neljännen rivin välinen ero osoittaa pelaajan vapaan tahdon vaikutuksen tuplaamiseen seuraavasti:
- Yksi pakka = 1,653 %
- Kahdeksan pakkaa = 1,380 %
- Ero = 0,273 %
Näiden kahden luvun erotus osoittaa, että tämän sääntömuutoksen vaikutus on pelaajalle 0,273 % arvokkaampi yhden pakan pelissä verrattuna kahdeksan pakan peliin. Tämä selittää toisen merkittävän osan siitä, miksi yhden pakan peli on pelaajalle 0,563 % arvokkaampi kuin kahdeksan pakan peli.
Miksi tuplaaminen on arvokkaampaa yhden pakan pelissä? Useimmiten pelaaja tuplaa, kun hän tekee tuplauksen, se tapahtuu kovalla 9–11 pisteen yhteissummalla. Tuplaus tehdään kahdella kortilla, joten tarvitaan kaksi keskimääräistä pienempää korttia, jotta yhteissummaksi tulee 9–11. Jos yhdestä korttipakasta poistetaan kaksi pientä korttia, seuraavan kortin todennäköisyys olla kymppi on 32,00 %, mikä on ilmeisen hyvä, kun tuplataan kovalla 9–11 pisteen yhteissummalla. Jos taas kahdeksan pakan kengästä poistetaan kaksi pientä korttia, poistamisen vaikutus ei ole yhtä voimakas, ja seuraavan kortin todennäköisyys olla kymppi on 30,92 %.
Tässä on päivitetty taulukko kunkin sääntömuutoksen kustannuksista/hyödyistä. Huomaa, että kokonaishyöty 0,689 % ylittää lopullisen talon edun eron. Tämä johtuu siitä, että emme ole vielä ottaneet huomioon jakamisen vaikutusta.
Sääntöjen vaikutus
| Sääntö | Yhden kannen etu |
|---|---|
| Jälleenmyyjän asemaetu | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | 0,061 % |
| Pelaaja voi jäädä vaikeusasteille 12–16 | 0,433 % |
| Pelaaja voi tuplata | 0,273 % |
| Kokonais | 0,689 % |
Pelaaja voi jakaa
Seuraavaksi analysoin pelaajan hyötyjä siitä, että hänellä on mahdollisuus jakaa kortteja. Tutkiakseni vaikutusta pyysin simulaattoria noudattamaan sopivaa jakostrategiaa annetulle pakkojen määrälle, joka esitellään myöhemmin artikkelissa. Tämän strategian lisääminen johtaa meidät täyteen perusstrategiaan. Pelaajan ja jakajan välillä ei ole muita sääntöeroja, joita olisi tutkittava jakamisen lisäämisen jälkeen. Täydellisen perusstrategian pelaajan odotetut tuotot ovat:
- Yksi pakka = -0,012 %
- Kahdeksan pakkaa = -0,575 %
Simulaatiotulostaulukko, joka sisältää rivin tämän säännön lisäämistä varten, on seuraava:
Säännön muutoksen odotusarvot
| Sääntö | Yksi kansi | Kahdeksan pakkaa | Ero |
|---|---|---|---|
| Jälleenmyyjän asemaetu | -8,237 % | -8,157% | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | -5,912 % | -5,894% | -0,018% |
| Pelaaja voi jäädä vaikeusasteille 12–16 | -2,209% | -2,625% | 0,415 % |
| Pelaaja voi tuplata | -0,556% | -1,245% | 0,689 % |
| Pelaaja voi jakaa | -0,012 % | -0,575% | 0,563 % |
Neljännen ja viidennen rivin ero osoittaa pelaajan vapaan tahdon vaikutuksen jakaa.
- Yksi pakka = 0,544 %
- Kahdeksan pakkaa = 0,669 %
- Ero = -0,125 %
Näiden kahden luvun erotus osoittaa, että tämän sääntömuutoksen vaikutus on pelaajalle 0,125 % pienempi yhden pakan pelissä verrattuna kahdeksan pakkaa käyttävään peliin.
Syy siihen, miksi jakaminen on hyödyllisempää kahdeksan pakan pelissä yhden pakan peliin verrattuna, on se, että kahden ensimmäisen kortin parin saamisen todennäköisyys on suurempi. Tarkemmin sanottuna kahdeksalla pakalla, Excelin terminologiaa käyttäen, todennäköisyys on 13*combin(4*8,2)/combin(52*8,2) = 7,470 %. Yhdellä pakalla todennäköisyys on 13*combin(4*1,2)/combin(52*1,2) = 5,882 %.
Muista myös, että peruspelin säännöt sallivat uudelleenjakamisen jopa kolme kertaa tai neljään käteen. Jos yhdestä pakasta poistetaan kaksi samanarvoista korttia, todennäköisyys saada sama arvo seuraavalla kortilla on 2/50 = 4,000 %. Kahdeksan pakan korttipakassa tämä todennäköisyys on 30/414 = 7,246 %. Koska yhden pakan pelissä jakamista ja uudelleenjakamista tapahtuu vähemmän, jakamisen kokonaisarvo on pienempi. Tämä selittää, miksi jakamisen hyöty pienenee siirryttäessä kahdeksasta yhteen pakkaan.
Yhden pakan peliin jakamisen negatiivisen vaikutuksen lisääminen täydentää taulukkomme, jossa tarkastellaan eri sääntöjen vaikutusta yhden pakan pelin hyötyihin kahdeksaan pakkaan verrattuna.
Sääntö Yhden pakan hyöty Jakajan asemaetu -0,079 % Voittavan pelaajan blackjack maksaa 3–2 0,061 % Pelaaja voi jäädä, jos korttien määrä on 12–16 0,433 % Pelaaja voi tuplata 0,273 % Pelaaja voi jakaa -0,125 % Yhteensä 0,563 %Huomaa, että oikean alakulman solun summa 0,563 % vastaa artikkelin alussa mainitun talon etulaskimen antamia eroja. Tässä on sama taulukko vaikutusjärjestyksessä:
Sääntöjen vaikutus
| Sääntö | Yhden kannen etu |
|---|---|
| Jälleenmyyjän asemaetu | -0,079% |
| Voittavan pelaajan blackjack maksaa 3:2 | 0,061 % |
| Pelaaja voi jäädä vaikeusasteille 12–16 | 0,433 % |
| Pelaaja voi tuplata | 0,273 % |
| Pelaaja voi jakaa | -0,125 % |
| Kokonais | 0,563 % |
Perusstrategiataulukot
Seuraava taulukko näyttää sopivan perusstrategian annetuille säännöille ja yhdelle pakalle.
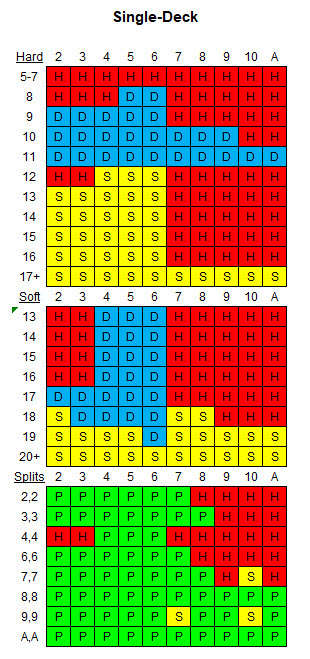
Seuraava taulukko näyttää sopivan perusstrategian annetuille säännöille ja kahdeksalle pakalle.

Odotusarvotaulukot
Seuraava taulukko näyttää kunkin aloituskäden odotusarvon yhden pakan pelissä. Ylimmällä rivillä näkyy jakajan kuvapuoli ylöspäin oleva kortti. Odotusarvot mitataan ennen kuin jakaja tarkistaa blackjackin. Yhteensä-sarake näyttää kunkin rivin odotusarvojen painotetun keskiarvon käden saamisen todennäköisyyden mukaan. Oikeassa alakulmassa näkyy koko pelin odotusarvo.
Odotusarvot yhden pakan pelissä
Odotusarvot pelaajan käden ja jakajan näkyvän kortin välillä, jossa on yksi paka
| Pelaaja | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ässä | Kokonais |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,1278 | -0,0968 | -0,0379 | 0,0227 | 0,0403 | -0,1191 | -0,1805 | -0,2624 | -0,3654 | -0,5443 | -0,2169 |
| 6 | -0,1477 | -0,1037 | -0,0519 | 0,0104 | 0,0371 | -0,1640 | -0,2343 | -0,3046 | -0,4015 | -0,5713 | -0,2469 |
| 7 | -0,1120 | -0,0701 | -0,0119 | 0,0528 | 0,0683 | -0,0690 | -0,2232 | -0,2948 | -0,3863 | -0,5765 | -0,2211 |
| 8 | -0,0174 | 0,0199 | 0,0826 | 0,1407 | 0,1498 | 0,0921 | -0,0565 | -0,2135 | -0,3136 | -0,5144 | -0,1286 |
| 9 | 0,1124 | 0,1923 | 0,2837 | 0,3753 | 0,3799 | 0,1951 | 0.1111 | -0,0519 | -0,2165 | -0,4146 | 0,0151 |
| 10 | 0,4262 | 0,4908 | 0,5494 | 0,6276 | 0,6241 | 0,4458 | 0,3145 | 0,1644 | -0,0528 | -0,2991 | 0,2316 |
| 11 | 0,5428 | 0,5922 | 0,6516 | 0,7176 | 0,7198 | 0,4785 | 0,3417 | 0,2240 | 0,0670 | -0,1848 | 0,3268 |
| 12 | -0,2518 | -0,2255 | -0,1915 | -0,1364 | -0,1194 | -0,2273 | -0,2925 | -0,3639 | -0,4175 | -0,5824 | -0,3131 |
| 13 | -0,2879 | -0,2411 | -0,1816 | -0,1344 | -0,1208 | -0,2861 | -0,3461 | -0,3764 | -0,4590 | -0,6106 | -0,3415 |
| 14 | -0,2900 | -0,2391 | -0,1835 | -0,1342 | -0,1209 | -0,3442 | -0,3612 | -0,4192 | -0,4957 | -0,6356 | -0,3644 |
| 15 | -0,2803 | -0,2379 | -0,1837 | -0,1388 | -0,1266 | -0,3590 | -0,4133 | -0,4703 | -0,5397 | -0,6677 | -0.3893 |
| 16 | -0,2863 | -0,2446 | -0,1872 | -0,1435 | -0,1450 | -0,3760 | -0,4254 | -0,4797 | -0,5482 | -0,6739 | -0,3978 |
| 17 | -0,1568 | -0,1216 | -0,0712 | -0,0445 | -0,0306 | -0,1217 | -0,3976 | -0,4154 | -0,4562 | -0,6560 | -0,2947 |
| 18 | 0,1072 | 0,1359 | 0,1538 | 0,1983 | 0,2031 | 0,3887 | 0,0956 | -0,1961 | -0,2242 | -0,4527 | -0,0185 |
| 19 | 0,3763 | 0,3774 | 0,3965 | 0,4449 | 0,4364 | 0,6101 | 0,5769 | 0,2642 | 0,0125 | -0,1586 | 0,2644 |
| A,2 | 0,0402 | 0,0711 | 0,1174 | 0,2130 | 0,2455 | 0,1074 | 0,0392 | -0,0141 | -0,1454 | -0,3991 | -0,0057 |
| A,3 | 0,0184 | 0,0447 | 0,1127 | 0,2042 | 0,2391 | 0,0605 | 0,0349 | -0,0602 | -0,1781 | -0,4205 | -0,0308 |
| A,4 | -0,0103 | 0,0237 | 0,0892 | 0,1753 | 0,2191 | 0,0339 | -0,0354 | -0,1136 | -0,2226 | -0,4533 | -0,0697 |
| A,5 | -0,0298 | -0,0019 | 0,0667 | 0,1490 | 0,2327 | -0,0239 | -0,0842 | -0,1666 | -0,2760 | -0,4900 | -0,1094 |
| A,6 | 0,0142 | 0,0743 | 0,1549 | 0,2805 | 0,2630 | 0,0597 | -0,0646 | -0,1348 | -0,2383 | -0,4810 | -0,0586 |
| A,7 | 0,1279 | 0,1867 | 0,3091 | 0,3482 | 0,3623 | 0,4118 | 0,1209 | -0,0873 | -0,1926 | -0,4433 | 0,0459 |
| A,8 | 0,3953 | 0,4157 | 0,4100 | 0,4593 | 0,4666 | 0,6146 | 0,6078 | 0,2882 | -0,0009 | -0,1938 | 0,2686 |
| A,9 | 0,6525 | 0,6415 | 0,6507 | 0,6810 | 0,6730 | 0,7732 | 0,7848 | 0,7656 | 0,4594 | 0,0943 | 0,5871 |
| A,10 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1.4081 | 1.0409 | 1,4449 |
| A, A | 0,6384 | 0,6863 | 0,7417 | 0,8075 | 0,8289 | 0,6277 | 0,4865 | 0,3605 | 0,2080 | -0,1580 | 0,4744 |
| 2,2 | -0,0349 | 0,0396 | 0,1235 | 0,3014 | 0,3378 | 0,0137 | -0,1412 | -0,2224 | -0,3355 | -0,5246 | -0,1145 |
| 3,3 | -0,1082 | -0,0209 | 0,1607 | 0,3049 | 0,3395 | -0,0448 | -0,2232 | -0,3100 | -0,3986 | -0,5715 | -0,1646 |
| 4,4 | -0,0136 | 0,0268 | 0,1354 | 0,2680 | 0,2980 | 0,1104 | -0,0549 | -0,2063 | -0,3069 | -0,5065 | -0,0991 |
| 5,5 | 0,4441 | 0,5075 | 0,5870 | 0,6933 | 0,7084 | 0,4663 | 0,3227 | 0.1738 | -0,0510 | -0,2978 | 0,2444 |
| 6,6 | -0,0963 | 0,0132 | 0,1456 | 0,2786 | 0,1992 | -0,1933 | -0,3222 | -0,3862 | -0,4366 | -0,5989 | -0,2245 |
| 7,7 | -0,0546 | 0,0494 | 0,1879 | 0,2244 | 0,2396 | -0,0524 | -0,3804 | -0,4744 | -0,5556 | -0,6790 | -0,2508 |
| 8,8 | 0,1165 | 0,1873 | 0,2245 | 0,3287 | 0,3508 | 0,3040 | -0,0599 | -0,4017 | -0,4929 | -0,6389 | -0,1224 |
| 9,9 | 0,2052 | 0,2156 | 0,3070 | 0,4064 | 0,4080 | 0,4011 | 0,2067 | -0,0986 | -0,2041 | -0,4520 | 0,0666 |
| 10,10 | 0,6220 | 0,6323 | 0,6402 | 0,6718 | 0,6683 | 0,7647 | 0,7832 | 0,7440 | 0,4539 | 0,1383 | 0,5803 |
| Kokonais | 0,1021 | 0,1388 | 0,1860 | 0,2391 | 0,2471 | 0,1473 | 0,0551 | -0,0435 | -0,1712 | -0,3891 | -0,0001 |
Odotusarvot kahdeksan pakan pelissä
Odotusarvot pelaajan käden ja jakajan näkyvän kortin välillä, kun pakassa on kahdeksan korttia
| Pelaaja | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ässä | Kokonais |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,1258 | -0,0929 | -0,0562 | -0,0175 | 0,018 | -0,1196 | -0,1871 | -0,266 | -0,3663 | -0,5291 | -0,2191 |
| 6 | -0,1389 | -0,1042 | -0,0677 | -0,0287 | 0,0085 | -0,1534 | -0,2192 | -0,2941 | -0,3902 | -0,5469 | -0,2395 |
| 7 | -0,1094 | -0,0760 | -0,0391 | -0,0004 | 0,0349 | -0,0689 | -0,2121 | -0,2866 | -0,3731 | -0,5526 | -0,2164 |
| 8 | -0,0234 | 0,0076 | 0,0427 | 0,0774 | 0,1079 | 0,0831 | -0,0595 | -0,2104 | -0,3079 | -0,4931 | -0,1316 |
| 9 | 0,0743 | 0,1277 | 0,1921 | 0,2580 | 0,3141 | 0,1745 | 0,0998 | -0,0522 | -0,2180 | -0,3962 | -0,0071 |
| 10 | 0,3653 | 0,4176 | 0,4704 | 0,5253 | 0,5723 | 0,3990 | 0,2895 | 0,1469 | -0,0535 | -0,2865 | 0,2056 |
| 11 | 0,4786 | 0,5264 | 0,5759 | 0,6271 | 0,6718 | 0,4653 | 0,3496 | 0,2271 | 0,0864 | -0,2297 | 0,3097 |
| 12 | -0,2535 | -0,2331 | -0,2041 | -0,1613 | -0,1208 | -0,2146 | -0,2741 | -0,3430 | -0,4273 | -0,5746 | -0,3146 |
| 13 | -0,2867 | -0,2461 | -0,2030 | -0,1611 | -0,1210 | -0,2713 | -0,3264 | -0,3858 | -0,4682 | -0,6049 | -0,3447 |
| 14 | -0,2870 | -0,2456 | -0,2034 | -0,1612 | -0,1211 | -0,3240 | -0,3707 | -0,4295 | -0,5059 | -0,6328 | -0,3694 |
| 15 | -0,2858 | -0,2456 | -0,2033 | -0,1616 | -0,1217 | -0,3683 | -0,4162 | -0,4715 | -0,5422 | -0,6597 | -0,3927 |
| 16 | -0,2866 | -0,2463 | -0,2038 | -0,1622 | -0,1236 | -0,4103 | -0,4547 | -0,5057 | -0,5721 | -0,6820 | -0,4128 |
| 17 | -0,1565 | -0,1205 | -0,0819 | -0,0461 | -0,0090 | -0,1085 | -0,3842 | -0,4223 | -0,4633 | -0,6636 | -0,2958 |
| 18 | 0,1098 | 0,1379 | 0,1648 | 0,1953 | 0,2211 | 0,3982 | 0,1045 | -0,1847 | -0,2394 | -0,4626 | -0,0208 |
| 19 | 0,3780 | 0,3949 | 0,4138 | 0.4372 | 0,4513 | 0,6153 | 0,5918 | 0,2848 | -0,0149 | -0,1753 | 0,2569 |
| A,2 | 0,0458 | 0,0737 | 0,1041 | 0,1376 | 0,2024 | 0,1207 | 0,0523 | -0,0350 | -0,1703 | -0,3789 | -0,0269 |
| A,3 | 0,0224 | 0,0507 | 0,0827 | 0,1366 | 0.2010 | 0,0769 | 0,0155 | -0,0733 | -0,2024 | -0,4031 | -0,0533 |
| A,4 | -0,0006 | 0,0294 | 0,0641 | 0,1328 | 0,1986 | 0,0368 | -0,0282 | -0,1123 | -0,2357 | -0,4281 | -0,0803 |
| A,5 | -0,0211 | 0,0088 | 0,0611 | 0,1301 | 0,2004 | -0,0070 | -0,0689 | -0,1507 | -0,2691 | -0,4532 | -0,1057 |
| A,6 | -0,0006 | 0,0558 | 0,1220 | 0,1933 | 0,2513 | 0,0545 | -0,0721 | -0,1479 | -0,2563 | -0,4626 | -0,0792 |
| A,7 | 0,1160 | 0,1749 | 0,2418 | 0,3000 | 0,3560 | 0,4014 | 0,1074 | -0,0990 | -0,2075 | -0,4205 | 0,0270 |
| A,8 | 0,3800 | 0,3993 | 0,4157 | 0,4389 | 0,4621 | 0,6159 | 0,5953 | 0,2878 | -0,0164 | -0,1795 | 0,2579 |
| A,9 | 0,6371 | 0,6455 | 0,6562 | 0,6699 | 0,6778 | 0,7732 | 0,7909 | 0,7591 | 0,4379 | 0,1070 | 0,5752 |
| A,10 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1,5000 | 1.3874 | 1.0388 | 1,4309 |
| A, A | 0,6072 | 0,6561 | 0,7062 | 0,7588 | 0,8058 | 0,6277 | 0,5001 | 0,3629 | 0,2059 | -0,1511 | 0,4411 |
| 2,2 | -0,0797 | -0,0089 | 0,0697 | 0,1700 | 0,2643 | 0,0087 | -0,1576 | -0,2385 | -0,3430 | -0,5115 | -0,1430 |
| 3,3 | -0,1305 | -0,0482 | 0,0500 | 0,1502 | 0,2425 | -0,0518 | -0,2189 | -0,2946 | -0,3899 | -0,5465 | -0,1859 |
| 4,4 | -0,0225 | 0,0080 | 0,0441 | 0,1066 | 0,2027 | 0,0857 | -0,0595 | -0,2096 | -0,3070 | -0,4921 | -0,1212 |
| 5,5 | 0,3676 | 0,4201 | 0,4748 | 0,5324 | 0,5814 | 0,4012 | 0,2910 | 0,1477 | -0,0534 | -0,2863 | 0,2074 |
| 6,6 | -0,1947 | -0,0972 | 0,0043 | 0,1075 | 0,1900 | -0,2189 | -0,2775 | -0,3453 | -0,4295 | -0,5767 | -0,2426 |
| 7,7 | -0,1233 | -0,0335 | 0,0669 | 0,1569 | 0,2508 | -0,0485 | -0,3765 | -0,4361 | -0,5129 | -0,6382 | -0,2497 |
| 8,8 | 0,0720 | 0,1452 | 0,2171 | 0,3005 | 0,3753 | 0,3195 | -0,0276 | -0,3893 | -0,5170 | -0,6660 | -0,1329 |
| 9,9 | 0.1943 | 0,2506 | 0,3196 | 0,3925 | 0,4551 | 0,3996 | 0,2308 | -0,0801 | -0,2369 | -0,4624 | 0,0585 |
| 10,10 | 0,6334 | 0,6442 | 0,6549 | 0,6688 | 0,6770 | 0,7723 | 0,7907 | 0,7566 | 0,4373 | 0,1124 | 0,5745 |
| Kokonais | 0,0927 | 0,1262 | 0,1628 | 0,2025 | 0,2390 | 0,1453 | 0,0585 | -0,0403 | -0,1727 | -0,3712 | -0,0058 |
Odotusarvon erot (%)
Seuraava taulukko näyttää odotusarvon yhden pakan pelissä vähennettynä kahdeksan pakan pelillä prosentuaalisesti.
Odotusarvojen muutos pelaajan käden ja jakajan näkyvän kortin mukaan (x100)
| Pelaaja | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Ässä | Kokonais |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -0,196 | -0,383 | 1.834 | 4.02 | 2.229 | 0,05 | 0,664 | 0,361 | 0,087 | -1,52 | 0,22 |
| 6 | -0,8770 | 0,0480 | 1.5840 | 3.9030 | 2.8630 | -1,0640 | -1,5170 | -1,0490 | -1,1320 | -2,4330 | -0,7380 |
| 7 | -0,2560 | 0,5920 | 2.7210 | 5.3240 | 3.3400 | -0,0070 | -1,1090 | -0,8160 | -1,3150 | -2,3840 | -0,4720 |
| 8 | 0,6060 | 1.2300 | 3.9870 | 6.3300 | 4.1900 | 0,9040 | 0,3020 | -0,3070 | -0,5740 | -2,1370 | 0,2910 |
| 9 | 3.8080 | 6.4600 | 9.1610 | 11.7320 | 6.5770 | 2.0670 | 1.1320 | 0,0300 | 0,1480 | -1,8380 | 2.2220 |
| 10 | 6.0970 | 7.3170 | 7.8980 | 10.2270 | 5.1830 | 4.6820 | 2.4980 | 1,7530 | 0,0720 | -1,2510 | 2.6040 |
| 11 | 6.4200 | 6.5830 | 7.5650 | 9.0560 | 4.8030 | 1.3220 | -0,7900 | -0,3170 | -1,9460 | 4.4940 | 1.7050 |
| 12 | 0,1670 | 0,7540 | 1.2640 | 2.4890 | 0,1350 | -1,2760 | -1,8390 | -2,0880 | 0,9840 | -0,7830 | 0,1460 |
| 13 | -0,1260 | 0,5070 | 2.1460 | 2.6670 | 0,0210 | -1,4780 | -1,9700 | 0,9410 | 0,9190 | -0,5660 | 0,3180 |
| 14 | -0,2970 | 0,6510 | 1.9930 | 2.6980 | 0,0150 | -2,0210 | 0,9460 | 1.0330 | 1.0240 | -0,2860 | 0,5000 |
| 15 | 0,5560 | 0,7690 | 1,9570 | 2.2820 | -0,4950 | 0,9270 | 0,2900 | 0,1190 | 0,2470 | -0,7990 | 0,3400 |
| 16 | 0,0300 | 0,1700 | 1,6680 | 1,8640 | -2,1330 | 3.4380 | 2.9220 | 2.6000 | 2.3870 | 0,8060 | 1,4950 |
| 17 | -0,0300 | -0,1100 | 1.0720 | 0,1630 | -2,1630 | -1,3190 | -1,3380 | 0,6910 | 0,7130 | 0,7580 | 0,1060 |
| 18 | -0,2560 | -0,2000 | -1,0990 | 0,2950 | -1,7950 | -0,9490 | -0,8890 | -1,1420 | 1.5210 | 0,9900 | 0,2340 |
| 19 | -0.1730 | -1,7470 | -1,7360 | 0,7660 | -1,4910 | -0,5200 | -1,4980 | -2,0590 | 2.7370 | 1,6770 | 0,7460 |
| A,2 | -0,5660 | -0,2590 | 1.3280 | 7.5340 | 4.3080 | -1,3290 | -1,3120 | 2.0900 | 2.4910 | -2,0210 | 2.1220 |
| A,3 | -0,4090 | -0,6000 | 3.0040 | 6.7580 | 3.8040 | -1,6410 | 1.9440 | 1.3040 | 2.4300 | -1,7440 | 2.2470 |
| A,4 | -0,9750 | -0,5720 | 2.5100 | 4.2580 | 2.0490 | -0,2980 | -0,7230 | -0,1290 | 1.3080 | -2,5210 | 1.0610 |
| A,5 | -0,8730 | -1,0720 | 0,5650 | 1,8950 | 3.2330 | -1,6930 | -1,5280 | -1,5890 | -0,6930 | -3,6740 | -0,3690 |
| A,6 | 1,4820 | 1.8480 | 3.2870 | 8.7240 | 1.1650 | 0,5180 | 0,7480 | 1.3090 | 1,7920 | -1,8340 | 2.0600 |
| A,7 | 1.1920 | 1.1830 | 6.7250 | 4.8180 | 0,6310 | 1.0410 | 1.3420 | 1.1640 | 1,4890 | -2,2860 | 1.8940 |
| A,8 | 1,5370 | 1,6390 | -0,5690 | 2.0370 | 0,4540 | -0,1320 | 1.2540 | 0,0390 | 1,5550 | -1,4310 | 1.0640 |
| A,9 | 1,5370 | -0,3990 | -0,5560 | 1.1160 | -0,4780 | 0,0020 | -0,6060 | 0,6480 | 2.1530 | -1,2700 | 1.1970 |
| A,10 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 2.0730 | 0,2070 | 1.3970 |
| A, A | 3.1200 | 3.0230 | 3.5450 | 4.8720 | 2.3070 | 0.0000 | -1,3620 | -0,2430 | 0,2140 | -0,6920 | 3.3340 |
| 2,2 | 4.4790 | 4.8510 | 5.3790 | 13.1380 | 7.3480 | 0,4980 | 1,6370 | 1,6100 | 0,7540 | -1,3140 | 2.8470 |
| 3,3 | 2.2320 | 2.7290 | 11.0750 | 15.4710 | 9.7010 | 0,7020 | -0,4300 | -1,5380 | -0,8700 | -2,4920 | 2.1250 |
| 4,4 | 0,8840 | 1,8800 | 9.1320 | 16.1400 | 9.5290 | 2.4760 | 0,4550 | 0,3380 | 0,0090 | -1,4460 | 2.2100 |
| 5,5 | 7.6550 | 8.7410 | 11.2230 | 16.0940 | 12.6990 | 6.5150 | 3.1720 | 2.6130 | 0,2380 | -1,1510 | 3.7020 |
| 6,6 | 9.8410 | 11.0360 | 14.1250 | 17.1060 | 0,9170 | 2.5610 | -4,4720 | -4,0910 | -0,7110 | -2,2180 | 1.8060 |
| 7,7 | 6.8730 | 8.2850 | 12.1030 | 6.7540 | -1,1240 | -0,3840 | -0,3830 | -3,8370 | -4,2660 | -4,0800 | -0,1170 |
| 8,8 | 4.4530 | 4.2080 | 0,7370 | 2.8160 | -2,4470 | -1,5490 | -3,2240 | -1,2460 | 2.4110 | 2.7050 | 1.05.00 |
| 9,9 | 1.0910 | -3,5070 | -1,2560 | 1.3820 | -4,7120 | 0,1480 | -2,4060 | -1,8530 | 3.2860 | 1.0450 | 0,8060 |
| 10,10 | -1,1490 | -1.1970 | -1,4750 | 0,2960 | -0,8740 | -0,7630 | -0,7510 | -1,2620 | 1,6580 | 2.5910 | 0,5780 |
| Kokonais | 0,9370 | 1.2510 | 2.3110 | 3.6590 | 0,8050 | 0,1970 | -0,3390 | -0,3210 | 0,1480 | -1,7900 | 0,5620 |
Lisälukemista
Peter Griffinin teos ”The Theory of Blackjack” käsittelee aihetta parhaiten, mitä olen nähnyt. Hän käsittelee aihetta luvussa 8, jonka otsikko on ”Monia pakkoja ja erilaisia sääntöjä”, jossa käytetään erilaisia perussääntöjä ja lasketaan yhden pakan ja äärettömän monen pakan välinen ero. Hän ei aina anna tarkkoja lukuja kaikelle, vaan mukailee 0,69 %:n eron jakautumista oletustensa mukaisesti seuraavasti:
- Tuplaaminen: Lähes puolet 0,69 prosentista
- Pelaajan blackjackit: 0,07 %
- Splittaus: Se kumoaa blackjackin hyödyt enemmän kuin
- Seisomassa kohtien 12 ja 16 kohdalla: ”Oletettavasti jäljellä oleva ristiriita.”
Griffin jatkaa luettelemalla erilaisten sääntömuutosten etuja sekä yhden pakan että äärettömien pakan alla.
Kiitokset
Haluan kiittää Don Schlesingeriä hänen viisaista neuvoistaan tämän artikkelin analysoinnissa ja oikoluvussa.


