Tällä sivulla
Bonus-craps
Johdanto
Bonus Craps on kolmen craps-pelissä esiintyvän sivupanoksen sarja. Ne ovat seuraavat:
- Pieni – Voittaa, jos heittäjä heittää jokaisen yhteistuloksen 2:sta 6:een ennen kuin saa kokonaistuloksen 7. Voitot maksetaan yleensä suhteessa 30:1.
- Korkea – Voittaa, jos heittäjä heittää jokaisen yhteistuloksen 8:sta 12:een ennen kuin heittää yhteensä 7. Voitot maksetaan yleensä suhteessa 30:1.
- Kaikki – Voitto, jos heittäjä heittää kaikki yhteistulokset 2:sta 12:een, paitsi 7, ennen kuin heittää yhteensä 7. Voitot maksetaan yleensä suhteessa 150:1.
Vuonna 2021 aloin nähdä samoja "Diceology"-nimisiä vetoja Venetianissa.
Analyysi
Seuraava taulukko näyttää analyysini pienistä ja suurista panoksista, joissa voitot maksavat takaisin kertoimella 30:1. Oikeassa alakulmassa näkyy 18,30 %:n talon etu.
Pieni ja pitkä
| Tapahtuma | Maksaa | Todennäköisyys | Palata |
|---|---|---|---|
| Voittaa | 30 | 0,026354 | 0,790617 |
| Menetys | -1 | 0,973646 | -0,973646 |
| Kokonais | 1.000000 | -0,183029 |
Aikaisemmin joidenkin pöytien tiedettiin maksavan 34:1-kertoimella Small and Tall -pöydissä. Näissä anteliaammissa kertoimissa talon etu on 7,76 %.
Seuraava taulukko näyttää analyysini All-betistä, jossa voitot maksavat takaisin kertoimella 150:1. Oikeassa alakulmassa näkyy talon etu 20,61 %.
Kaikki
| Tapahtuma | Maksaa | Todennäköisyys | Palata |
|---|---|---|---|
| Voittaa | 150 | 0,005258 | 0,788655 |
| Menetys | -1 | 0,994742 | -0,994742 |
| Kokonais | 1.000000 | -0,206087 |
Olen nähnyt muita voittoja All-vedossa, mukaan lukien 155 ja 175:1. Muista vähentää yksi voitosta muuntaaksesi kertoimet "yhdelle" kertoimeksi "yhdelle". Seuraava taulukko näyttää talon edun kaikille viidellä jaollisille voittokertoimille väliltä 150:175.
Talon edun yhteenveto All Bet -sivustolla
| Maksaa | Talon etu |
|---|---|
| 150 | 20,61 % |
| 155 | 17,98 % |
| 160 | 15,35 % |
| 165 | 12,72 % |
| 170 | 10,09 % |
| 175 | 7,46 % |
Metodologia
Olen analysoinut Bonus Crapsia kolmella tavalla seuraavasti:
- Simulointi — Tämä on luultavasti helpoin tapa. Matemaattisille puristeille, kuten minulle, simulaatiot ovat kuitenkin aina älyllisesti tyydyttämättömiä.
- Markov-ketju — Tämä menetelmä on työläs ja aikaa vievä. Pienelle ja pitkälle se vaatisi 6x6-siirtymämatriisin ja Kaikille 12x12-siirtymämatriisin.
- Integraalilaskenta — Tämä menetelmä on yllättävän helppo integraalilaskimen avulla. Selitän sen tarkemmin alla.
Kuvittele, että merkittävien tapahtumien yksi kerrallaan määrittämisen sijaan nopanheitto voi tarkoittaa yksittäistä hetkeä. Oletetaan, että tapahtumien välinen aika ei säilytä muistia ja että tapahtumien välinen keskimääräinen aika on yksi aikayksikkö. Toisin sanoen tapahtumien välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 1. Tällä ei ole merkitystä vedon ratkaisemisen kannalta, koska tapahtumat tapahtuvat edelleen yksi kerrallaan.
Seuraava on todennäköisyys sille, että mitä tahansa kokonaislukua EI ole heitetty ainakin kerran x aikayksikön sisällä:
- 2 tai 12: exp(-x/36)
- 3 tai 11: exp(-x/18)
- 4 tai 10: exp(-x/12)
- 5 tai 9: exp(-x/9)
- 6 tai 8: kokemus(-5x/36)
- 7: exp(-x/6)
Tarkastellaan ensin pientä panosta. Kertoimet ovat täsmälleen samat ison panoksen kohdalla.
X aikayksikössä todennäköisyys sille, että luvut 2, 3, 4, 5 ja 6 on heitetty, mutta 7 ei, on: (1-op(-x/36))*(1-op(-x/18))*(1-op(-x/12))*(1-op(-x/9))*(1-op(-5x/36))*op(-x/6). Todennäköisyys sille, että hetkellä x pelaaja heittää luvun 7 heitettyään aiemmin kaikki yhteistulokset 2:sta 6:een, on:
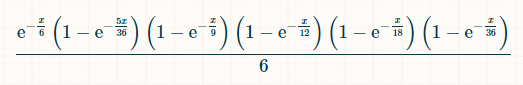
Integrointiin käytin tätä integraalilaskuria .
Koska voittava 7 voi tapahtua milloin tahansa, voittotodennäköisyys on tämän todennäköisyyden integraali x:n yli nollasta äärettömyyteen. Ei sillä, että meidän tarvitsisi tietää, mutta integraali on ennen integroinnin rajojen asettamista (-6*e^(-x/6)+(36*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-(36*e^(-(11*x)/36))/11-3*e^(-x/3)-(36*e^(-(13*x)/36))/13+(18*e^(-(7*x)/18))/7+(12*e^(-(5*x)/12))/5+(9*e^(-(4*x)/9))/4-(36*e^(-(19*x)/36))/19-(9*e^(-(5*x)/9))/5+(12*e^(-(7*x)/12))/7)/6.
Integroinnin rajat huomioon ottaen vastaus on 20049 / 760760 = approksim. 0,02635390924864609.
Seuraavaksi tarkastellaan All-betiä.
X aikayksikössä todennäköisyys sille, että luvut 2, 3, 4, 5, 6, 8, 9, 10, 11 ja 12 on heitetty, mutta 7 ei, on: (1-op(-x/36)) 2 *(1-op(-x/16)) 2 *(1-op(-x/12)) 2 *(1-op(-x/9)) 2 *(1-op(-5x/36)) 2 *op(-x/6). Todennäköisyys sille, että hetkellä x pelaaja heittää 7 heitettyään ensin kaikki yhteistulokset 2:sta 6:een, on:
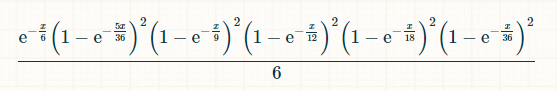
Koska voittava 7 voi tapahtua milloin tahansa, voittotodennäköisyys on tämän todennäköisyyden integraali x:n yli nollasta äärettömyyteen. Ei sillä, että meidän tarvitsisi tietää, mutta integraali on, ennen integroinnin rajojen asettamista, (-6*e^(-x/6)+(72*e^(-(7*x)/36))/7+(9*e^(-(2*x)/9))/2-8*e^(-x/4)-(18*e^(-(5*x)/18))/5-(72*e^(-(11*x)/36))/11+(72*e^(-(13*x)/36))/13+(108*e^(-(7*x)/1 8))/7+(24*e^(-(5*x)/12))/5-(27*e^(-(4*x)/9))/4-(216*e^(-(17*x)/36))/17-10* e^(-x/2)-(72*e^(-(19*x)/36))/19+(27*e^(-(5*x)/9))/5+(144*e^(-(7*x)/12))/7+ (54*e^(-(11*x)/18))/11-(72*e^(-(23*x)/36))/23-(15*e^(-(2*x)/3))/2-(216*e^( -(25*x)/36))/25-(54*e^(-(13*x)/18))/13+(8*e^(-(3*x)/4))/3+(54*e^(-(7*x)/9) )/7+(72*e^(-(29*x)/36))/29-(72*e^(-(31*x)/36))/31-(9*e^(-(8*x)/9))/8-(24*e) ^(-(11*x)/12))/11+(18*e^(-(17*x)/18))/17+(72*e^(-(35*x)/36))/35-e^(-x))/6.
Integroinnin rajat huomioon ottaen vastaus on 126538525259 / 24067258815600 = 0,0052577040961964420049.



