Tällä sivulla
Erilaiset tuplaukset
Johdanto
Different Doubles on craps-sivupanos, jota on nähty Beau Rivage -kasinolla Biloxissa. Se maksaa voittoja heittäjän heittämien ainutlaatuisten tuplausten lukumäärän perusteella ennen kuin heittää yhteensä seitsemän. Voittotaulukko on seuraava:
- 6 tuplaa maksaa 100:1
- 5 tuplaa voittaa kertoimella 15:1
- 4 tuplaa maksaa 8:1
- 3 tuplaa maksaa 4:1
Analyysi
Alla oleva taulukko näyttää kaikkien mahdollisten tulosten todennäköisyyden ja vaikutuksen palautukseen. Oikeassa alakulmassa näkyy talon etu 27,92 % (ai!).
Eri nelinpelien palautustaulukko
| Tuplaa tehty | Maksaa | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|---|
| 6 | 100 | 1 | 0,001082 | 0.108225 |
| 5 | 15 | 6 | 0,006494 | 0,097403 |
| 4 | 8 | 21 | 0,022727 | 0.181818 |
| 3 | 4 | 56 | 0,060606 | 0.242424 |
| 2 | -1 | 126 | 0,136364 | -0,136364 |
| 1 | -1 | 252 | 0,272727 | -0,272727 |
| 0 | -1 | 462 | 0,500000 | -0,500000 |
| Kokonais | 924 | 1.000000 | -0,279221 |
Algebrallinen analyysi
Minkä tahansa tuplan todennäköisyys on 1/36. Näin ollen MINKÄ TAHANSA tuplan todennäköisyys on 6/36 = 1/6. Minkä tahansa seiskan todennäköisyys on 1/6. Voimme jättää huomiotta kaikki muut heitot paitsi tuplat ja seiskat. Olettaen siis, että vedossa oli olennainen heitto, alla ovat kyseisen heiton todennäköisyydet:
- Mikä tahansa tupla = 1/2
- Mikä tahansa seitsemän = 1/2
Todennäköisyys sille, että ensimmäinen merkittävä heitto on seiska, on 1/2. Näin ollen tuplausten todennäköisyys on nolla.
Muuten pelaaja olisi heittänyt tuplan. Voimme nyt jättää tuplan heittämisen uudelleen huomiotta merkittävänä tapahtumana. Molempien merkittävien tapahtumien tyyppien todennäköisyydet ovat nyt:
- Mikä tahansa merkittävä tupla = 5/11
- Mikä tahansa seitsemän = 6/11
Todennäköisyys sille, että pelaaja heittää tässä vaiheessa seiskan, eli yhden tuplan, on 6/11. Näin ollen yhden tuplan kokonaistodennäköisyys on (1/2) * (6/11) = 3/11 = noin 27,27 %.
Muuten pelaaja olisi heittänyt toisen tuplan. Voimme nyt jättää kaksi erillistä tuplaa huomiotta merkittävänä tapahtumana. Molempien merkittävien tapahtumien todennäköisyydet ovat nyt:
- Mikä tahansa merkittävä tupla = 4/10
- Mikä tahansa seitsemän = 6/10
Todennäköisyys sille, että pelaaja heittää tässä vaiheessa seiskan, eli kaksi tuplaa, on 6/10. Näin ollen yhden tuplan todennäköisyys on (1/2)*(5/11)*(6/10) = 3/22 = noin 13,6363636 %.
Muuten pelaaja olisi heittänyt kolmannen tuplan. Voimme nyt jättää kolmen erillisen tuplan heittämisen huomiotta merkittävänä tapahtumana. Molempien merkittävien tapahtumien tyyppien todennäköisyydet ovat nyt:
- Mikä tahansa merkittävä tupla = 3/9
- Mikä tahansa seitsemän = 6/9
Todennäköisyys sille, että pelaaja heittää tässä vaiheessa seiskan, eli kaksi tuplaa, on 6/9. Näin ollen yhden tuplan kokonaistodennäköisyys on (1/2)*(5/11)*(4/10)*(6/9) = 2/33 = noin 6,060606 %.
Muuten pelaaja olisi heittänyt neljännen tuplan. Voimme nyt jättää neljän erillisen tuplan heittämisen huomiotta merkittävänä tapahtumana. Molempien merkittävien tapahtumien tyyppien todennäköisyydet ovat nyt:
- Mikä tahansa merkittävä tupla = 2/8
- Mikä tahansa seitsemän = 6/8
Todennäköisyys sille, että pelaaja heittää tässä vaiheessa seiskan, eli kaksi tuplaa, on 6/8. Näin ollen yhden tuplan todennäköisyys on (1/2)*(5/11)*(4/10)*(3/9)*(6/8) = 1/44 = noin 2,272727 %.
Muuten pelaaja olisi heittänyt viidennen tuplan. Voimme nyt jättää viiden erillisen tuplan heittämisen huomiotta merkittävänä tapahtumana. Molempien merkittävien tapahtumien tyyppien todennäköisyydet ovat nyt:
- Mikä tahansa merkittävä tupla = 1/7
- Mikä tahansa seitsemän = 6/7
Todennäköisyys sille, että pelaaja heittää tässä vaiheessa seiskan, eli kaksi tuplaa, on 6/7. Näin ollen yhden tuplan kokonaistodennäköisyys on (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(6/7) = 1/154 = noin 0,649351%.
Muuten pelaaja olisi heittänyt viimeisen jäljellä olevan tuplan. Todennäköisyys tälle on (1/2)*(5/11)*(4/10)*(3/9)*(2/8)*(1/7) = 1/924 = noin 0,108225 %.
Voimme nyt koota kaiken tämän yllä olevaan palautustaulukkoon. Yhdistelmien lukumäärä on enintään 924.
Integraalilaskennan analyysi
Kuvittele, että merkittävien tapahtumien yksi kerrallaan määrittämisen sijaan nopanheitto voi tarkoittaa yksittäisiä hetkiä. Oletetaan, että tapahtumien välinen aika ei säilytä muistia ja että tapahtumien välinen keskimääräinen aika on yksi aikayksikkö. Toisin sanoen tapahtumien välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 1. Tällä ei ole merkitystä vedon ratkaisemisen kannalta, koska tapahtumat tapahtuvat silti yksi kerrallaan.
Tiettyjen tuplasyöksyjen välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on 12. Syy lukuon 12 on se, että jos tapahtuma on merkittävä, on 1/12 todennäköisyys, että kyseessä oli juuri tuo tuplasyöksy. Todennäköisyys sille, että tietty tuplasyöksy ei ole tapahtunut x aikayksikön kuluessa, on exp(-x/12). Todennäköisyys sille, että se on tapahtunut, on siis 1-exp(-x/12).
Olkoon x aikayksiköiden lukumäärä vedonlyönnin aloittamisesta. Todennäköisyys sille, että jokainen tuplaus on tapahtunut ja seiska ei ole tapahtunut, on (1-exp(-x/12)) 6 × exp(-x/2).
Jotta tämä saadaan päätökseen heittämällä 7 hetkellä x, kerro se 1/2:lla, joka on 7:n todennäköisyys, jolloin saat voittotodennäköisyyden täsmälleen hetkellä x ja joka on (1/2) × (1-exp(-x/12)) 6 × exp(-x/2).
Voit löytää voittovedon todennäköisyyden koko ajan integroimalla 1:stä äärettömyyteen:
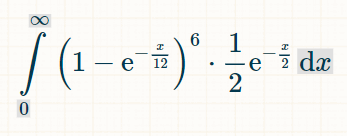
Integrointiin suosittelen tätä integraalilaskuria . Kirjoita integraalikenttään "(1-exp(-x/12))^6*(1/2)*exp(-x/2)." Integroinnin rajojen näet asettamalla asetukset-kohtaan 0 ja ∞. Napsauta sitten "go"."Se antaa sinulle alla olevan integraalin:
(-(1-e^(-x/12))^12+(60*(1-e^(-x/12))^11)/11-12*(1-e^(-x/12))^10+(40 *(1-e^(-x/12))^9)/3-(15*(1-e^(-x/12))^8)/2+(12*(1-e^(-x/12))^7)/7)/2
Meidän ei kuitenkaan tarvitse syöttää siihen nollaa. Laskin antaa vastauksen muodossa 1/924 = noin 0,001082251082251082.
Tässä on viiden eri tuplan integraali. Luku 6 johtuu siitä, että on olemassa kuusi mahdollista tuplaa, joita ei onnistuttu tekemään:
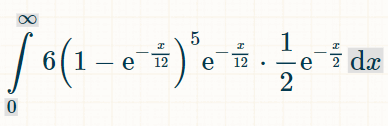
Tässä on todennäköisyys voittaa x aikayksikön sisällä:
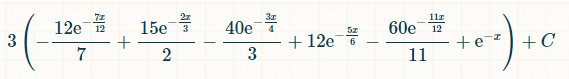
Integroinnin rajalla nollasta äärettömyyteen viiden erillisen tuplaheiton todennäköisyys on 1/154.
Tässä on neljän eri tuplan integraali. Syy lukuun 15 on se, että 6!/(4!*2!) = 15 mahdollista yhdistelmää, joissa on 4/6 tuplaa:
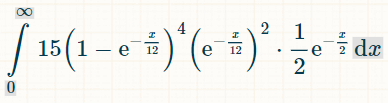
Tässä on todennäköisyys voittaa x aikayksikön sisällä:
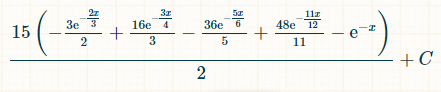
Integroinnin rajat nollasta äärettömyyteen asettavat täsmälleen neljän erillisen tuplaheiton todennäköisyyden 1/44.
Tässä on kolmen erillisen tuplan integraali. Luku 20 johtuu siitä, että kuudesta tuplasta kolmella on 6!/(3!*3!) = 20 mahdollista yhdistelmää:
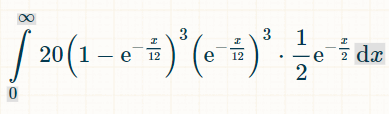
Tässä on todennäköisyys voittaa x aikayksikön sisällä:
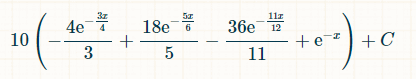
Integroinnin rajat nollasta äärettömyyteen asettavat täsmälleen kolmen erillisen tuplaheiton todennäköisyyden 2/33.



