TV-peliohjelmat - Usein kysytyt kysymykset
Ei se nyt ihan uhkapeliä ole, mutta olen aina miettinyt Price is Right -peliohjelmassa, mikä on paras strategia ison ruletin pyörittämiseen, jos et ole viimeinen pyöräyttäjä. Olettaen, ettet pysty hallitsemaan pyöräytystäsi (täysin satunnainen tulos), 5 sentin askelin 0,05 dollarista 1,00 dollariin, saat yhden pyöräytyksen tai kaksi pyöräytystä yhteensä, etkä voi ylittää 1,00 dollaria. Millä summalla sinun ei pitäisi pyöräyttää toista pyöräytystäsi, jotta sinulla on parhaat mahdollisuudet voittaa jälkeesi pyöräyttävä pelaaja?
Ensimmäisen pelaajan tulee pyöräyttää uudelleen, jos hänen ensimmäinen pyöräytys on 65 senttiä tai vähemmän.
Jos jokin seuraavista ehdoista täyttyy, toisen pelaajan pitäisi pyöräyttää uudelleen.
- Hänen pistemääränsä on pienempi kuin ensimmäisen pelaajan pistemäärä.
- Hänen pisteensä on 50 senttiä tai vähemmän.
- Hänen pistemääränsä on 65 senttiä tai vähemmän ja hän on tasoittanut ensimmäisen pelaajan.
Mikä on optimaalinen strategia Plinko -pelille Price is Right -tilanteessa?
Palkinnot vasemmalta oikealle ovat 100 dollaria, 500 dollaria, 1000 dollaria, 0 dollaria, 10000 dollaria, 0 dollaria, 1000 dollaria, 500 dollaria ja 100 dollaria. Täydellisen analyysin tekemiseksi tarvitsisin tietää tappien tarkan asettelun, mutta pelkästään lautaa silmämääräisesti tarkastelemalla (katso linkki yllä) olen vahvasti sitä mieltä, että pelaajan pitäisi pudottaa kiekko suoraan 10 000 dollarin palkinnon päälle. Vaikka se on reunustettu kahdella nollalla, kaikki muut palkinnot kalpenevat pääpalkinnon rinnalla. Joten pelaajan strategian tulisi olla maksimoida pääpalkinnon todennäköisyys pudottamalla se suoraan sen yläpuolelle. Vahvistaakseni tai kumotakseni hypoteesini tein haun, ja pelin tutkimukseen on omistettu paljon linkkejä. Tämä ( www.amstat.org/publications/jse/v9n3/biesterfeld.html ) on yksi paremmista, mikä on yhdenmukainen johtopäätökseni kanssa. Siinä todetaan muun muassa, että kiekon pudottamisen odotusarvo keskelle on 2557,91 dollaria, keskiosan kummallekin puolelle 2265,92 dollaria ja pienenee siirryttäessä kauemmas keskeltä.
Peliohjelmassa Let's Make a Deal on kolme ovea. Oletetaan esimerkiksi, että kahdesta ovesta paljastuu vuohi ja yhdestä uusi auto. Juontaja Monty Hall valitsee kaksi kilpailijaa valitsemaan oven. Joka kerta, kun Monty avaa ensin oven, jossa on vuohi. Oletetaan, että tällä kertaa se kuului ensimmäiselle kilpailijalle. Vaikka Monty ei koskaan itse asiassa tehnyt tätä, entä jos Monty tarjoaisi toiselle kilpailijalle mahdollisuuden vaihtaa ovea tässä vaiheessa toiseen avaamattomaan oveen. Pitäisikö hänen vaihtaa?
Kyllä! Tämän ongelman ydin on se, että isäntä on ennalta määrätty avaamaan ovi vuohella. Hän tietää, missä ovessa auto on, joten riippumatta siitä, mitkä ovet pelaajat valitsevat, hän voi aina paljastaa ensin vuohen. Kysymys tunnetaan nimellä "Monty Hallin paradoksi". Suuri osa hämmennyksestä johtuu siitä, että usein kysymystä muotoiltaessa ei virheellisesti tehdä selväksi, että isäntä tietää, missä auto on, ja paljastaa aina ensin vuohen. Mielestäni osa syystä on Marilyn Vos Savantin , joka muotoili kysymyksen huonosti kolumnissaan, niskoilla. Oletetaan, että palkinto on oven 1 takana. Seuraavassa on, mitä tapahtuisi, jos pelaajalla (toisella kilpailijalla) olisi strategiana olla vaihtamatta ovea.
- Pelaaja valitsee oven 1 --> pelaaja voittaa
- Pelaaja valitsee oven 2 --> pelaaja häviää
- Pelaaja valitsee oven 3 --> pelaaja häviää
Seuraavassa on, mitä tapahtuisi, jos pelaajalla olisi vaihtostrategia.
- Pelaaja valitsee oven 1 --> Isäntä paljastaa vuohen oven 2 tai 3 takana --> pelaaja vaihtaa toiselle ovelle --> pelaaja häviää
- Pelaaja valitsee oven 2 --> Isäntä paljastaa vuohen oven 3 takana --> pelaaja vaihtaa ovelle 1 --> pelaaja voittaa
- Pelaaja valitsee oven 3 --> Isäntä paljastaa vuohen oven 2 takana --> pelaaja vaihtaa ovelle 1 --> pelaaja voittaa
Joten vaihtamatta jättämisellä pelaajan voittomahdollisuudet ovat 1/3. Vaihtamalla pelaajan voittomahdollisuudet ovat 2/3. Joten pelaajan kannattaa ehdottomasti vaihtaa.
Lisätietoa Monty Hallin paradoksista voi lukea Wikipedian artikkelista.
Kysymykseni koskee ongelmaa, joka tunnetaan nimellä "kahden kirjekuoren paradoksi". Olet peliohjelmassa. Edessäsi on kaksi kirjekuorta, joista kumpikin sisältää tuntemattoman määrän käteistä. Sinulle kerrotaan, että toisessa kirjekuoressa on kaksi kertaa enemmän rahaa kuin toisessa. Sinua pyydetään nyt valitsemaan kirjekuori. Valitset toisen. Se sisältää 50 000 dollaria. Sinulle kerrotaan, että voit pitää valitsemasi kirjekuoren tai vaihtaa sen toiseen. Pitäisikö sinun vaihtaa? Koska tiedät etukäteen, että voit vaihtaa, sillä ei ole väliä, koska valitsisit vain haluamasi kirjekuoren. Mutta koska saat tietää vaihtamisesta vasta kirjekuoren valitsemisen jälkeen, alkuperäinen valinta ja vaihtomahdollisuus ovat kaksi toisistaan riippumatonta tapahtumaa, eikö niin? Kun päätät vaihtaa vai ei, toinen kirjekuori sisältää joko kaksi kertaa enemmän tai puolet nykyisestä summasta. Joten siinä on joko 100 000 dollaria tai 25 000 dollaria. Koska kummankin toteutumisen todennäköisyys on 50 %, toisen kirjekuoren odotusarvo on 62 500 dollaria. Yleisesti ottaen, jos annamme x:n = alun perin valitsemasi määrä, niin toisen kirjekuoren EV on 1,25x. Siksi vaihtaminen on aina oikein. Onko tämä oikein? Kiitos.
Tunnen tämän ongelman hyvin. Käsittelen sitä matemaattisten tehtävien verkkosivustollani, tehtävässä numero 6. Siellä käsittelen yleistä tapausta, mukaan lukien sen, etten katso ensimmäistä kirjekuorta ollenkaan. Vastatakseni kysymykseesi emme kuitenkaan voi jättää huomiotta pelipaikkaa. Sanoit, että se oli "peliohjelma". Useimmissa peliohjelmissa 50 000 dollaria on mukava voitto. Harvat Price is Right -ohjelman kilpailijat pääsevät koskaan niin korkealle. Arvelisin, että alle 50 % Who Wants to be a Millionaire -ohjelman pelaajista pääsee niin korkealle. Samaan aikaan 25 000 dollarin voitot eivät ole epätavallisia peliohjelmissa. Price is Right -ohjelmassa voitetaan rutiininomaisesti autoja, joiden arvo on noin 25 000 dollaria. 32 000 dollarin taso on yleinen voitto Who Wants to be a Millionaire -ohjelmassa. Keskimääräinen voitto Jeopardyssa ohjelmaa kohden on noin 25 000 dollaria. Suuri Ken Jennings ansaitsi keskimäärin vain 34 091 dollaria 74 voitollaan. Eli pointtini on, että 50 000 dollaria on mukava voitto peliohjelmalle, ja 100 000 dollarin voittoja nähdään paljon harvemmin kuin 25 000 dollarin voittoja. Peliohjelma-asiantuntijana olen siis sitä mieltä, että toisessa kirjekuoressa on todennäköisemmin 25 000 dollaria kuin 100 000 dollaria. Joten sanon, että esimerkissäsi on parempi pitää 50 000 dollaria. Se osoittaa myös, ettei voi koskaan olettaa, että todennäköisyys sille, että toisessa kirjekuoressa on puolet tai kaksi kertaa enemmän rahaa, on täsmälleen 50/50. Kun näet summan ja asetat sen pelipaikan kontekstiin, voit tehdä älykkään päätöksen vaihtamisesta, mikä heittää 1,25x-argumentin romukoppaan.
Kysymykseni koskee Australiassa erittäin suosittua Deal or No Deal -nimistä peliohjelmaa, joka on tulossa pian Englantiin. Kilpailijalle näytetään 26 numeroitua salkkua, joista jokaisessa on piilotettu rahasumma, 50 sentistä 200 000 dollariin, kuten alla on esitetty.
- 0,50 dollaria
- 1 dollari
- 2 dollaria
- 5 dollaria
- 10 dollaria
- 25 dollaria
- 50 dollaria
- 75 dollaria
- 100 dollaria
- 150 dollaria
- 250 dollaria
- 500 dollaria
- 750 dollaria
- 1 000 dollaria
- 1 500 dollaria
- 2 000 dollaria
- 3 000 dollaria
- 5 000 dollaria
- 7 500 dollaria
- 10 000 dollaria
- 15 000 dollaria
- 30 000 dollaria
- 50 000 dollaria
- 75 000 dollaria
- 100 000 dollaria
- 200 000 dollaria
Kilpailija valitsee yhden salkuista OMAKSI matkalaukukseensa. Karsintaprosessin kautta hän avaa muut matkalaukut ja yrittää selvittää, kuinka paljon rahaa hänen laukkussaan on vai olisiko viisaampaa ottaa vastaan "pankin tarjous". Pankin tarjoukset perustuvat jäljellä olevien salkkujen aritmeettiseen keskiarvoon, mutta eivät ole samaarvoisia sen kanssa. Joten jos jäljellä on pääasiassa suuria ja arvokkaita salkkuja, on suuri todennäköisyys, että kilpailijan salkku on arvokas, ja siksi pankin tarjous on antelias. Kääntäen, jos pelaaja on ollut vähemmän onnekas ja avannut arvokkaammat salkut, pankin tarjous on alhainen. Mikä olisi paras strategia käyttää, jos olisit kilpailija tässä pelissä? Ei-matemaattinen vaistostrategia olisi jättää pankin tarjoukset huomiotta ja jatkaa laukkujen avaamista, kunnes joko 200 000 dollaria on avattu ja pudonnut tai sekä 100 000 että 75 000 dollaria on avattu ja pudonnut. Mikä on tämän pelin matematiikka, velho?
Deal or No Deal on juuri alkanut täällä Yhdysvalloissa. Säännöt kuulostavat samalta, paitsi että palkintomme nousevat jopa miljoonaan dollariin seuraavasti.
- 0,01
- 1
- 5
- 10
- 25
- 50
- 75
- 100
- 200
- 300
- 400
- 500
- 750
- 1000
- 5000
- 10000
- 25000
- 50000
- 75000
- 100000
- 200 000
- 300000
- 400000
- 500000
- 750000
- 1000000
Tässä on pelin kulku:
- Pelaaja valitsee itselleen yhden tapauksen
- Pelaaja avaa kuusi jäljellä olevista 25 tapauksesta.
- Pankkiiri tekee tarjouksen.
- Jos pelaaja kieltäytyy, hän avaa viisi jäljellä olevista 19 tapauksesta lisää.
- Pankkiiri tekee tarjouksen.
- Jos pelaaja kieltäytyy, hän avaa neljä lisää jäljellä olevista 14 tapauksesta.
- Pankkiiri tekee tarjouksen.
- Jos pelaaja kieltäytyy, hän avaa kolme jäljellä olevasta kymmenestä tapauksesta lisää.
- Pankkiiri tekee tarjouksen.
- Jos pelaaja kieltäytyy, hän avaa kaksi jäljellä olevista seitsemästä tapauksesta lisää.
- Pankkiiri tekee tarjouksen.
- Jos pelaaja kieltäytyy, hän avaa yhden jäljellä olevista koteloista lisää.
- Toista vaiheita 11 ja 12, kunnes pelaaja hyväksyy tarjouksen tai pelaajalla on viimeinen avaamaton laatikko.
Seuraava kaavio esittää pelaajan odotusarvon ja pankkiirin tarjouksen.
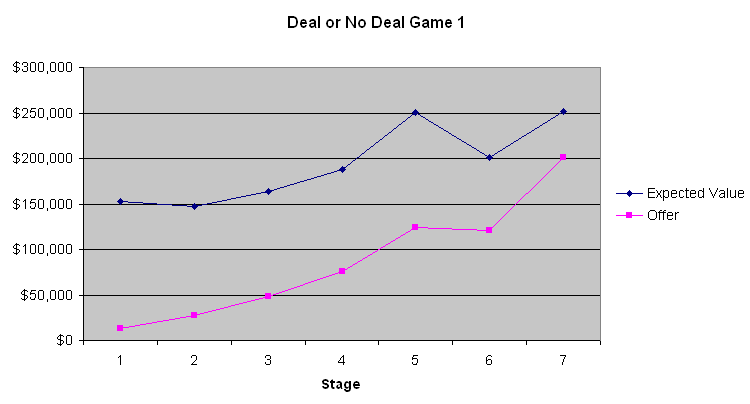
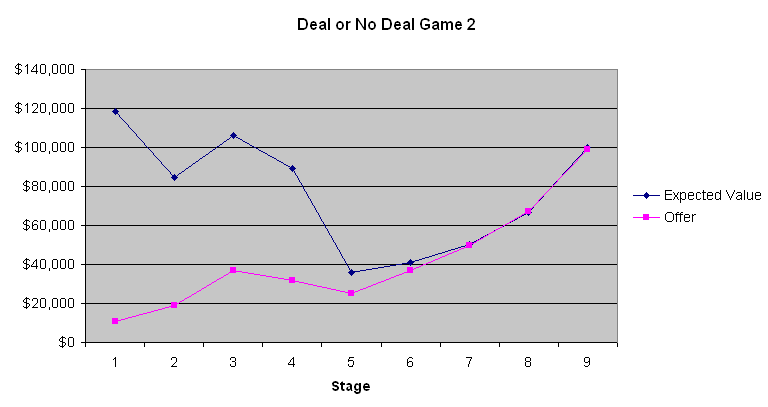
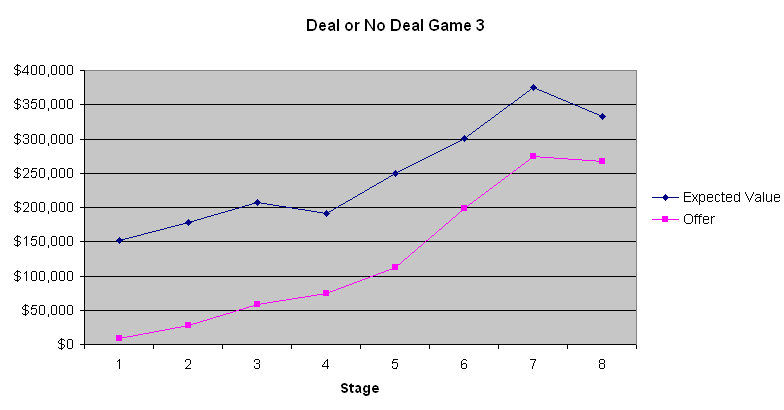
Näistä kolmesta kaaviosta opittavinta on, että ensimmäiset neljästä kuuteen pankkitarjousta ovat kamalia diilejä. Keskimääräisessä matkalaukussa on 131 477,54 dollaria ennen kuin yhtäkään avataan. Ensimmäisessä vaiheessa vain 9 000–13 000 dollarin tarjoaminen on diili, jonka vain hölmö tekisi. Vähitellen tarjoukset kuitenkin paranevat. Peli 2 osoittaa, että odotusarvot olivat lähes samat kuin pankkiirin tarjoamat pelin loppupuolella, kun pelaajan odotusarvo oli melko alhainen. Peleissä 1 ja 3, kun odotusarvot olivat korkeammat, pankkiiri ilmeisesti yritti hyödyntää useimpien ihmisten riskinkarttavaa luonnetta, kun kyseessä ovat suuret summat. En tiedä, oliko sillä merkitystä, mutta pelin 2 kilpailija vaikutti olevan uhkapeluri, joka halusi voittaa isosti. Juontajan kommenttien perusteella, joka kommunikoi pankkiirin kanssa puhelimitse, pankkiiri näyttää ottavan kilpailijoiden sanat ja teot huomioon. Jos olisin pankkiirin asemassa, toimisin suunnilleen samalla tavalla.
Jos pelaaja ei ole riskiä välttelevä eikä riskialtis, ja jättää myös veroseuraamukset huomiotta, pelaajan tulisi kieltäytyä pankkiirin tarjouksista, kunnes yksi ylittää jäljellä olevien matkalaukkujen keskiarvon. Useimmille ihmisille tuloverolain progressiivinen luonne suosii sopimuksen tekemistä. Kuten olen aiemmin sanonut, sanoisin karkeasti sanottavan, että rahan arvo on verrannollinen summan logaritmiin. Joten mitä enemmän varallisuutta sinulla on peliin mennessäsi, sitä taipuvaisempi sinun tulisi olla uhkapelaaja ja kieltäytyä pankkiirin tarjouksista. Kun kyseessä ovat niin suuret summat, mikään strategia ei sovi kaikille. Voin kuitenkin melko varmasti sanoa, että pelaajan tulisi kieltäytyä ensimmäisistä neljästä kuuteen tarjousta ja sitten hyväksyä tarjoukset tapauskohtaisesti (sanaleikki tarkoituksella).
Linkit:
Voit katsoa Deal or No Dealin NBC.comissa.
Aikaisempien esitysten arkisto .
Katson peliä "Deal or no Deal". Ymmärrän, että pankkiirin "tarjous" on vain tapausten jäljellä olevien arvojen jakaminen tapausten lukumäärällä [pyöristys plus-miinus]. Onko tässä pelissä MITÄÄN strategiaa, vai onko "sopimus" aina vain hyväksyttävä asia? Riippuuko se siitä, kuinka monta tapausta sinulla on avattavana tai jotain?
Kuten 26. joulukuuta 2005 julkaistussa kolumnissani osoitan, pankkiirin tarjous on yleensä paljon pienempi kuin jäljellä olevien tapausten keskiarvo. Jos se kuitenkin aina olisi niin, jokaisella strategialla olisi sama odotusarvo. Pelaaja olisi välinpitämätön jokaisen tarjouksen suhteen.
"Sopii tai ei sovi" -tilanteen alussa todennäköisyys valita miljoonan dollarin tapaus on 1/26. Kun kaikki muut paitsi yksi tapaus on poistettu, mikä on todennäköisyys sille, että tapaukseni sisältää miljoona dollaria? Onko se 50/50 vai edelleen 1/26?
50-50
Ei. Monet ihmiset väittelevät kanssani tästä. Monet kirjoittajat väittävät, että todennäköisyydet eivät voi muuttua, jos lisätään tietoa. Joten jos todennäköisyys alkaa arvosta 1:26, sen täytyy pysyä siinä. Toisin kuin vedonlyöntijärjestelmien myyjät sanovat, todennäköisyydet voivat todellakin muuttua, kun lisätään tietoa. En halua yrittää opettaa tässä perusasioita todennäköisyydestä, mutta mikä tahansa korkeakoulutason matematiikan kirja ehdollisesta todennäköisyydestä tai Bayesin lauseesta kattaa tämän aiheen hyvin.
Selitänpä, mitä tapahtui Let's Make a Deal -ohjelmassa. Kilpailija valitsisi yhden kolmesta esiripusta. Yhdessä olisi erittäin arvokas palkinto ja kahdessa muussa pienempää palkintoa. Väittelyn vuoksi oletetaan, että toisen esiripun takana olisi auto ja kahden muun takana vuohi. Sitten Monty avaisi aina, toistan AINA, toisen kahdesta valitsemattomasta esiripusta paljastaakseen vuohen. Satojen esitysten jälkeen tämä viittaisi siihen, että Monty Hall (juontaja) tiesi missä auto oli ja avasi tarkoituksella esiripun, joka paljasti vuohen. Ilmeisesti, kun pelaaja valitsi esiripun, todennäköisyys sille, että se piti autoa sisällään, oli 1/3 ja todennäköisyys sille, että toinen kahdesta valitsemattomasta esiripusta piti autoa sisällään, oli 2/3. Monty on sitten ennalta määrätty avaamaan valitsemattoman esiripun, joka sisältää maalin. Ennalta määrätty on tässä avainsana. Koska Monty ei voi avata pelaajan esiripua tässä vaiheessa, pelaajan esiripun todennäköisyys paljastaa auton pysyy 1/3:ssa. Todennäköisyys sille, että valitsematon esiripun paljastaa auton, pysyy 2/3:ssa, mutta nyt kaikki on yhden esiripun päällä. Joten vuohen paljastumisen jälkeen todennäköisyys, että pelaajan verholla on auto, on 1/3 ja todennäköisyys, että toisella avaamattomalla verholla on auto, on 2/3, joten vaihtaminen on viisas valinta.
Seuraava taulukko näyttää kaikki mahdolliset lopputulokset. Tapauksessa, jossa pelaaja valitsi verhon, jossa on auto, pyysin Montya avaamaan verhon mielivaltaisesti. Kuten näet, vaihtamatta jättäminen johtaa 1/3 voittotodennäköisyyteen ja vaihtaminen 2/3 voittotodennäköisyyteen.
Tehdään sopimus
| Pelaaja Valitsee | Auto | Verho Avattu | Todennäköisyys | Voita Vaihtaminen |
| 1 | 1 | 1 | 0 % | ei saatavilla |
| 1 | 1 | 2 | 5,56 % | N |
| 1 | 1 | 3 | 5,56 % | N |
| 1 | 2 | 1 | 0 % | ei saatavilla |
| 1 | 2 | 2 | 0 % | ei saatavilla |
| 1 | 2 | 3 | 11,11 % | Y |
| 1 | 3 | 1 | 0 % | ei saatavilla |
| 1 | 3 | 2 | 11,11 % | Y |
| 1 | 3 | 3 | 0 % | ei saatavilla |
| 2 | 1 | 1 | 0 % | ei saatavilla |
| 2 | 1 | 2 | 0 % | ei saatavilla |
| 2 | 1 | 3 | 11,11 % | Y |
| 2 | 2 | 1 | 5,56 % | N |
| 2 | 2 | 2 | 0 % | ei saatavilla |
| 2 | 2 | 3 | 5,56 % | N |
| 2 | 3 | 1 | 11,11 % | Y |
| 2 | 3 | 2 | 0 % | ei saatavilla |
| 2 | 3 | 3 | 0 % | ei saatavilla |
| 3 | 1 | 1 | 0 % | ei saatavilla |
| 3 | 1 | 2 | 11,11 % | Y |
| 3 | 1 | 3 | 0 % | ei saatavilla |
| 3 | 2 | 1 | 11,11 % | Y |
| 3 | 2 | 2 | 0 % | ei saatavilla |
| 3 | 2 | 3 | 0 % | ei saatavilla |
| 3 | 3 | 1 | 5,56 % | N |
| 3 | 3 | 2 | 5,56 % | N |
| 3 | 3 | 3 | 0 % | ei saatavilla |
Deal or No Dealissa mikään ei ole ennalta määrättyä. Oletetaan, että Deal or No Dealissa jäljellä olevat summat olivat 0,01 dollaria, 1 dollari ja 1 000 000 dollaria. Kolmen jäljellä olevan tapauksen jälkeen ON mahdollista, että avattu tapaus sisältää miljoona dollaria. Seuraava taulukko näyttää mahdolliset lopputulokset, kun jäljellä on kolme tapausta. Muista, että pelaaja ei voi avata omaa tapaustaan.
Sopimus tai ei sopimusta
| Pelaaja Valitsee | Miljoona dollaria | Tapaus Avattu | Todennäköisyys | Voita Vaihtaminen |
| 1 | 1 | 1 | 0 % | ei saatavilla |
| 1 | 1 | 2 | 5,56 % | N |
| 1 | 1 | 3 | 5,56 % | N |
| 1 | 2 | 1 | 0 % | ei saatavilla |
| 1 | 2 | 2 | 5,56 % | Toivoton |
| 1 | 2 | 3 | 5,56 % | Y |
| 1 | 3 | 1 | 0 % | ei saatavilla |
| 1 | 3 | 2 | 5,56 % | Y |
| 1 | 3 | 3 | 5,56 % | Toivoton |
| 2 | 1 | 1 | 5,56 % | Toivoton |
| 2 | 1 | 2 | 0 % | ei saatavilla |
| 2 | 1 | 3 | 5,56 % | Y |
| 2 | 2 | 1 | 5,56 % | N |
| 2 | 2 | 2 | 0 % | ei saatavilla |
| 2 | 2 | 3 | 5,56 % | N |
| 2 | 3 | 1 | 5,56 % | Y |
| 2 | 3 | 2 | 0 % | ei saatavilla |
| 2 | 3 | 3 | 5,56 % | Toivoton |
| 3 | 1 | 1 | 5,56 % | Toivoton |
| 3 | 1 | 2 | 5,56 % | Y |
| 3 | 1 | 3 | 0 % | ei saatavilla |
| 3 | 2 | 1 | 5,56 % | Y |
| 3 | 2 | 2 | 5,56 % | Toivoton |
| 3 | 2 | 3 | 0 % | ei saatavilla |
| 3 | 3 | 1 | 5,56 % | N |
| 3 | 3 | 2 | 5,56 % | N |
| 3 | 3 | 3 | 0 % | ei saatavilla |
Deal or No Deal -taulukko osoittaa, että kun jäljellä on kolme tapausta, todennäköisyys sille, että pelaaja avaa miljoonan dollarin tapauksen, on 1/3 (toivoton voitto), pelaajaa vaihtavan pelaajan voiton todennäköisyys on 1/3 ja pelaajaa vaihtavan pelaajan häviön todennäköisyys on 1/3. Näin ollen todennäköisyys tapausten vaihtamiselle on sama. Kun tapauksia on jäljellä enää kaksi, todennäköisyys sille, että kumpikin tapaus sisältää suuremman palkinnon, on 50/50.
Aika uudelle "sopitaan vai ei" -kysymykselle. Oletetaan, että kaikkien pankkiirin ja Celine Dionin sopimuksien jälkeen sinulle jää kaksi matkalaukkua, 500 000 dollarin ja 1 000 000 dollarin. Pankkiirin tarjous on luultavasti hieman alle 750 000 dollaria. Kumman valitsisit? Entä jos kaksi jäljellä olevaa salkkua olisivat 0,01 dollarin ja 1 000 000 dollarin salkku? Luulen, että kyse on kokonaan uhkapelurista vai et, eikä sillä oikeastaan ole mitään tekemistä kertoimien kanssa. Kysyn tätä siksi, että mietin, voittaako KUKAAN koskaan 1 000 000 dollaria (vaikka he olisivatkin valinneet taikasalkun).
Kun palkinnoista tulee elämää mullistavia summia, viisaan pelaajan tulisi pelata varovaisesti odotusarvon maksimoimisen kustannuksella. Hyvän strategian tulisi olla odotetun onnellisuuden maksimointi. Hyvä funktio onnellisuuden mittaamiseen on mielestäni kokonaisvarallisuuden logaritmi. Otetaan henkilö, jonka nykyinen varallisuus on 100 000 dollaria, ja hänelle esitetään kaksi tapausta: 0,01 dollaria ja 1 000 000 dollaria. Jos sopimusta ei hyväksytä, odotettu onnellisuus on 0,5 * log (100 000,01 dollaria) + 0,5 * log (1 100 000 dollaria) = 5,520696. Olkoon b pankin tarjous, jonka vastaanottamisesta pelaaja on välinpitämätön.
log(b) = 5,520696
b = 10 5,520696
b = 331 662,50 dollaria.
Joten tämän hypoteettisen pelaajan pitäisi suhtautua välinpitämättömästi pankin 331 662,50 dollarin tarjoukseen. Mitä pienempi varallisuutesi on pelin alkaessa, sitä varovaisemmin sinun tulisi pelata. Yleensä pelin loppuvaiheessa pankin tarjoukset ovat lähellä odotusarvoa, joskus hieman enemmän, vähän enemmän. Ainoa rationaalinen tapaus, jossa pelaaja voisi voittaa miljoonan, on, jos hänellä oli paljon varallisuutta pelin alkaessa ja/tai pankin tarjoukset olivat epätavallisen kitsaita. Tuottajat tuntuvat pitävän ahkerista keskiluokan ihmisistä, joten tuskin näemme ketään, jolla on varaa olla huoleton, kun kyseessä ovat suuret summat. En ole myöskään koskaan nähnyt pankin tekevän tarjouksia, jotka ovat alle 90 % odotusarvosta pelin loppuvaiheessa. Se hetki, kun näemme jonkun voittavan miljoonan, on silloin, kun peliin astuu rappeutunut uhkapeluri, joka ei pysty lopettamaan. Kun niin tapahtuu, kannustan pankkiiria.
Tämä on jatkoa Deal or No Deal -ohjelmalle, jota katsoin ensimmäistä kertaa äskettäin. Analyysisi olettaa, että talo ei tiedä matkalaukun rahan arvoa. Katsomassani ohjelmassa loppupelissä molemmat kilpailijat olivat kuitenkin valinneet arvokkaan tapauksen, ja molemmille tarjottiin (tai olisi tarjottu, koska toinen oli jo lopettanut) odotettua arvoa (EV) suurempia diilejä. Äärimmäisessä tapauksessa pelaajalle "olisi tarjottu" 687 000 dollaria, kun jäljellä olevat kaksi dollarimäärää olivat 500 000 ja 750 000 dollaria. Ainoa rationaalinen selitys tälle on, että pankkiiri tietää pelaajan matkalaukun arvon ja tarjotut diilit perustuvat siihen.
Vain minun kaksi senttiäni, eikä vastausta tarvita.
Kiitos, ettet odottanut vastausta, mutta yleensä vastaan kyllä peliohjelmien kysymyksiin. Joka jaksossa väitetään, että laatikoiden summat on sijoitettu satunnaisesti, eikä Howie eikä pankkiiri tiedä tuloksia. Tätä ei koskaan väitetty Let's Make a Deal -ohjelmassa, jossa Monty Hall selvästi tiesi. Minäkin olen nähnyt pankkiirin tarjoavan odotettua enemmän arvoa viimeisenä tarjouksena, varsinkin kun kyseessä ovat suuret summat. Olen vahvasti sitä mieltä, ettei tämä johdu siitä, että pankkiiri tietäisi, mitä pelaajan laatikossa on. 1950-luvulla oli valtava skandaali, kun tuli ilmi, että ohjelma 21 , kuten muutkin, oli fixoitu. Ei ole mitään pakottavaa syytä pilata onnistunutta ohjelmaa ja kaikkien peliohjelmien rehellisyyttä kahlata palkintorahoja pankkien tarjousten kautta.
Voin esittää kolme teoriaa siitä, miksi pankkiiri tarjoaa joskus enemmän kuin jäljellä olevien tapausten keskiarvo.
- Sarjassa yritetään kuvata pankkiiria toimistossaan hikoilemassa. Howie Mandel kommentoi usein pankkiirin mielialaa ja äänensävyä. Ehkä sarjasta tekee dramaattisemman ajatella pankkiiria riskiä karttavana rahojen laskijana, joka mieluummin minimoi tappionsa kuin ottaa riskin jakamalla suuren palkinnon.
- Oikea pankkiiri todellakin välttelee riskejä. Tämä menee asiantuntemukseni ulkopuolelle, mutta käsitykseni mukaan peli- ja tosi-tv-ohjelmat tuottaa yleensä televisioverkosta riippumaton yritys. Nämä pienemmät yritykset etsivät vakuutusyhtiön pienentääkseen kilpailijoiden riskiä voittaa suurempia palkintoja. Tällaisessa tapauksessa vakuutusyhtiö olisi oikea pankkiiri ja saattaisi vaikuttaa pankkiirin käyttäytymiseen ohjelmassa. Vakuutusyhtiöt, jotka vakuuttavat tällaisia epätavallisia asioita, eivät ole jättimäisiä ja saattavat mieluummin pelata varman päälle, kun kyseessä ovat suuret summat.
Esimerkissäsi pankkiirin tarjous oli 9,92 % odotusarvoa suurempi. Jos pankkiiri olisi noudattanut Kellyn kaavaa , tällainen tarjous olisi tehty vain 782 008 dollarin kokonaispelikassalla, joka on vähemmän kuin enimmäispalkinto. Yksikään itseään kunnioittava vakuutusyhtiö ei olisi niin varovainen. Pelkkä tämä syy ei selvästikään voi oikeuttaa esimerkissäsi esitettyä tarjousta.
- Ohjelma yrittää saada kilpailijat näyttämään tyhmiltä ja ahneilta. Ohjelmat kuten Are You Smarter than a Fifth Grader ja Tonight Show'n "Jaywalking" eivät olisi menestyneitä, jos emme löytäisi tyydytystä nauramalla tietokilpailussa kyseenalaistetuille. Ohjelmat Friend or Foe ja The Weakest Lenk olivat erinomaisia ihmisluonnon ahneuden paljastamisessa. Minun on tunnustettava tuntevani vahingoniloa , kun kilpailija kieltäytyy odotettua suuremmasta tarjouksesta ja hyväksyy pienemmän summan.
Mielestäni syynä on näiden kolmen yhdistelmä, mutta pääasiassa kolmas.
Jos lopettaisin tämän vastauksen tähän, olen varma, että saisin kommentteja, joissa kyseenalaistettaisiin, olisiko hypoteettisia pankkiirien tarjouksia todella tehty. Tämä viittaa siihen, että ne ovat paisuteltuja dramaattisen vaikutelman saavuttamiseksi. Olen tallentanut 13 pelin yksityiskohdat. Yhdessä niistä, jossa oli jäljellä kolme tapausta (1 000 dollaria, 5 000 dollaria ja 50 000 dollaria), keskiarvo oli 18 667 dollaria ja tarjous oli 21 000 dollaria. Tämä on 12,5 % yli odotusarvon. Toisessa esityksessä, jossa oli jäljellä kaksi tapausta (400 dollaria ja 750 000 dollaria), keskiarvo oli 375 200 dollaria ja tarjous oli 400 000 dollaria. Tämä on 6,6 % yli odotusarvon. Joten en näe mitään syytä kyseenalaistaa hypoteettisten tarjousten rehellisyyttä.
Linkit:
Deal or No Deal -kaava : Tämä sivu näyttää vanhoja ja uusia kaavoja pankkiirin tarjouksen laskemiseksi Deal or No Deal -verkkosivuston ilmaisen pelin perusteella.
Kuinka paljon lyöisit vetoa kunkin henkilön asemassa Final Jeopardyssa näillä tuloksilla:
Pelaaja A: 10 000 dollaria
Pelaaja B: 8 000 dollaria
Pelaaja C: 3 500 dollaria
Aloitan tekemällä muutamia oletuksia. Ensinnäkin oletan, että kolmella pelaajalla ei ole aiempaa tietoa vedonlyöntikäyttäytymisestä Final Jeopardyssa, lukuun ottamatta esitettyyn taulukkoon perustuvia todennäköisyyksiä. Toiseksi oletan, että kategorian tuntemisesta ei ole apua. Kolmanneksi oletan myös, että kaikki kolme kilpailijaa haluavat tavoitella voittoa eivätkä halua ottaa toista pelaajaa mukaan tasatilanteessa.
Aloitetaan pelaajasta C. Hänen pitäisi odottaa, että A saattaa panostaa 6001 dollaria pysyäkseen B:n yläpuolella, jos B on oikeassa. Jos A on kuitenkin väärässä, se laskisi hänen panoksensa 3999 dollariin. Tällaisessa tilanteessa C:n pitäisi panostaa vähintään 500 dollaria ja olla oikeassa voittaakseen A:n. Mielestäni kuitenkin, jos sinun on oltava oikeassa voittaaksesi, voit yhtä hyvin panostaa ison panoksen. Joten jos olisin CI, panostaisin kaiken.
B on ristiriidassa ison ja pienen panoksen välillä. Pienen panoksen tulisi olla 999 dollaria tai vähemmän, jotta se pysyisi C:n yläpuolella, jos C on oikeassa. Pienen panoksen etuna on pysyä C:n yläpuolella joka tapauksessa ja toivoa, että A:n panos on iso ja väärä. Suuren panoksen ei välttämättä tarvitse olla koko matka, mutta se voi yhtä hyvin olla. Suuren panoksen etuna on toivoa, että joko A:n panos on pieni tai iso ja väärä, mutta molemmat edellyttävät, että B on oikeassa.
A haluaa pohjimmiltaan mennä samaan suuntaan kuin B. A:n pieni panos voi olla mitä tahansa 0 dollarista 1000 dollariin, ja se pysyy B:n yläpuolella, jos B panostaa 999 dollaria. Ison panoksen tulisi olla 6001 dollaria, jotta voitto taataan A:n ollessa oikeassa, ja toivo säilyy, jos B panostaa ison summan ja kaikki kolme pelaajaa ovat väärässä.
Jotta voisin arvioida oikeiden ja väärien vastausten kahdeksan mahdollisen lopputuloksen todennäköisyyksiä, tarkastelin j-archive.com-sivustolta (ei enää saatavilla) löytyviä Jeopardy-pelin lopputuloksia kausilta 20–24. Näin tulokset näyttävät: pelaaja A on johdossa, jota seuraa pelaaja B ja C viimeisenä.
Mahdollisia lopputuloksia lopullisessa vaarassa
| Pelaaja A | Pelaaja B | Pelaaja C | Todennäköisyys |
| Oikea | Oikea | Oikea | 21,09 % |
| Oikea | Oikea | Väärin | 9,73 % |
| Oikea | Väärin | Oikea | 10,27 % |
| Väärin | Oikea | Oikea | 8,74 % |
| Oikea | Väärin | Väärin | 13,33 % |
| Väärin | Oikea | Väärin | 10,27 % |
| Väärin | Väärin | Oikea | 8,63 % |
| Väärin | Väärin | Väärin | 17,92 % |
Käyttämällä sivustollani mathproblems.info tehtävässä 192 selittämääni peliteorian logiikkaa huomaan, että A:n ja B:n tulisi satunnaistaa strategiansa seuraavasti.
Pelaajan A tulisi panostaa ison panoksen todennäköisyydellä 73,6 % ja pienen 26,4 %.
Pelaajan B tulisi panostaa ison panoksen todennäköisyydellä 67,3 % ja pienen panoksen todennäköisyydellä 32,7 %.
Pelaajan C tulisi panostaa isosti todennäköisyydellä 100,0 %.
Jos tätä strategiaa noudatetaan, kunkin pelaajan voittotodennäköisyys on seuraava:
Pelaaja A: 66,48 %
Pelaaja B: 27,27 %
Pelaaja C: 6,25 %
Sivuhuomautuksena, yllä olevan taulukon perusteella todennäköisyys sille, että johtaja arvaa Final Jeopardy -tehtävän oikein, on 54,4 %, toiseksi sijoittuneella pelaajalla 49,8 % ja kolmanneksi sijoittuneella 48,7 %. Kokonaistodennäköisyys on 51,0 %.
Käytännön vinkkinä, pelaajilla on tietoa vedonlyöntikäyttäytymisestä. Mielestäni pelaajat panostavat usein isoja summia useammin kuin se olisi matemaattisesti perusteltua. Mielenkiintoista kyllä, pidän panostamista Daily Doublessa liian varovaisena kuin matemaattisesti perusteltuna. Yksi syy siihen, miksi uskon Ken Jenningsin menestyneen niin hyvin, oli aggressiivinen panostaminen Double Doublesissa. Joka tapauksessa, jos olisin ohjelmassa mukana, olettaisin, että kaksi muuta pelaajaa panostaisivat aggressiivisesti. Joten todelliset panokseni olisivat 6000 dollaria A:lle (olen kiltti B:lle), 0 dollaria B:lle ja 3495 dollaria C:lle (jättäen hieman panostamatta siltä varalta, että A tyhmästi panostaa kaiken tai kaikki paitsi 1 dollarin ja on väärässä).
Ennen kuin joku kyseenalaistaa minut siinä, miten satunnaisluku voidaan arpoa oikeassa paikassa, ehdotan Stanford Wongin strategiaa, jossa kellon sekuntiviisaria käytetään satunnaisluvun arpomiseen väliltä 1–60.
Uusi peliohjelma nimeltä " Colour of Money " on saanut ensi-iltansa Isossa-Britanniassa. Yksinäiselle kilpailijalle annetaan satunnaisesti tavoitesumma, jonka tiedetään vaihtelevan 55 000 punnan ja 79 000 punnan välillä. Rahan ansaitsemiseksi hän valitsee 10 pankkiautomaattia 20:stä, joista jokaisessa on 1 000–20 000 puntaa, parillisin 1 000 punnan välein. Kun hän valitsee laitteen, se alkaa laskea ylöspäin 1 000 punnasta 1 000 punnan välein.
Pelaaja voi huutaa "Stop!" milloin tahansa, ja hän laittaa pankkiinsa näytöllä näkyvän summan. Jos pelaaja ei pysähdy ajoissa ja koneesta loppuvat rahat, hän ei laita pankkiinsa mitään. Emäntä tarjoaa tilastoja, kuten jäljellä olevien valittavien koneiden lukumäärän, jäljellä olevan ansaittavan summan, keskimäärin tarvittavan summan konetta kohden voittaakseen ja kuinka paljon summia koneissa on jäljellä.
Pelaaja voi "pelata aukkoja" siinä mielessä, että jos on valittu useita koneita, esimerkiksi 4 000 puntaa, 5 000 puntaa ja 6 000 puntaa, koneen panos nousee taatusti 7 000 puntaan, kun se ylittää 3 000 punnan rajan. Kysymykseni kuuluu, millaista strategiaa pelaajan tulisi käyttää?
Tällaisten asioiden analysointiin voisin käyttää viikkoja. Valitettavasti luin viestisi lähes kolme kuukautta kirjoituksesi jälkeen, koska "kysy velholta" -kysymyksiä oli niin paljon jäljellä. Wikipedian sivun perusteella näyttää siltä, että kyseinen ohjelma oli floppi ja se peruttiin. Se on kuitenkin edelleen mielenkiintoinen ongelma.
Tarjoilija kertoo kätevästi, kuinka paljon jäljellä olevaa peliä keskimäärin tarvitset peliautomaattia kohden, jotta pääset peliisi. Tuntien raapustuksen jälkeen en keksi parempaa vaihtoehtoa kuin asettaa pysähdysten tavoitteeksi noin 25 % korkeamman määrän kuin vaadittu keskiarvo. Se on vain perusteltu arvaus, joten älä pyydä minua todistamaan, että se on optimaalinen. Kuten totesit, aja myös taukojen yli äläkä koskaan pysähdy juuri ennen jo poimittua määrää.
Kun jäljellä on vain kaksi automaattia ja tarvittava summa on 13 000 puntaa tai vähemmän, yrittäisin saada sen kokonaan toiseksi viimeisellä automaatilla. Jos summa on 14 000 puntaa tai enemmän, yrittäisin saada puolet siitä seuraavalla automaatilla.
Jos he tuovat tämän sarjan takaisin, toivon, että brittiläiset lukijani ilmoittavat minulle siitä. Tämänkaltaiseen pulmaan voisin jäädä pakkomielteeksi, kuten Eternity-pulmaan , joka sattumalta (tai sitten ei) oli myös muualla kuin Isossa-Britanniassa.
PS Miksi sana "colour" kirjoitetaan Isossa-Britanniassa au-kirjaimella? Se ei ole minusta järkevää.
Mikä on keskimääräinen palkinto lyöntiä kohden ja optimaalinen strategia Punch a Bunch -pelissä The Price is Right -sivustolla?
Niille, jotka eivät tunne sääntöjä, ne selitetään Price Is Right -verkkosivustolla . Jos et ole perehtynyt peliin, käytä hetki aikaa käydäksesi siellä, koska oletan sinun tuntevan säännöt. Pelistä on myös useita YouTube-videoita. Tässä on vanha video , jossa näytetään toinen mahdollisuus, mutta tuolloin maksimipalkinto oli vain 10 000 dollaria. Nyt se on 25 000 dollaria.
Lasketaan ensin sellaisen voiton odotusarvo, johon ei liity toista mahdollisuutta. Seuraava taulukko osoittaa, että keskiarvo on 1371,74 dollaria.
Punch a Bunch -palkintojenjako ilman toista mahdollisuutta
| Palkinto | Määrä | Todennäköisyys | Odotettu voitto |
| 25000 | 1 | 0,021739 | 543.478261 |
| 10000 | 1 | 0,021739 | 217.391304 |
| 5000 | 3 | 0,065217 | 326.086957 |
| 1000 | 5 | 0.108696 | 108.695652 |
| 500 | 9 | 0,195652 | 97.826087 |
| 250 | 9 | 0,195652 | 48.913043 |
| 100 | 9 | 0,195652 | 19.565217 |
| 50 | 9 | 0,195652 | 9.782609 |
| Kokonais | 46 | 1.000000 | 1371.739130 |
Toiseksi, laske keskimääräinen palkinto, jolla on toinen mahdollisuus. Seuraava taulukko osoittaa, että keskimääräinen palkinto on 225 dollaria.
Punch a Bunch -palkintojenjako Second Chancen avulla
| Palkinto | Määrä | Todennäköisyys | Odotettu voitto |
| 500 | 1 | 0,250000 | 125.000000 |
| 250 | 1 | 0,250000 | 62,500000 |
| 100 | 1 | 0,250000 | 25.000000 |
| 50 | 1 | 0,250000 | 12,500000 |
| Kokonais | 4 | 1.000000 | 225.000000 |
Kolmanneksi, luo odotusarvotaulukko pelaajan löytämien toisten mahdollisuuksien lukumäärän perusteella. Tämä voidaan löytää yksinkertaisella matematiikalla. Esimerkiksi kahden toisen mahdollisuuden todennäköisyys on (4/50) × (3/49) × (46/48). Odotusarvo s toisella mahdollisuudella on 1371,74 dollaria + s × 225 dollaria. Seuraava taulukko näyttää todennäköisyyden ja keskimääräisen voiton 0–4 toiselle mahdollisuudelle.
Punch a Bunch -palkintojen palautustaulukko
| Toiset mahdollisuudet | Todennäköisyys | Keskimääräinen voitto | Odotettu voitto |
| 4 | 0.000004 | 2271.739130 | 0,009864 |
| 3 | 0.000200 | 2046.739130 | 0.408815 |
| 2 | 0,004694 | 1821.739130 | 8.551020 |
| 1 | 0,075102 | 1596.739130 | 119.918367 |
| 0 | 0,920000 | 1371.739130 | 1262.000000 |
| Kokonais | 1.000000 | 1390.888067 |
Keskimääräinen voitto lyöntiä kohden (mukaan lukien toisista mahdollisuuksista saadut lisärahat) on siis 1390,89 dollaria.
Seuraava taulukko näyttää strategiani hyväksyttävän vähimmäisvoiton suhteen jäljellä olevien lyöntien määrän mukaan. Huomaa, että pelaaja voi päästä 1 400 dollariin palkinnoilla 1 000 dollaria + 250 dollaria + 100 dollaria + 50 dollaria kolmen toisen mahdollisuuden kautta.
Punch a Bounce -strategia
| Jäljellä olevat lyönnit | Minimi seisomaan |
| 3 | 5 000 dollaria |
| 2 | 5 000 dollaria |
| 1 | 1 400 dollaria |
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mikä olisi optimaalinen strategia rahojesi jakamiseen Million Dollar Money Drop -peliohjelmassa, jos et ole varma vastauksesta?
Muiden lukijoiden hyödyksi, haluan ensin tarkistaa säännöt.
- Pelaajajoukkue aloittaa 1 000 000 dollarilla.
- Joukkueelle annetaan monivalintakysymys.
- Joukkueen on jaettava rahansa mahdollisten vastausten kesken. Oikeaan vastaukseen panostettu raha siirtyy seuraavaan kysymykseen.
- Joukkueen on suljettava kokonaan pois ainakin yksi mahdollinen vastaus olemalla panostamatta siihen rahaa.
- Tämä prosessi toistuu useiden kierrosten ajan. Pelaajalle annetaan myös yksi mahdollisuus muuttaa mieltään.
Jos joukkue on varma vastauksesta, hänen tulisi tietenkin panostaa kaikki rahansa oikeaan vastaukseen. Jos joukkue pystyy rajaamaan vastauksen kahteen, mutta antaa kummallekin 50 %:n todennäköisyyden olla oikea, heidän tulisi jakaa rahansa tasan kahden vaihtoehdon kesken.
Vaikeammaksi tilanne muuttuu, jos joukkue kallistuu yhden vastauksen puoleen, mutta ei sulje täysin pois yhtä tai useampaa muuta. Katsotaanpa esimerkkiä. Oletetaan, että joukkue määrittää kunkin oikean vastauksen todennäköisyyden seuraavasti: A 10 %, B 20 %, C 30 %, D 40 %. Miten heidän tulisi jakaa hänen rahansa?
Väitän, että vastaus on noudattaa Kellyn kaavaa . Lyhyesti sanottuna joukkueen tulisi maksimoida hänen varallisuutensa logaritmi jokaisella kysymyksellä. Tätä varten sinun on otettava huomioon, kuinka paljon varallisuutta sinulla jo on.
Oletetaan, että nykyinen varallisuutesi, jonka olet kerännyt ohjelmasta riippumatta, on 100 000 dollaria. Tämä on ensimmäinen kysymyksesi, joten sinulla on 1 000 000 dollaria ohjelmarahaa jaettavana. Ensin poista vaihtoehto, jolla on pienin todennäköisyys, ohjelman sääntöjen mukaisesti. Sitten haluat maksimoida 0,2 × log(100 000 + b * 1 000 000) + 0,3 × log(100 000 + c * 1 000 000) + 0,4 × log(100 000 + d * 1 000 000), jossa pienet a, b ja c viittaavat kunkin vastauksen osuuteen.
Tämä voitaisiin ratkaista differentiaali- ja integraalilaskennalla ja ratkaisemalla trinomiyhtälö, kokeilemalla ja erehtymällä tai mieluummin Excelin "tavoitteen etsintä" -toiminnolla. Käytitpä mitä tahansa menetelmää, oikea vastaus on laittaa 18,9 % B:hen, 33,3 % C:hen ja 47,8 % D:hen.
Tietenkään kukaan ohjelmassa ei pysty tekemään kaikkea tätä matematiikkaa annetussa ajassa, puhumattakaan siitä, että sinun on myös siirrettävä paljon käteistä tuona aikana. Käytännöllisempi neuvoni on jakaa rahat suhteessa vastauksen todennäköisyyden arvioosi olettaen, että epätodennäköisin vaihtoehto ei ole mahdollinen. Esimerkissä tämä johtaisi 22,2 %:n jakautumiseen B:lle, 33,3 %:n jakautumiseen C:lle ja 44,4 %:n jakautumiseen D:lle.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Michiganin arpajaisissa on kolmen pelaajan peli, jossa on seuraavat säännöt: Onko tässä pelissä viimeisenä pelaamisesta mitään pelipaikkaetua? Mikä on optimaalinen strategia kullekin pelaajalle? Tässä onYouTube- video, joka näyttää pelin.
Ensinnäkin viimeisenä toimimisesta ei ole asemaetua. Koska pelaajat pidetään äänieristetyssä kopissa aiempien pelaajien pelatessa, järjestyksellä ei ole väliä.
Toiseksi pelissä on oltava Nash-tasapainotila, jossa strategia, jossa pysytään vähintään x pisteen pistemäärällä, on parempi kuin mikään muu strategia. Kysymys on x:n löytämisestä.
Kysyin itseltäni, mikä olisi strategia, jos jokainen pelaaja saisi 1–100-numeroisen kortin sijaan satunnaisluvun tasaisesti nollan ja yhden välille ja etsin pistettä x, jossa täydellinen loogikko ei välittäisi jäämisensä ja korttinsa vaihtamisen välillä. Tämän vastauksen avulla on helppo soveltaa vastausta diskreettiin jakaumaan välillä 1–100.
Lopetan puhumisen tähän ja annan lukijoideni nauttia ongelmasta. Katso vastaukset ja ratkaisut alla olevista linkeistä.
Vastaus jatkuvalle jakaumalle välillä 0 ja 1 .
Vastaus diskreetille jakaumalle välillä 1-100.
Ratkaisuni löydät napsauttamalla tästä (PDF) .
Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
Olettaen, ettei minkään hintaa tiedetä, mikä on optimaalinen strategia kilpailupelissä Hinta on oikea -teemassa?
Niille, jotka eivät tunne sääntöjä, pelaajalle annetaan neljä hintalappua, ja hänen on asetettava ne neljään esineeseen. Kun hän on valmis, hän vetää vivusta, joka antaa oikeiden osumien määrän. Jos pelaajalla on alle neljä oikein, hän voi järjestellä lappuja uudelleen ja yrittää uudelleen. Pelaaja voi yrittää niin monta kertaa kuin pystyy 45 sekunnin kuluessa.
Neuvoisin aina lähettämään valinnan, jolla on voittomahdollisuudet aiempien valintojen ja pisteiden perusteella. Jos ensimmäinen pistemäärä on 0, älä käännä kahta kahden tunnisteen sarjaa toisin päin, vaan siirrä kaikkea yhden pykälän verran jompaankumpaan suuntaan.
Jos et pysty suorittamaan logiikkaa heti, selitän sen sinulle alla. Käyttääksesi tätä strategiaa, anna eri tägeille kirjaimet A, B, C ja D. Aseta ne sitten näytetyssä järjestyksessä lavalla vasemmalta oikealle. Aloita aina ABCD:stä. Etsi sitten alla oleva partituurihistoria ja valitse kyseiselle partituurisekvenssille osoitettu tägien järjestys.
Jos 0, niin BCDA
Jos 0-0, niin CDAB
Jos 0-0-0, niin DABC (pakollinen voitto)
Jos 0–1, niin BDAC
Jos 0-1-0, niin CADB (pakollinen voitto)
Jos 0-1-1, niin CDBA
Jos 0-1-1-0, niin DCAB (täytyy voittaa)
Jos 0–2, niin BADC
Jos 0-2-0, niin DCBA (pakollinen voitto)
Jos 1, niin ACDB
Jos 1-0, niin BDCA
Jos 1-0-0, niin CABD
Jos 1-0-0-1, niin CBAC (pakollinen voitto)
Jos 1-1, niin BDCA
Jos 1-1-0, niin CABD
Jos 1-1-0-1, niin CBAC (pakollinen voitto)
Jos 1-1-1, niin BCAD (pakollinen voitto)
Jos 2, niin ABDC
Jos 2-0, niin BACD (pakollinen voitto)
Jos 2-1, niin ACBD
Jos 2-1-0, niin DBCA
Jos 2-1-1, niin ADCB
Jos 2-1-1-0, niin CBAD (täytyy voittaa)
Seuraava taulukko näyttää kunkin kokonaiskierrosten lukumäärän todennäköisyyden. Oikeassa alakulmassa oleva solu näyttää odotetun kierrosten lukumäärän 10/3.
Kilpailupeli
| Käännökset | Yhdistelmät | Todennäköisyys | Palata |
|---|---|---|---|
| 1 | 1 | 0,041667 | 0,041667 |
| 2 | 4 | 0,166667 | 0,333333 |
| 3 | 8 | 0,333333 | 1.000000 |
| 4 | 8 | 0,333333 | 1.333333 |
| 5 | 3 | 0,125000 | 0,625000 |
| Kokonais | 24 | 1.000000 | 3.333333 |
Tätä kysymystä käsitellään foorumillani Wizard of Vegasissa .
Mikä on todennäköisyys, että jokin pelaaja voittaa 25 000 dollaria Showcase Showdownissa Price is Right -pelissä?
Selityksenä muille lukijoille, haluan selittää, mistä puhut. Showcase Showdown on peli, jota pelataan The Price is Right -peliohjelmassa. Showcase Showdownissa jokainen pelaaja pyörittää vuorollaan kiekkoa, jolla on yhtä suuri todennäköisyys pysähtyä jokaiselle tasan 0,05:llä jaolliselle summalle välillä 0,05 - 1,00. Jos pelaaja ei pidä ensimmäisestä pyöräytyksestään, hän voi pyöräyttää uudelleen lisäämällä toisen pyöräytyksen ensimmäiseen, mutta jos hänen tuloksensa ylittää 1,00, hänet hylätään välittömästi. Tasapelin sattuessa jokainen pelaaja saa yhden pyöräytyksen tie-break-kierroksella, ja korkeimman pyöräytyksen saanut voittaa. Toisessa tasapelissä tämä prosessi toistuu, kunnes tasapeli on ratkaistu.
Showcase Showdownin päätarkoitus on edetä Showcaseen. Tarjolla on kuitenkin myös välittömiä käteispalkintoja, kuten:
- Jos pelaaja saa ensimmäisellä kierroksella yhteensä 1,00 dollaria, joko yhdellä summalla tai kahden pyöräytyksen summana, hän voittaa 1 000 dollaria.
- Jos ensimmäisessä ja ainoassa tie-break-kierroksessa pyörä pysähtyy 0,05 dollariin tai 0,15 dollariin, pelaaja voittaa 10 000 dollaria.
- Ensimmäisellä ja ainoalla tie-break-kierroksella, jos pyörä pysähtyy 1,00 dollariin, pelaaja voittaa 25 000 dollaria.
Selitän Showcase Showdownin optimaalisen strategian sarakkeessa 101. Olettaen, että tätä strategiaa noudatetaan, seuraava taulukko vastaa kysymyksiisi ja moniin muihin kysymyksiisi.
Showdownin tilastot
| Kysymys | Vastaus |
|---|---|
| Odotettu 1000 dollarin voittajien voitto ensimmäisellä kierroksella | 0,253790 |
| Todennäköisyys kahden pelaajan tasapeliin | 0.113854 |
| Todennäköisyys kolmen pelaajan tasapeliin | 0,004787 |
| Odotettu 10 000 dollarin voittajien toinen kierros | 0,024207 |
| Odotettu 25 000 dollarin voittajien voitto toisella kierroksella | 0.012104 |
| Odotettu palkintosumma yhteensä | 798,45 dollaria |
| Todennäköisyys sille, että jokin pelaaja voittaa 1000 dollaria | 0,084597 |
| Todennäköisyys sille, että jokin pelaaja voittaa 10 000 dollaria | 0,008069 |
| Todennäköisyys sille, että jokin pelaaja voittaa 25 000 dollaria | 0,004035 |
Taulukon alimmalla rivillä näkyy, että jos pääset Showcase Showdowniin ottamatta huomioon pyöräytystilaustasi, mahdollisuutesi voittaa 25 000 dollaria ovat 0,004035 eli 1/248.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Peliohjelmassa Survivor oli kaksi joukkuetta, toisessa yhdeksän pelaajaa ja toisessa kuusi. Heidät jaettiin sitten satunnaisesti kolmeen uuteen viiden hengen joukkueeseen. Jokaisessa uudessa joukkueessa oli kolme jäsentä entisestä yhdeksän pelaajan joukkueesta ja kaksi jäsentä entisestä kuuden pelaajan joukkueesta. Mitkä ovat tämän todennäköisyydet?
Kutsutaanpa ensin mainittua yhdeksän pelaajan joukkuetta joukkueeksi 1 ja kuuden pelaajan joukkuetta joukkueeksi 2. Joukkueesta 1 voidaan valita kolme pelaajaa ja joukkueesta 2 kaksi eri tapoja combin(9,3) × combin(6,2) = 1 260. Viiden pelaajan valitsemiseen 15 pelaajasta voidaan käyttää yhteensä combin(15,5) = 3 003 tapaa. Todennäköisyys sille, että ensimmäinen joukkue jakautuu 3/2 joukkueen 1 hyväksi, on siis 1 260/3 003 = 41,96 %.
Jos näin käy, joukkueella 1 on jäljellä kuusi pelaajaa ja joukkueella 2 neljä pelaajaa. Kolme pelaajaa joukkueesta 1 ja kaksi joukkueesta 2 voidaan valita combin(6,3)×combin(4,2) = 120. Viisi pelaajaa kymmenestä jäljellä olevasta pelaajasta voidaan valita yhteensä combin(10,5) = 252. Todennäköisyys sille, että toinen joukkue jaetaan 3/2 joukkueen 1 hyväksi, on 120/252 = 47,62 %, koska ensimmäinen joukkue on jo jaettu 3/2 tällä tavalla.
Jos kaksi ensimmäistä uutta joukkuetta jaetaan suhteessa 3/2 entisen joukkueen 1 hyväksi, viimeinen joukkue jaetaan suhteessa 3/2 jäljelle jääneiden kesken.
Näin ollen vastaus kysymykseesi on 41,96% × 47,62% × 100% = 19,98%.
Kaavat:
combin(x,y)=x!/((y!*(xy)!))
x! = 1*2*3*...*x
Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Mielestäni James Holzhauer hävisi tahallaan Emmalle viimeisessä pelissään. Todisteeni on, että hän oli panostanut isoja summia joka pelissä siihen asti, ja yhtäkkiä hän panostaa Emmaa vastaan vähän. Epäilen, että tuottajat haluavat Ken Jenningsin juontamaan ohjelmaa Alexin lähdettyä. Ohjelma olisi dramaattisempi, jos juontajalla olisi molempien ohjelmien tiedot ja voitetut rahat. Näin ollen he maksoivat Jamesille pelin pilaamisesta.
Anna kun avaan taustan. Kesäkuun 3. päivänä 2019 James oli lähellä rikkoa tavallisten pelien kokonaisvoittojen ennätyksen, joka on edelleen 2 520 700 dollaria. Jamesin keskimääräinen voitto per peli oli paljon enemmän kuin mitä hän tarvitsi ennätyksen rikkomiseen. Joten kaikki katseet olivat 3. kesäkuuta odottamassa ennätyksen rikkoutumista.
Sen sijaan James ei ainoastaan riko ennätystä, vaan häviää. Voittaja, Emma, pelasi erittäin vahvaa strategista peliä ja oli myös hyvä summerin kanssa ja vastasi oikein. Hän pelasi aivan kuten James normaalisti. Final Jeopardyyn mentäessä tulokset olivat:
- Emma – 26 600 dollaria
- James – 23 400 dollaria
- Jay – 11 000 dollaria
Näissä tilanteissa, joissa toisella sijalla on yli puolet ensimmäisestä sijasta ja kolmannella sijalla ei, tyypillisesti ensimmäinen ja toinen sijoittunut pelaaja valitsevat, kumpi panostus sitten on korkea tai matala. Korkea panos ensimmäiselle sijalle riittää varmistamaan voiton, jos se menee oikein. Tarkemmin sanottuna kaksi kertaa toisen sijan pisteet vähennettynä ensimmäisen sijan pisteillä plus yksi dollari. Juuri näin Emma teki panoksella 2 × 23 400 dollaria - 26 600 dollaria + 1 dollari = 20 201 dollaria. Useimmiten näin tekee ensimmäinen sijoittunut pelaaja.
James ei kuitenkaan tiennyt, mitä Emma tekisi päättäessään hänen panostaan. Seuraava taulukko näyttää kuka voittaisi milläkin panosyhdistelmällä.
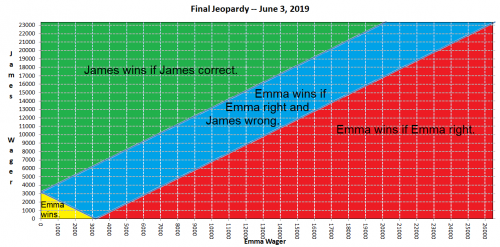
Klikkaa kuvaa nähdäksesi suuremman version.
Jos Emma panostaa vähintään 20 201 dollaria, hän lukitsee voiton, jos se menee oikein.
Jos Emma panostaa vähän, hän voittaa, jos joko (a) James panostaa vähän tai (b) James panostaa paljon ja on väärässä.
Jos James panostaa korkean panoksen, hän voittaa, jos (a) Emma panostaa korkean panoksen, Emma on väärässä ja James on oikeassa, tai (b) Emma panostaa matalan panoksen ja James on oikeassa.
Jos James panostaa vähän, hän voittaa, jos Emma panostaa paljon ja on väärässä.
Jos täydelliset loogikot pelaisivat, molemmat tekisivät päätöksensä satunnaisesti. Johtaja kuitenkin harvoin lyö matalaa korttia tilanteissa, joissa hänet voidaan saada kiinni. Jos James ennakoi Emman lyövän korkeaa korttia, hänen ehdottomasti pitäisi lyödä matalaa korttia. Tällä tavoin hänen ei tarvitse saada Final Jeopardya oikein voittaakseen, hänen tarvitsee vain toivoa, että Emma mokaa sen.
Jamesin todellinen tarjous oli oikea summa kattamaan Jayn panoksen, jos Jay panostaisi kaiken, ja se olisi oikeassa: 23 400 dollaria - 2 × 11 000 dollaria - 1 dollari = 1 399 dollaria, mikä tyydytti matalana panoksena Emman voittamista ajatellen.
Jos tulos on oikea, James saisi 1 000 dollaria lisää toiseksi tultuaan kolmanneksi.
Yhteenvetona totean, että hylkään täysin salaliittoteorian, jonka mukaan James heitti pelin pieleen. Hän pelasi oikein ja hävisi, koska pelasi vahvaa vastustajaa vastaan ja useimmat ihmiset kutsuvat sitä "huonoksi tuuriksi".
Ulkoiset linkit
- Jeopardyn kunniagalleria
- James Holzhauer Jeopardysta — Keskustelu foorumillani Wizard of Vegasissa.
Mikä on optimaalinen strategia Final Jeopardyssa, jos toiseksi sijoittuneella pelaajalla on yli 2/3 niin paljon rahaa kuin ensimmäiseksi sijoittuneella pelaajalla? Oleta, että kolmanneksi sijoittuneella pelaajalla ei ole merkitystä.
Haluaisin ensin tehdä pienen vastuuvapauslausekkeen. Seuraava analyysi perustuu tilastollisiin keskiarvoihin. Oikean pelaajan tulisi tehdä henkisiä muutoksia sen perusteella, kuinka hyvin hän tuntee Final Jeopardy -kategorian, sekä arvioida vastustajan mahdollisuuksia saada se oikein.
Vastatakseni kysymykseesi tarkastelin ensin Jeopardy Archiven neljän kauden dataa nähdäkseni neljä mahdollista yhdistelmää, joissa ensimmäinen (johtava) ja toinen (jahtaava) pelaaja saivat Final Jeopardin oikein ja väärin.
Jeopardy-tuloskortti
| Johtava pelaaja | Jahtaavaa pelaajaa oikein | Pelaajan jahtaaminen väärin | Kokonais |
|---|---|---|---|
| Korjata | 29,0 % | 25,5 % | 54,5 % |
| Väärä | 17,7 % | 27,8 % | 45,5 % |
| Kokonais | 46,8 % | 53,2 % | 100,0 % |
Ennen kuin jatkamme, määritellään joitakin muuttujia:
x = Todennäköisyys sille, että johtava pelaaja nousee korkealle.
y = Pelaajan perässä juoksemisen todennäköisyys on korkea.
f(x,y) = Korkeamman pistemäärän saaneen pelaajan voittotodennäköisyys.
Ilmaistaan f(x,y) yllä olevan taulukon x:n ja y:n avulla:
f(x,y) = 0,823xy + 0,545x(1-y) + 0,468(1-x)y + (1-x)(1-y)
f(x,y) = 0,810 xy - 0,455x - 0,532y + 1
Löytääksemme x:n ja y:n optimaaliset arvot, otetaan f(x,y):n derivaatta sekä x:n että y:n suhteen.
f(x,y) d/dx = -0,455 + 0,810y = 0
Näin ollen y = 0,455/0,810 = 0,562
f(x,y) d/dy = -0,532 + 0,810x = 0
Näin ollen x = 0,523/0,810 = 0,657
Joten korkean panoksen pelaajan tulisi panostaa korkealla todennäköisyydellä 65,7 % ja matalan panoksen pelaajan 56,2 %.
Katselukertojeni perusteella uskon, että korkean panoksen pelaajat panostavat korkeita summia yli 65,7 % ajasta, joten jos olisin toisella sijalla, valitsisin matalan panoksen.
Jos molemmat pelaajat noudattavat tätä satunnaistamisstrategiaa, todennäköisyys sille, että johtava pelaaja voittaa, on 70,1 %.
Jättäen kaiken teorian sikseen, jos olet johdossa, ennusta, mitä takaa-ajava pelaaja tekee, ja tee samoin. Jos olet takaa-ajamassa, ennusta johtavan pelaajan toiminta ja tee päinvastoin. Tämä strategia pätee kaikkiin tällaisiin turnauksiin.Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .
Miksi jotkut pelaajat, kuten James Holtzhauer, alkavat valita Jeopardy-kierroksen alussa alhaalta? Eikö olisi järkevämpää lämmitellä helpommilla kysymyksillä yläosassa, osittain varmistaakseen, että ymmärrys kategoriasta on oikea, koska ne ovat joskus hankalia?
Syynä on se, että päivittäiset tuplat sijoitetaan kolmelle alimmalle riville 91,5 % ajasta. Seuraava taulukko näyttää niiden sijainnit pelilaudalla yli 13 660 löydetyn päivittäisen tuplan perusteella.
Päivittäinen kaksoissijainti
| Rivi | Sarake 1 | Sarake 2 | Sarake 3 | Sarake 4 | Sarake 5 | Sarake 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 5 | - | 3 | 3 | 2 | 3 | 16 |
| 2 | 280 | 137 | 216 | 167 | 207 | 140 | 1 147 |
| 3 | 820 | 442 | 677 | 658 | 643 | 472 | 3 712 |
| 4 | 1 095 | 659 | 982 | 907 | 895 | 627 | 5 165 |
| 5 | 787 | 403 | 670 | 671 | 613 | 476 | 3 620 |
| Kokonais | 2 987 | 1 641 | 2 548 | 2 406 | 2 360 | 1 718 | 13 660 |
Lähde: J!-arkisto .
Tässä on sama data muodossa, kuinka usein päivittäinen tupla löytyy jokaisesta pelilaudan ruudusta.
Päivittäinen kaksinkertainen todennäköisyys
| Rivi | Sarake 1 | Sarake 2 | Sarake 3 | Sarake 4 | Sarake 5 | Sarake 6 | |
|---|---|---|---|---|---|---|---|
| 1 | 0,0 % | 0,0 % | 0,0 % | 0,0 % | 0,0 % | 0,0 % | 0,1 % |
| 2 | 2,0 % | 1,0 % | 1,6 % | 1,2 % | 1,5 % | 1,0 % | 8,4 % |
| 3 | 6,0 % | 3,2 % | 5,0 % | 4,8 % | 4,7 % | 3,5 % | 27,2 % |
| 4 | 8,0 % | 4,8 % | 7,2 % | 6,6 % | 6,6 % | 4,6 % | 37,8 % |
| 5 | 5,8 % | 3,0 % | 4,9 % | 4,9 % | 4,5 % | 3,5 % | 26,5 % |
| Kokonais | 21,9 % | 12,0 % | 18,7 % | 17,6 % | 17,3 % | 12,6 % | 100,0 % |
Päivittäisten tuplausten etsimisen syy on se, että ne ovat hyvä tapa tuplata pisteet. Useimmilla kilpailijoilla on noin 80–90 %:n todennäköisyys saada mikä tahansa vihje oikein. On erittäin arvokasta saada tasarahat vedosta, jolla on 80–90 %:n voittomahdollisuus. Tärkein syy siihen, miksi James Holtzhauer voitti niin paljon kuin voitti, oli aggressiivinen päivittäisten tuplausten etsintä ja sitten all-in suurimman osan ajasta, kun hän löysi ne. Näin hän myös hävisi Emmalle, kun tämä käytti samaa strategiaa häntä vastaan.
Mikä on paras strategia pelata kilpailupeliä "hinta on oikea" -periaatteella, olettaen, että pelaajalla ei ole aavistustakaan palkintojen hinnoista?
Niille lukijoille, jotka eivät tunne peliä, tässä on video siitä.
Väitän, että seuraava strategia johtaa keskimääräiseen vähimmäismäärään käännöksiä. On monia strategioita, jotka tasoittaisivat sen, mutta en usko, että mikään voi voittaa sitä.
Käyttääksesi strategiaa, merkitse neljä hintalappua numeroilla 1, 2, 3 ja 4. Aseta ne neljälle palkinnolle sen mukaan, kuinka monta olet aiemmin saanut oikein, aloittaen ensimmäisestä käännöksestä vasemmalla.
Kilpailupelistrategia
| Historia | Palkinto 1 | Palkinto 2 | Palkinto 3 | Palkinto 4 |
|---|---|---|---|---|
| Ei mitään | 1 | 2 | 3 | 4 |
| 0 | 2 | 1 | 4 | 3 |
| 0,0 | 3 | 4 | 2 | 1 |
| 0,0,0 | 4 | 3 | 1 | 2 |
| 0,0,2 | 3 | 4 | 1 | 2 |
| 0,0,2,0 | 4 | 3 | 2 | 1 |
| 0,2 | 2 | 3 | 4 | 1 |
| 0,2,0 | 4 | 1 | 2 | 3 |
| 0,2,1 | 2 | 4 | 1 | 3 |
| 0,2,1,0 | 3 | 1 | 4 | 2 |
| 1 | 1 | 3 | 4 | 2 |
| 1,0 | 2 | 4 | 3 | 1 |
| 1,0,0 | 3 | 1 | 2 | 4 |
| 1,0,0,0 | 4 | 2 | 1 | 3 |
| 1,1 | 1 | 4 | 2 | 3 |
| 1,1,0 | 2 | 3 | 1 | 4 |
| 1,1,0,0 | 3 | 2 | 4 | 1 |
| 1,1,0,0,0 | 4 | 1 | 3 | 2 |
| 2 | 2 | 1 | 3 | 4 |
| 2,0 | 1 | 2 | 4 | 3 |
| 2,1 | 1 | 3 | 2 | 4 |
| 2,1,0 | 4 | 2 | 3 | 1 |
| 2,1,1 | 1 | 4 | 3 | 2 |
| 2,1,1,0 | 3 | 2 | 1 | 4 |
Seuraava taulukko näyttää todennäköisyyden, että neljän hintalapun järjestämiseen tarvitaan 1–5 kierrosta 24 mahdollisesta tavasta.
Vaaditut käännökset
| Käännökset | Määrä | Todennäköisyys |
|---|---|---|
| 1 | 1 | 4,17 % |
| 2 | 4 | 16,67 % |
| 3 | 8 | 33,33 % |
| 4 | 9 | 37,50 % |
| 5 | 2 | 8,33 % |
| Kokonais | 24 | 100,00 % |
Pistetulon perusteella keskimääräinen tarvittavien kierrosten lukumäärä tässä strategiassa on 3,29167.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Kuulin jotain kahden kolmasosan säännöstä Final Jeopardy -vedonlyönnissä. Tiedätkö siitä?
Kyllä. Se viittaa kakkospelaajan strategian muutokseen, jos hänellä on yli 2/3 ensimmäisen pelaajan pisteistä.
Yksinkertaistetaan tilanne kahden pelaajan peliksi seuraavasti:
- Tilanne A: Toisella sijalla on alle puolet ensimmäisestä sijasta.
- Tilanne B: Toisella pelaajalla on 1/2–2/3 ensimmäisestä sijasta.
- Tilanne C: Toisella sijalla on yli 2/3 ensimmäisestä sijasta.
Ennen kuin jatkan, haluan muistuttaa lukijaa Jeopardy-sääntömuutoksesta, joka koskee tasapelejä viimeisen Jeopardin jälkeen. Molemmat pelaajat eivät enää etene, mutta nyt on olemassa äkkikuolema-kysymys tie-breakissa. Tässä on tällainen tilanne .
Tilanne A
Olkoon A = 10 000 dollaria ja B = 4 000 dollaria
Pelaajan A ei tulisi ottaa riskiä häviämisestä panostamalla enintään A-2B-1. Jos hän ei ole varma kategoriassa, hän voi panostaa 0 dollaria. Kummassakin tapauksessa hän varmistaa voiton. Tässä tapauksessa A:n tulisi panostaa 0–1 999 dollaria.
Pelaajalla B ei ole toivoa, ellei A panosta liikaa ja epäonnistu. Tässä tapauksessa B:n tulisi ottaa huomioon kolmannen sijan tulos ja yrittää pysyä sitä korkeammalla, jos mahdollista, voittamalla toisesta sijasta 2 000 dollaria kolmannen sijan 1 000 dollarin sijaan.
Tilanne B
Olkoon A = 10 000 dollaria ja B = 6 000 dollaria
A:n strategia on odottaa B:n panostavan kaiken ja panostaa tarpeeksi kattaakseen 2B:n, jos vastaus on oikea. Varmuuden vuoksi hänen ei kuitenkaan tulisi panostaa liikaa, jotta hän ei putoa B:n alapuolelle, jos vastaus on väärä. Tässä tapauksessa hänen tulisi panostaa vähintään 2B-A+1 ja AB-1. Tässä tapauksessa vaihteluväli on 2 001–3 999 dollaria.
B:n strategiana on saada ainakin tarpeeksi pisteitään ohittaakseen A:n, jos vastaus on oikein, ja parantaakseen kokonaispisteitään. Tässä tapauksessa 4 001 ja 6 000 dollaria.
Jos molemmat pelaajat toimivat odotetusti ja noudattavat tätä strategiaa, pelaaja B voi voittaa vain, jos A on väärässä ja B on oikeassa. Tämän todennäköisyys on noin 19 %.
Tilanne C
Tässä asiat monimutkaistuvat ja niihin liittyy enemmän peliteoriaa ja satunnaistamista.
Olkoon A = 10 000 dollaria ja B = 7 000 dollaria.
Ennen kuin jatkamme, on tärkeää arvioida todennäköisyys sille, että Final Jeopardy -vihje vastattiin oikein. Kausien 30–34 perusteella ensimmäinen pelaaja oli oikein 52 % ajasta ja toinen 46 %. Nämä todennäköisyydet ovat kuitenkin positiivisesti korreloituneita. Tässä on erittely kaikista neljästä mahdollisuudesta:
- Molemmat oikein: 27%
- Ensimmäinen sija oikein, toinen sija väärin: 25%
- Ensimmäinen sija väärin, toinen sija oikein: 19%
- Molemmat väärin 29%.
Vaikka kahden ensimmäisen pelaajan Jeopardy-keskiarvo on 49 %, todennäköisyys sille, että molemmat ovat oikeassa tai väärässä, on 56 %.
Nämä voivat tietenkin muuttua kategorian mukaan, mutta pidetään asiat yksinkertaisina ja käytetään yllä olevia todennäköisyyksiä.
Tässä tilanteessa pelaajan B ei tarvitse olla riippuvainen siitä, että A on väärässä ja B oikeassa. Hän voi panostaa vähän, esimerkiksi 0 dollaria, varmistaen voiton, jos A on väärässä. Toisin sanoen, jos A panostaa tarpeeksi kattaakseen B:n, jos tämä on oikeassa, hän voi pudottaa B:n panoksen alle, jos hän on väärässä, ja B panostaa 0 dollaria.
Jos A kuitenkin ennusti B:n panostavan matalan summan, esimerkiksi 0 dollaria, niin A voisi lukita voiton panostamalla myös 0 dollaria. Molemmilla pelaajilla on periaatteessa valinnanvaraa, panostavatko he matalaan vai korkeaan summaan. A:n tulisi haluta panostaa samalla tavalla kuin B ja B:n tulisi haluta panostaa päinvastaisella tavalla kuin B. Jos molemmat pelaajat olisivat täydellisiä loogikoita, he tekisivät päätöksensä satunnaisesti.
Tässä tapauksessa A:n korkean panoksen tulisi olla 2B-A+1 vs. AB-1, sama kuin tilanteessa B. Tässä tapauksessa 2 999 dollaria ja 4 001 dollaria. A:n matalan panoksen tulisi olla 0 dollaria.
B:n korkean panoksen tulisi olla sama kuin tilanteessa B, panosta riittävästi läpäistäksesi A:n, jos se oikein on. Tässä tapauksessa 3 001 dollaria ja 7 000 dollaria. B:n matalan panoksen tulisi olla 0 dollaria.
Anteeksi, jos ohitan matematiikan ja siirryn suoraan molempien pelaajien satunnaistamisstrategioihin.
Pelaajan A tulisi valita korkea todennäköisyys 62,3 % ja matala todennäköisyys 37,7 %.
Pelaajan B todennäköisyyden tulisi olla korkea 61,2 % ja todennäköisyyden matala 38,8 %.
Olettaen, että molemmat pelaajat noudattavat tätä satunnaistamisstrategiaa ja yllä mainitut todennäköisyysparit ovat oikein, pelaajan A voittotodennäköisyys on 65,2 %.
Jos pelaajalla A olisi yli 2/3 pelaajan B pisteistä, hänen voittotodennäköisyytensä nousisi 81,0 prosenttiin.
Molempien pelaajien tulisi pitää mielessä 2/3-säännön merkitys lyödessään vetoa Double Jeopardy -pelistä.