WOO logo

Velho suosittelee

Todennäköisyys - Yleisiä kysymyksiä

Tarkoitatko, että pitkällä aikavälillä häviät jokaisessa kasinopelissä, teetpä mitä tahansa?

Joe alkaen Harrisburg, US

Harvinaisia positiivisen odotuksen mahdollisuuksia blackjackissa ja videopokerissa lukuun ottamatta, kyllä, juuri sitä tarkoitan.

Miten voin muuntaa todennäköisyytesi x-y-muotoon?

Ralph Harpster alkaen Turlock, USA

Sanomalla, että jonkin tapahtuman todennäköisyys on x:y, tarkoitetaan, että kyseinen tapahtuma tapahtuu x kertaa jokaista y kertaa kohden, kun se ei tapahdu. Muunnoksen tekemiseksi olkoon p jonkin tapahtuman todennäköisyys. Todennäköisyys voidaan ilmaista myös muodossa (1/p)-1:1. Katsotaanpa esimerkkiä. Täyskäden saamisen todennäköisyys viiden kortin avopokerissa on 0,00144058. Tämä voidaan esittää myös muodossa 693,165:1.

Katselin hiljattain käynnissä olevaa jalkapallovetoa. Se oli sellainen, jossa ruudukossa oli 100 ruutua ja numerot 0-9 kulkivat X- ja Y-akseleilla ja vastaavat tuloksen viimeistä numeroa. En ole jalkapallofani enkä lyönyt vetoa tästä vedosta, mutta olen uhkapeluri enkä pidä sitä kovin hyvänä vetona.

Oletan, että tiedät minkä tyyppiseen pooliin viittaan. Jokainen laatikko maksaa 5 dollaria ja voitot maksetaan neljännesvuosittain. Jos laatikkosi voittaa, voitat 125 dollaria, ja on mahdollista voittaa kaikki neljä neljännestä, jos viimeiset numerot pysyvät samoina, jolloin voitat 500 dollaria, jolloin voittokerroin on 100:1.

Vedonlyöjä yritti kertoa minulle, että 500 dollarin voittotodennäköisyys on 100:1. Olen eri mieltä. Ensinnäkin laatikolla, jossa on 0 + 7, on paljon paremmat mahdollisuudet voittaa kuin laatikolla, jossa on 2 + 9. Todennäköisyys sille, että pelin kahdeksi viimeiseksi numeroksi jää 0 + 7, on kuitenkin korkea. Jos laatikot valitaan sinulle satunnaisesti, voitko kertoa minulle likimääräiset todennäköisyydet voittaa 500 dollarin palkinto?

Sam alkaen Phillipsburg, USA

Olettaen, että ruudukon solut valitaan satunnaisesti, minkä tahansa neljänneksen voittotodennäköisyys olisi 1/100. Olettaen, että jokainen neljännes olisi itsenäinen tapahtuma, mitä ne eivät ole, kaikkien neljän neljänneksen voittotodennäköisyys olisi (1/100) 4 = 1 sadasta miljoonasta.

Haluaisin todella tietää, miten kertoimia, kuten 12:1 tai 3:2, luetaan. Kumpi näyttää parhaat voittomahdollisuudet? 12:1 vai 3:2?

Louis alkaen Montreal, Canada

En pidä todennäköisyyksien käyttämisestä tuossa muodossa, mutta niitä käytetään yleensä tällaisessa syntaksissa: "Kuningasvärisuoran saamisen todennäköisyys on 649 739:1." Tämä tarkoittaa, että on 649 739 tapaa, joilla kuningasvärisuoraa ei voi saada, ja yksi tapa, jolla sen voi saada. Esimerkeissäsi 12:1 on todennäköisyys 1/13 eli 7,69 %, ja 3:2 on 2/5 eli 40,00 %, joten 3:2 on parempi mahdollisuus voittaa.

St. Louis Post-Dispatch -lehden artikkelissa toimittaja sanoo: "500 vuoden välein tapahtuva tulva on sellainen, jonka todennäköisyys tapahtua tiettynä vuonna on 1/500. Toisin sanoen, sen todennäköisyys olisi 1/10 50 vuoden aikana tai 1/5 vuosisadan aikana." Luettuani kaikki uhkapelisivunne uskon, että tämä ei ole oikea tapa ilmaista asia, eihän? Heidän väitteensä ekstrapoloimalla se tarkoittaisi, että tulvan todennäköisyys on 1/1 500 vuoden välein, eikä se voi mitenkään pitää paikkaansa.

anonyymi

Olet oikeassa, tuo artikkeli on virheellinen. 500 vuoden välein tapahtuvan tulvan todennäköisyys x vuoden aikana on 1-e -x/500 . Joten ainakin yhden 500 vuoden välein tapahtuvan tulvan todennäköisyys 50 vuodessa on 9,52 % ja 100 vuodessa 18,13 %.

Jos määritän pelin reilun linjan olevan -160/+160 ja löydän väärän linjan olevan -145, mikä on EV:ni? Olisin erittäin tervetullutta, jos voisitte antaa kaavan, jolla voisin johtaa EV:ni +/- reilun linjan määrittämisen jälkeen.

anonyymi

Olkoon p suosikin voittotodennäköisyys. Jos -160 on reilu jako, niin:

100*p - 160*(1-p) = 0
260p = 160
p = 160/260 = 8/13 = 61,54 %.

Joten odotettu tuotto 145 dollarin panokselle -145 kertoimella olisi (8/13)*100 + (5/13)*-145 = 75/13 = 5,77 dollaria. Pelaajan etu olisi siis 5,77 dollaria/145 dollaria = 3,98 %.

Määritellään t todelliseksi voittolinjaksi ilman talon etua ja a varsinaiseksi voittolinjaksi. Seuraavat ovat kaavat pelaajan odotetulle tuotolle:

A on negatiivinen, t on negatiivinen: (100*(ta) / (a*(100-t))
A on positiivinen, t on positiivinen: (at)/(100+t)
A on positiivinen, t on negatiivinen: (a*t + 10000)/((t-100)*100)

Joten sinun tapauksessasi odotettu tuotto on 100*(-160 -(-145))/(-145*(100-(-160))) = 3,98 %.

Mitä mieltä olet alla olevasta väitteestä, jonka mukaan Jumala on demokraatti, kuten osoittaa se tosiasia, että kaikki piirikunnat, jotka äänestivät Goren puolesta vuonna 2000, säästyivät Floridaan hiljattain iskeneiltä kolmelta hurrikaanilta?

anonyymi

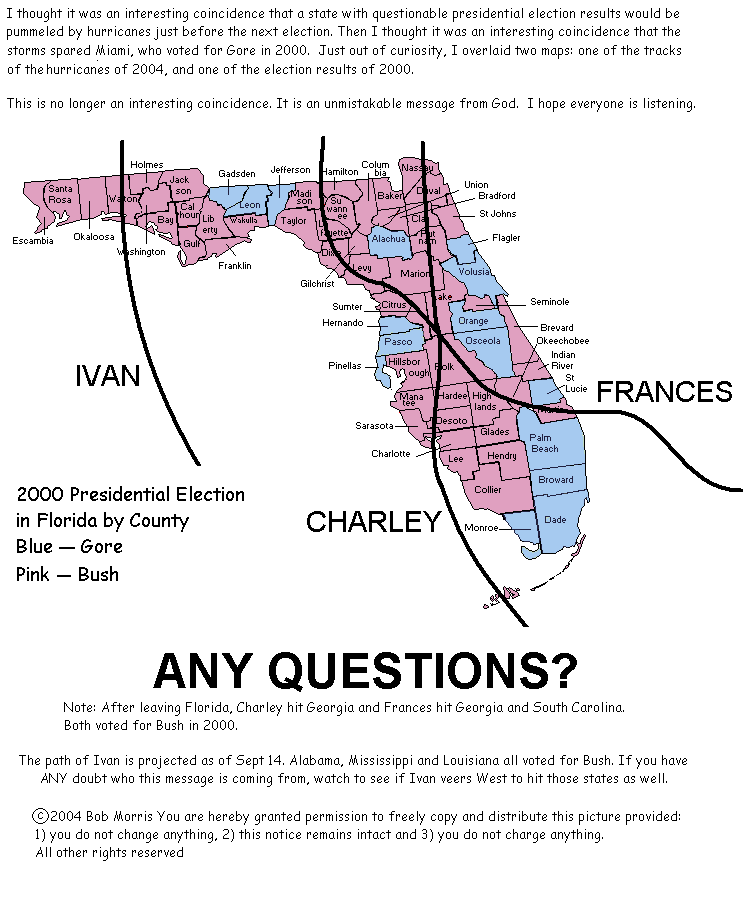
Ensinnäkin julkaisen tämän, koska kirjoittaja antaa siihen luvan tekstin lopussa. Tämä on hyvä esimerkki siitä, että korrelaatio ei välttämättä tarkoita syy-seuraussuhdetta. On helppo katsoa ajassa taaksepäin ja löytää paljon yhteensattumia. Jotta jokin asia voidaan perustella, hypoteesi tulisi esittää ennen todisteiden keräämistä.

Jatkoa (13. marraskuuta 2004): Eräs toinen lukija huomautti, että tämä kartta alkoi vitsinä, mutta siitä tulikin urbaanilegenda . Kuten tämä linkki osoittaa, grafiikan hurrikaanien reitit eivät yksinkertaisesti olleet tarkkoja ja todelliset hurrikaanit iskivät moniin Goren piirikuntiin. Se vain osoittaa, ettei kaikkea luettua kannata uskoa, etenkään internetissä.

Ajattelin vain, että tämä voisi kiinnostaa sinua. Bodog tarjoaa seuraavan vedon: "Onko Britney Spearsin ja Kevin Federlinen toinen lapsi poika vai tyttö?" Pojan kertoimet ovat +105 ja tytön kertoimet −145. Viimeksi kun tarkistin, tämä on ollut 1:1 ihmiskunnan alusta lähtien. Haluaisin tietää, kuka on tässä vedossa -145:n puolella. Tykkää sivustosta, käy siellä usein ja klikkaa sponsoreitasi kiitollisuuden osoituksena.

anonyymi

Kiitos ystävällisistä sanoista. Rehellisesti sanottuna kukaan ei enää välitä klikkausprosenteista. Joten älä tunne velvollisuutta klikata bannereita, jos se on vain näön vuoksi. Vastauksena kysymykseesi, Yhdysvalloissa todennäköisyydet ovat hyvin lähellä 50,5 % poikien ja 49,5 % tyttöjen kohdalla. Olettaen, että vedonlyöntiyhteisöllä ei ole muuta tietoa, pelaajan etu pojan vedossa olisi 0,505 * 1,05 - 0,495 = 3,53 %. Voisi olla, että joku sisäpiirin tietoa omaava henkilö lyö vetoa tytöstä. Toinen teoria on, että jotkut ihmiset uskovat virheellisesti, että sukupuoli voidaan päätellä äidin vatsan muodosta, ja nämä ihmiset lyövät vetoa tytöstä. Henkilökohtaisesti jätän tämän sikseen.

Tässä YouTube-videossa Matt Damon sanoo, että John McCainilla on 1/3 mahdollisuus olla selviämättä ensimmäisestä kaudestaan. Onko hän oikeassa?

Lisa alkaen San Antonio, TX

Ei. Käyttämällä tätä CDC:n (Centers for Disease Control) vakuutusmatemaattista taulukkoa , 72-vuotiaan valkoihoisen miehen todennäköisyys selvitä 76-vuotiaaksi on 85,63 %. Se on noin 1/7 kuoleman mahdollisuus. Eloonjäämisaste voidaan löytää jakamalla 76-vuotiaana syntyneiden kohortin luku 57 985 luvulla 72-vuotiaana syntyneiden kohortin luku 67 719 luvulla valkoisten miesten taulukosta sivulla 14. Käytetty taulukko on nimeltään "jakson elinaikataulukko", jossa oletetaan, että vuoden 2003 kuolleisuusasteet eivät muutu tulevaisuudessa, ja se on yleisimmin käytetty vakuutusmatemaattinen taulukko. Perfektionisti saattaisi haluta käyttää vuoden 1936 kohortin elinaikataulukkoa, mutta en usko, että sillä olisi paljon merkitystä.

ps Lähetettyäni tämän vastauksen olen saanut useita kommentteja, joiden mukaan vastaukseni ei ottanut huomioon John McCainin yksilöllistä terveydentilaa. Häntä vastaan työskentely on kuin syöpästä selviytyminen. Hänen edukseen toimii pääsy parhaaseen mahdolliseen lääketieteelliseen hoitoon, jonka rahalla saa, hän on selvästi edelleen hyvässä henkisessä ja fyysisessä kunnossa 72-vuotiaaksi, ja hänellä on pitkä elinikä, mistä on osoituksena se, että hänen äitinsä on edelleen elossa. En kuitenkaan koskaan tarkoittanut ottaa tätä tietoa huomioon. Matt Damon lainasi vakuutusmatemaattisia taulukoita, joihin viittasin. Sanon vain, että keskimääräisen 72-vuotiaan valkoisen miehen todennäköisyys selviytyä neljä vuotta lisää on 86%. Jos pakotetaan, ennustaisin John McCainin todennäköisyyksien olevan vielä paremmat.

Jos paperia on yhtä paljon, kumpi paperikuppi pitäisi enemmän vettä, sylinterin vai kartion muotoinen? Oletetaan, että sylinteri on avoin toisesta päästä ja että molemmissa tapauksissa mitat ovat optimaaliset.

anonyymi

Vastauksen ja ratkaisun löydät kumppanisivustoltani MathProblems.info , tehtävästä numero 210.

Oletko kuullut tarinan Princessistä, New Jerseyn Popcorn Parkin eläintarhan kamelista, jonka NFL-otteluiden tasoitusten saldo on 88–51? Mitkä ovat sen todennäköisyydet?

anonyymi

Laskematta pois lyötyjä vetoja, todennäköisyys saada vähintään 88 voittoa 139 valinnasta on 0,00107355 eli 1/931. Tämä on melko pettymys. Olen varma, että on olemassa 930 muuta eläintä, jotka pärjäsivät huonommin, mutta joista kukaan ei kirjoita. Lisätietoja Princessistä saat lukemalla artikkelin NJ camel predicts Giantsin voittavan Patriotsin ESPN.comissa.

Chelsea sanoi 8. toukokuuta 2012 Chelsea Lately -ohjelmassa, että punatukkaiset kuolevat sukupuuttoon, koska ne eivät pariudu keskenään. Onko tämä totta?

anonyymi

Toivottavasti olet tyytyväinen; käytin tähän tuntikausia.

Vastatakseen kysymykseen on tärkeää mitata käyttäytymistä Chelsea Handlerin punapäähypoteesin mukaisesti. Tässä ovat oletukseni.

  1. Punapää ei koskaan pariudu toisen punapään kanssa.
  2. Naaras valitsee aina uroksen, jonka kanssa paritella.
  3. Kaikki parittelevat ja jokainen parittelu tuottaa saman määrän lapsia.
  4. Punatukkaiset naaraspuoliset saavat ensimmäiset dibit kaverin luona valitsemalla satunnaisesti ei-punapäisten joukosta.
  5. Naaraspuoliset kantajat (joilla on yksi punahiuksisuuden geeni) valitsevat kumppanin satunnaisesti punapäiden jäljelle jääneiden miesten joukosta.
  6. Negatiiviset naiset (joilla ei ole punatukkaisuusgeeniä) valitsevat satunnaisesti punapäisten ja kantajien jäljelle jääneiden miesten joukosta.

Aloitan punahiuksisuuden todennäköisyydellä 4 % Today I Found It -sivuston mukaan. Oletan sitten, että ennen tätä ei ollut ennakkoluuloja punapäitä kohtaan.

Olettaen, että punapäisyyteen kohdistuva ennakkoasenne alkaa seuraavasta sukupolvesta ja jatkuu, mikä on punahiusten määrän kasvu koko väestössä? Paljon taulukkolaskentaohjelman avulla tehdyn työn jälkeen, johon en mene tässä tarkemmin, tässä ovat kahdeksan ensimmäistä sukupolvea tästä alkaen.

Punaisten hiusten osuus

Sukupolvi Osuus
1 4,000000 %
2 3,888889 %
3 3,895219 %
4 3,894863 %
5 3,894883 %
6 3,894882 %
7 3,894882 %
8 3,894882 %

Näemme, että kolmanteen sukupolveen mennessä punatukkaisten osuus väestöstä lähenee 3,90 prosenttia. Joten huolimatta siitä, mitä Chelsea saattaa sanoa, mielestäni punapäillä ei ole mitään hätää.

Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
CardPlayer.comin mukaan Amir Lehavot, yksi yhdeksästä pelaajasta, jotka pääsivät World Series of Pokerin finaalipöytään vuonna 2013, myy kaikki yhdeksännen sijan vähimmäispanoksen 733 224 dollaria ylittävät voitot hintaan 29 248 dollaria jokaista 1 %:n osuutta kohden. Onko tämä kohtuullinen hinta?

anonyymi

Tarkastellaan ensin pelimerkkipinoja.

Vuoden 2013 WSOP:n finaalipöydän pelimerkkipinot

Pelaaja Sipsit
JC Tran 38 000 000
Amir Lehavot 29 700 000
Marc McLaughlin 26 525 000
Jay Farber 25 975 000
Ryan Riess 25 875 000
Sylvain Loosli 19 600 000
Michiel Brummelhuis 11 275 000
Mark Newhouse 7 350 000
David Benefield 6 375 000

Seuraava taulukko näyttää turnauksen kunkin lopputuloksen voiton.

Vuoden 2013 WSOP:n finaalipöydän palkintorahat

Paikka Voittaa
1. 8 359 531 dollaria
2. sija 5 173 170 dollaria
3. sija 3 727 023 dollaria
4. 2 791 983 dollaria
5. päivä 2 106 526 dollaria
6. päivä 1 600 792 dollaria
7. päivä 1 225 224 dollaria
8. päivä 944 593 dollaria
9. päivä 733 224 dollaria

Olettaen, että jokaisella pelaajalla on sama taitotaso, voiton todennäköisyys voitaisiin arvioida osuutena kokonaispelimerkeistä. Asia kuitenkin monimutkaistuu jokaisella pelimerkillä sen jälkeen. Kysymykseen vastaamiseksi kehitin pokeriturnauslaskurini .

Syötettyäsi yllä olevat tiedot näet, että Amirin odotettu voitto on 3 658 046 dollaria. Vähennä sitten 9. sijan vähimmäispalkinto 733 224 dollaria, jolloin saat odotettuina takaamattomina voittoina 2 924 822 dollaria. Jokaisen 1 %:n osuuden arvo on 29 248,22 dollaria. Tämä on kätevästi cardplayer.com-artikkelissa mainittu hinta.

Muuten, Lehavot sijoittui kolmanneksi ja voitti 3 727 023 dollaria palkintorahaa. Kun yhdeksännen sijan 733 224 dollarin takuupotti vähennettiin ja jaettiin sadalla, saatiin jokainen 1 %:n osuus, joka tuotti 29 938 dollaria. Alkuperäinen osakekohtainen hinta oli 29 248 dollaria, joten jokainen osake olisi tuottanut 2,36 %:n voiton.

Tätä kysymystä käsitellään foorumillani Wizard of Vegasissa .

Kasinokampanjoissa, joissa käytetään edelleen tavallisia lippuja oikeassa rummussa (eikä sähköisissä), joissa lippusi tulostetaan pelaajan tiskillä ja laitetaan rumpuun – taivutetaanko/rypistetäänkö lippuja ennen niiden laittamista rumpuun? Luuletko, että taivutetuilla lipuilla on paremmat mahdollisuudet tulla valituiksi?

AxiomOfChoice

Toivottavasti olet tyytyväinen. Vastatakseni tähän kysymykseen ostin Office Depotista ison rullan lippuja. Sitten laitoin 500 lippua paperipussiin, taittelin ne puoliksi noin 90 asteen kulmassa ja avasin toisen puolen. Sitten pyysin kuutta vapaaehtoista nostamaan kukin 40–60 lippua yksi kerrallaan ja lisäämään uuden laatikon, samalla kun kirjasin tulokset muistiin. Tässä ovat tulokset.

Lippujen arvontakokeilu

Aihe Taitettu Avattu Kokonais
1 25 25 50
2 38 22 60
3 25 15 40
4 34 16 50
5 27 23 50
6 26 24 50
Kokonais 175 125 300


Joten 58,3 % arvotuista lipuista taitettiin!

Jos oletetaan, että luovuttamisella ei ollut vaikutusta, tulokset olisivat 2,89 keskihajonnan päässä odotuksista. Todennäköisyys saada näin monta tai enemmän luovutettua lippua, olettaen, että luovuttaminen ei vaikuttanut kertoimiin, on 0,19 % eli 1/514.

Voisin lisätä, että kiireesti arpoja nostaneet koehenkilöt nostivat paljon todennäköisemmin taitettuja arpoja. Ne, jotka ottivat jokaisen arvon huolellisesti ja ajoissa, olivat lähellä tai 50/50-jakaumaa.

Joten johtopäätökseni on ehdottomasti luovuttaa.

Keskustellaksesi tästä kysymyksestä, käy foorumillani Wizard of Vegasissa .

Kahdelle pelaajalle jaetaan kullekin satunnainen luku (0,1)-kohdassa. Ensimmäinen pelaaja päättää joko jäädä odottamaan tai hylätä ja nostaa uuden numeron. Toinen pelaaja tekee samoin. Suuri numero voittaa. Mikä on optimaalinen strategia kummallekin pelaajalle? Olettaen optimaalisen strategian, mikä on todennäköisyys, että kukin pelaaja voittaa?

Joe Shipman alkaen New Jersey

Hyvä kysymys! Tässä on vastaukseni ja pintapuolinen ratkaisuni . Katso myös ratkaisuni PDF-muodossa .

Oletetaan, että sinulle tarjotaan mahdollisuutta pelata kolikonheittopeliä. Jos ensimmäinen heitto on kruuna, saat takaisin 2 dollaria ja peli on ohi. Muussa tapauksessa käännät kortin uudelleen. Jos toinenkin heitto on kruuna, saat takaisin 4 dollaria. Jos toinenkin heitto on klaava, jatkat kolikonheittoa, kunnes saat kruunan. Jokaisella heitolla palkinto kaksinkertaistuu. Toisin sanoen saat takaisin 2^n, jossa n on heittojen lukumäärä (mukaan lukien viimeinen kruunaheitto). Kuinka paljon maksaisit tästä pelistä? Olen kuullut, että matemaattinen vastaus on ääretön määrä rahaa, mutta tämä ei ole järkevää, koska sinun on voitettava äärellinen määrä rahaa jossain vaiheessa.

Omaha

Tämä tunnetaan nimellä Pietarin paradoksi .

On totta, että pelin odotettu voitto on ∞, mutta samaan aikaan todennäköisyys sille, että kolikko lopulta pysähtyy hännälle, johtaa rajalliseen rahasummaan. Odotetun voiton laskeminen on:

Odotettu voitto = pr(1 voltti)×2 + pr(2 volttia)×4 + pr(3 volttia)×8 + pr(4 volttia)×16 + pr(5 volttia)×32 + pr(6 volttia)×64 + ... =

(1/2) 1 × 2 1 + (1/2) 2 × 2 2 + (1/2) 3 × 2 3 + (1/2) 4 × 2 4 + (1/2) 5 × 2 5 + (1/2) 6 × 2 6 + ...

= ((1/2)*(2/1)) 1 + ((1/2)*(2/1)) 2 + ((1/2)*(2/1)) 3 + ((1/2)*(2/1)) 4 + ((1/2)*(2/1)) 5 + ((1/2)*(2/1)) 6 + ...

= 1 1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + ...

= 1 + 1 + 1 + 1 + 1 + 1 + 1 + ... = ∞

Paradoksaalista tässä on se, että pelaajan on voitettava rajallinen määrä rahaa, mutta odotettu voitto on ääretön. Miten se voi olla mahdollista?

Tämä ei luultavasti ole kovin tyydyttävä vastaus, mutta ∞:hen liittyy paljon paradokseja. Tämä saattaa aiheuttaa minulle vihaisia sähköposteja, mutta se, mikä antaa minulle mahdollisuuden nukkua öisin näistä äärettömyyden paradokseista huolimatta, on se, että uskon ∞:n olevan matemaattinen tai filosofinen käsite, jonka olemassaoloa todellisessa fyysisessä maailmankaikkeudessa ei ole todistettu. Tämä äärettömyyden käsite tai teoria tuo mukanaan sisäänrakennettuja paradokseja.

Niille, jotka ovat eri mieltä tästä, kertokaa minulle jotain, jolla on todistetusti ääretön määrä tai mitta. Älkää väittäkö, että mustalla aukolla on ääretön tiheys, ellette ole todisteita sen koosta.

Vastataksemme alkuperäiseen kysymykseen siitä, kuinka paljon pelin pelaamisesta pitäisi maksaa, meidän on pidettävä mielessä, että onnellisuus ei ole verrannollinen rahan määrään. Minulle henkilökohtaisesti opetettiin taloustieteen tunneilla, ja uskon, että rahan hyöty eli onnellisuus on verrannollinen rahan määrän logaritmiin. Tämän oletuksen mukaan, jos kahden ihmisen varallisuutta lisätään tai vähennetään samalla prosenttiosuudella, lukuun ottamatta alkuperäistä nollavaraisuutta, he molemmat kokevat saman onnellisuuden muutoksen. Esimerkiksi jos Jimin varallisuus yhtäkkiä kasvaa 1 000 dollarista 1 100 dollariin ja Johnin varallisuus yhtäkkiä kasvaa 10 000 000 dollarista 11 000 000 dollariin, he molemmat kokevat saman onnellisuuden kasvun, koska molemmissa tapauksissa heidän varallisuutensa kasvoi 10 %. Olettaen, että rahan tuoma onnellisuus on todellakin verrannollinen rahan määrän logaritmiin, seuraava taulukko näyttää suurimman summan, jonka jonkun tulisi olla valmis maksamaan varallisuutensa mukaan ennen pelaamisesta maksamista.

Välinpitämättömyys Pelimäärä

Varallisuus Välinpitämättömyys
Määrä
10 dollaria 4,97 dollaria
100 dollaria 7,79 dollaria
1 000 dollaria 10,96 dollaria
10 000 dollaria 14,26 dollaria
100 000 dollaria 17,78 dollaria
1 000 000 dollaria 20,88 dollaria
10 000 000 dollaria 24,19 dollaria
100 000 000 dollaria 27,51 dollaria
1 000 000 000 dollaria 30,84 dollaria


Kuten näet, realistisissa olosuhteissa maksamasi summa on paljon pienempi kuin $∞. Jos esimerkiksi varallisuutesi on miljoona dollaria, sinun pitäisi olla yhdentekevä pelaamisen suhteen, jos hinta on 20,88 dollaria.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Michiganin arpajaisissa on kolmen pelaajan peli, jossa on seuraavat säännöt:

  1. Pelaajat pelaavat yksi kerrallaan, kun taas aloittamattomat pelaajat pidetään poissa lavalta, eikä heille anneta tietoa edellisten pelaajien suorituksista.
  2. Kortteja on 100, numeroitu 1-100.
  3. Pelaaja aloittaa valitsemalla minkä tahansa kortin.
  4. Katsottuaan sitä pelaaja voi pitää sen tai vaihtaa uuteen korttiin.
  5. Kaikki kortit jaetaan uusilla korteilla. Toisin sanoen vanhat kortit laitetaan takaisin pakkaan, myös hylättyinä.
  6. Pelaaja, joka nostaa korkeimman kortin, voittaa.


Onko tässä pelissä viimeisenä pelaamisesta mitään pelipaikkaetua? Mikä on optimaalinen strategia kullekin pelaajalle?

Tässä onYouTube- video, joka näyttää pelin.

Dween

Ensinnäkin viimeisenä toimimisesta ei ole asemaetua. Koska pelaajat pidetään äänieristetyssä kopissa aiempien pelaajien pelatessa, järjestyksellä ei ole väliä.

Toiseksi pelissä on oltava Nash-tasapainotila, jossa strategia, jossa pysytään vähintään x pisteen pistemäärällä, on parempi kuin mikään muu strategia. Kysymys on x:n löytämisestä.

Kysyin itseltäni, mikä olisi strategia, jos jokainen pelaaja saisi 1–100-numeroisen kortin sijaan satunnaisluvun tasaisesti nollan ja yhden välille ja etsin pistettä x, jossa täydellinen loogikko ei välittäisi jäämisensä ja korttinsa vaihtamisen välillä. Tämän vastauksen avulla on helppo soveltaa vastausta diskreettiin jakaumaan välillä 1–100.

Lopetan puhumisen tähän ja annan lukijoideni nauttia ongelmasta. Katso vastaukset ja ratkaisut alla olevista linkeistä.

Vastaus jatkuvalle jakaumalle välillä 0 ja 1 .

Vastaus diskreetille jakaumalle välillä 1-100.

Ratkaisuni löydät napsauttamalla tästä (PDF) .

Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .

Oletetaan, että sinulla on pakka, jossa on kymmenen punaista ja kymmenen mustaa korttia. Satunnaisen sekoittamisen jälkeen nostat kortteja ilman takaisinottoa. Mikä on todennäköisyys, että nostat kaikki kymmenen mustaa korttia ennen kuin nostat viisi punaista korttia?

Don

Se on sama kuin kysyä todennäköisyyttä, että 14 satunnaisen kortin joukossa on kaikki 10 mustaa korttia. Pakassa olevien 10 kortin joukosta on mahdollista valita 4 punaista korttia combin (10,4)=210 tavalla. Kaikki kymmenen mustaa korttia voi tietenkin valita vain yhdellä tavalla. Pakassa olevien 14 kortin joukosta voi valita 10 korttia combin(20,14)=38 760 tavalla. Joten vastaus on 210/38 760=0,005418 eli 1/184,57.

Tiedän kampanjan, jossa bonus maksetaan, kun kaikilla 13 rivillä on neloset. Kuinka monta kättä tämä keskimäärin vaatii?

AxelWolf

Katsotaanpa videopokerin kultastandardia, 9-6 Jacks or Betteria, vastataksemme kysymykseesi.

Ensimmäinen vaihe on muokata laskurini lisäämään rivikohta kaikille 13 nelosille. Tässä on muokattu palautustaulukko:

Muokattu Jacks or Better -palautustaulukko

Tapahtuma Maksaa Yhdistelmät Todennäköisyys Palata
Kuningasvärisuora 800 493 512 264 0,000025 0,019807
Värisuora 50 2 178 883 296 0.000109 0,005465
Neljä A 25 3 900 253 596 0.000196 0,004892
Neljä K:ta 25 3 904 533 816 0.000196 0,004897
Neljä Q:ta 25 3 898 370 196 0.000196 0,004889
Neljä J:tä 25 3 886 872 684 0.000195 0,004875
Neljä 10 25 3 471 687 732 0.000174 0,004354
Neljä 9 25 3 503 226 684 0,000176 0,004394
Neljä 8 25 3 504 128 652 0,000176 0,004395
Neljä 7 25 3 504 825 252 0,000176 0,004396
Neljä 6 25 3 504 861 888 0,000176 0,004396
Neljä 5 25 3 504 895 944 0,000176 0,004396
Neljä 4 25 3 504 032 676 0,000176 0,004395
Neljä 3 25 3 503 177 148 0,000176 0,004394
Neljä 2 25 3 502 301 496 0,000176 0,004393
Täyskäsi 9 229 475 482 596 0.011512 0.103610
Huuhtele 6 219 554 786 160 0.011015 0,066087
Suoraan 4 223 837 565 784 0.011229 0,044917
Kolmoset 3 1 484 003 070 324 0,074449 0,223346
Kaksi paria 2 2 576 946 164 148 0,129279 0,258558
Jacks or Better 1 4 277 372 890 968 0,214585 0,214585
Ei mitään 0 10 872 274 993 896 0,545435 0.000000
Kokonais 19 933 230 517 200 1.000000 0,995439


Todennäköisyys saada neloset samanlaisiksi on 0,002363.

Seuraavaksi on vastattava siihen, kuinka monta nelosta keskimäärin tarvitaan, jotta saadaan kaikki 13 lajia? Vastatakseni tähän kysymykseen loin odotusarvoisten yritysten laskurin . Käyttääksesi sitä, syötä kunkin nelonen yhdistelmien lukumäärä ensimmäisiin 13 soluun. Laskin kertoo, että kaikkien 13 lajin saamiseksi tarvitaan odotettavissa oleva määrä 41,532646 nelosta.

Joten odotettu pelattujen käsien määrä kaikkien 13 nelosten saamiseksi on 41,341739 / 0,002363 = 17 580.

Ruohikko voi ruokkia täsmälleen:

Yksi lehmä ja yksi laama 21 päivän ajan.
Yksi laama ja yksi lammas 42 päivän ajan.
Yksi lammas ja yksi lehmä 28 päivän ajan.
Lehmä syö yhtä paljon ruohoa kuin laama ja lammas yhteensä.
Ruoho kasvaa tasaista vauhtia.

Kuinka kauan kolmella eläimellä kestää yhdessä ahmia kokonaan ruohopelto?

MatiX

[spoileri] Olkoon:
c = lehmän ruohonsyöntinopeus
l = laaman ruohonsyöntinopeus
s = ruohonsyöntinopeus lampailla
g = ruohon kasvunopeus

Tietyn ajanjakson lopussa kulutetun ruohon määrän on oltava yhtä suuri kuin alkuperäinen ruohon määrä plus kyseisenä aikana kasvaneen ruohon määrä. Joten...

(1) 21 * (c + l) = 1 + 21 g
(2) 42 * (l + s) = 1 + 42 g
(3) 28 * (s + c) = 1 + 28 g

Jossa 1 edustaa yhtä nurmikenttää.

Meille annetaan myös:

(4) c=s+l

Ensin sijoitetaan yhtälö (4) yhtälöön (2):

(5) 42c = 1 + 42g

Ilmaise se g:n avulla:

(6) g = (42c⁻¹)/42

Seuraavaksi sijoitetaan yhtälö (6) yhtälöön (1)...

(7) 21(c+l) = 1 + 21*(42c-1)/42

Pienen algebran jälkeen saamme...

(8) l = 1/42.

Seuraavaksi sijoitetaan yhtälö (4) yhtälöön (3)...

(9) 28 * (2s + l) = 1 + 28 g

Tiedämme, että l=1/42, joten...

28 * (2 s + 1/42) = 1 + 28 g
56s + 28/42 = 1 + 28g
2352 s + 28 = 42 + 1176 g
(10) g = (2352s - 14)/1176

Seuraavaksi sijoitetaan yhtälöt (8) ja (10) yhtälöön (2) ...

42*(1/42 + s) = 1 + 42*(2352 s - 14)/1176

Helpon algebran jälkeen saamme:

(11) s = 14/1176 = 1/84

Yhtälöstä (4)

(12) c = (1/84) + (1/42) = 3/84 = 1/28

Jos ruoho ei kasvaisi, lehmällä kestäisi 28 päivää syödä pelto, laamalla 42 ja lampaalla 84.

Ratkaistaan seuraavaksi g. Sijoitetaan (11) yhtälöön (10):

g = [2352*(1/84)-14]/1176
(13) g = 14/1176 = 1/84.

Tämä on sattumalta sama nopeus, jolla lampaat syövät ruohoa.

Olkoon t lopullinen vastaus. Tiedämme, että t päivässä syödyn ruohon määrän on oltava yhtä suuri kuin pellolla olevan ruohon määrä (1) plus sinä aikana kasvanut ruoho. Joten...

(13) t*(s+l+c) = 1 + tg

Ratkaisemassa t...

t*[(1/84) + (1/42) + (1/28)] = 1 + t/84
t = 1/[(1/84) + (1/42) + (1/28) - (1/84)]
(14) t = 84/5 = 16,8 päivää = 16 päivää, 19 tuntia, 12 minuuttia

[/spoiler]

Tämä kysymys nostettiin esiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa.

Mikä on kahden satunnaisen pisteen keskimääräinen etäisyys yksikköneliössä?

anonyymi

Näin helposti esitettävään kysymykseen ratkaisu on melkoisen monimutkainen. Kuten minä tein, sinun on tiedettävä tämä integraali .

Tässä on vastaus ja ratkaisuni (PDF) .

Mikä oli liitutaululla oleva matemaattinen tehtävä elokuvassa Hyvä Will Hunting ?

anonyymi

Se oli itse asiassa melko helppoa, varsinkin MIT:n kombinatorisen matematiikan kurssilla. Tässä on tehtävän sanamuoto:

"Piirrä kaikki homeomorfisesti redusoitumattomat puut, joiden koko on n=10."

Tässä on yritykseni ilmaista se selkeällä ja yksinkertaisella englannilla.

Piirrä suoria viivoja käyttäen kaikki kuviot, joissa leikkauspisteiden ja umpikujien summa on 10. Suljettuja silmukoita ei saa olla. Myöskään kahta samanarvoista kuviota ei saa olla. Mistä tahansa risteyksestä on johdettava vähintään kolme polkua.

Saatat kysyä, mitä tarkoitan "ekvivalenssilla"? Se tarkoittaa, että voit siirtää paloja haluamallasi tavalla jättäen leikkauspisteet rauhaan, eikä se luo uusia kuvioita.

Tässä on esimerkki: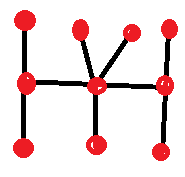



Annanpa vinkin. Toisin kuin elokuvan vastauksessa, niitä on kymmenen. Willillä on niitä vain kahdeksan. Katso, pystytkö samaan tai voittamaan Will Huntingin.

[spoileri]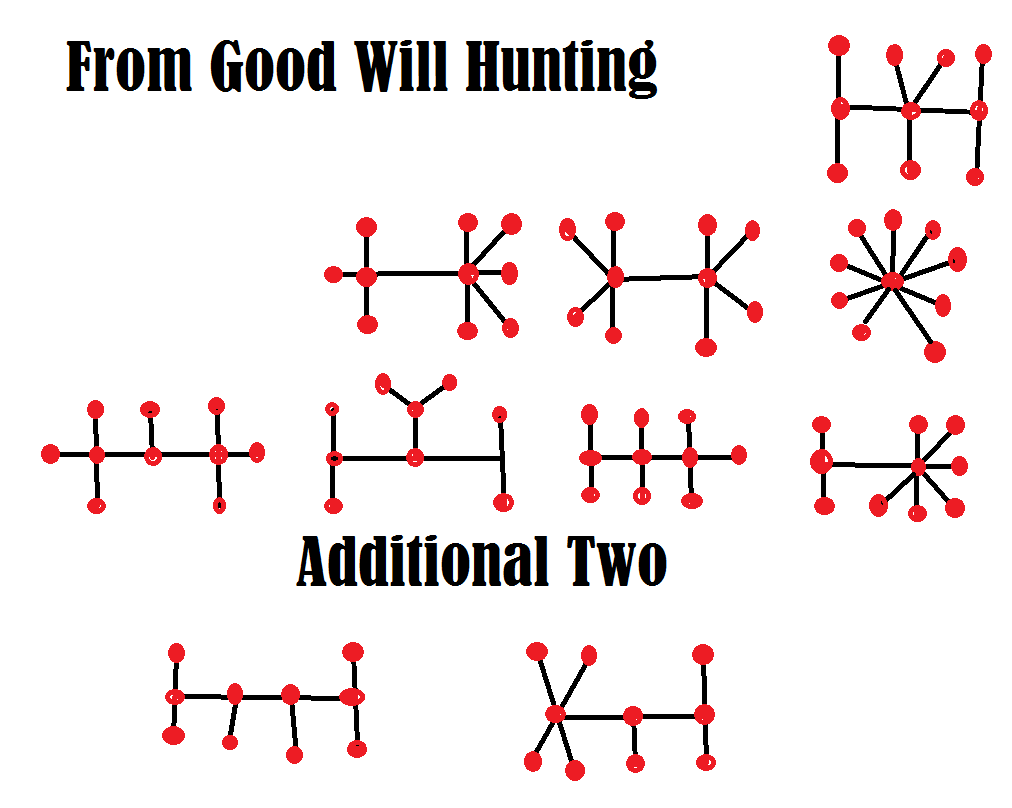

Näytän logiikkani kaikkien kymmenen keksimiselle MathProblems.info -sivustollani, tehtävässä 220.

[/spoiler] Lisälukemista:



Harkitse peliä, jossa on seuraavat säännöt:

  • Satunnaislukugeneraattori tuottaa tasaisesti jakautuneita satunnaislukuja väliltä 0 ja 1.
  • Kaksi pelaajaa saa kumpikin oman numeronsa. Jokainen pelaaja näkee vain oman numeronsa.
  • Pelaaja 1 voi pitää alkuperäisen numeronsa tai vaihtaa sen uuteen satunnaiseen lukuun.
  • Pelaajalla 2, joka tietää pelaajan 1 toiminnan, on sama vaihtoehto: pitää alkuperäinen numeronsa tai vaihtaa se uuteen.
  • Suuremman numeron saanut pelaaja voittaa.

Minulla on neljä kysymystä pelistä:

  1. Vastaa seuraaviin pelistä kertoviin kysymyksiin:
  2. Millä numerolla pelaaja 1 ei voi päättää, nouseeko hän seisomaan vai vaihtaako hän pöytää?
  3. Olettaen, että pelaaja 1 vaihtaa korttia, millä numerolla pelaajan 2 pitäisi olla välinpitämätön siitä, jääkö hän seisomaan vai vaihtaako hän korttia?
  4. Olettaen, että pelaaja 1 jää seisomaan, millä numerolla pelaajan 2 pitäisi olla yhdentekevä siitä, jääkö hän seisomaan vai vaihtaako hän paikkaa?
  5. Olettaen, että molemmat pelaajat toimivat optimaalisella strategialla, mikä on todennäköisyys, että pelaaja 1 voittaa?

anonyymi

Vastaus ja ratkaisu löytyvät Matematiikkatehtävät- sivultani, tehtävä 225.

Osallistun vuoden 2018 "kuolleen altaan" turnaukseen. Tässä ovat säännöt:

  1. Jokaisen pelaajan on lähetettävä lista kymmenestä elossa olevasta alle 100-vuotiaasta julkkiksesta.
  2. Jos jokin julkkis kuolee, kuten Associated Pressin maininta osoittaa vuonna 2018, kuka tahansa, jonka nimi on julkkiksen listalla, saa 100-x pistettä, jossa x on kuolinikä.
  3. Eniten pisteitä 1.1.2019 kerännyt pelaaja voittaa.

Keskiarvoista poiketen, mikä on optimaalinen strategia tälle pelille?

anonyymi

Entisenä aktuaarina kysyit oikealta henkilöltä. Toivottavasti aktuaariyhdistys ei pidä vastaustani ammatin väärinkäytönä. Vastatakseni kysymykseesi tutustuin kuitenkin vuoden 2014 elinaikataulukkoon entisestä työpaikastani, Sosiaaliturvaviranomaisen pääaktuaarin toimistosta.

Elinkaaren taulukko näyttää muun muassa minkä tahansa ikäisen ja sukupuolen henkilön kuoleman todennäköisyyden vuonna 2014. Näiden tietojen avulla loin seuraavan taulukon, joka näyttää sekä kuoleman todennäköisyyden että odotetut pisteet kaikille ikäryhmille 0–100 ja molemmille sukupuolille.

Vuoden 2014 elinikäisten ja kuolleiden taulukko

Ikä Todennäköisyys
Kuolema — Mies		 Todennäköisyys
Kuolema — Nainen		 Odotettu
Pisteet — Mies		 Odotettu
Pisteet — Naiset
0 0,006320 0,005310 0,632000 0,531000
1 0,000403 0,000352 0,039852 0,034835
2 0,000282 0,000221 0,027626 0,021683
3 0.000211 0.000161 0,020514 0,015612
4 0.000181 0,000131 0,017405 0,012556
5 0.000161 0.000111 0,015313 0,010515
6 0,000141 0.000111 0,013260 0,010405
7 0,000131 0.000101 0,012184 0,009360
8 0.000121 0,000091 0.011127 0,008334
9 0,000091 0.000081 0,008256 0,007328
10 0.000101 0,000091 0,009073 0,008154
11 0.000101 0.000081 0,008973 0,007168
12 0,000131 0.000101 0,011535 0,008861
13 0,000202 0,000131 0,017547 0.011389
14 0,000303 0,000151 0,026023 0,012992
15 0.000404 0.000191 0,034304 0,016267
16 0.000505 0,000232 0,042393 0,019464
17 0,000616 0,000272 0,051129 0,022582
18 0,000748 0,000302 0,061316 0,024796
19 0.000880 0,000343 0,071262 0,027768
20 0,001022 0,000373 0,081780 0,029855
21 0.001145 0.000404 0,090445 0,031884
22 0.001258 0.000444 0,098105 0,034643
23 0.001310 0,000475 0.100880 0,036546
24 0,001332 0,000495 0.101246 0,037625
25 0,001344 0,000526 0.100811 0,039422
26 0,001377 0,000556 0.101864 0,041162
27 0,001389 0,000577 0.101371 0,042106
28 0,001421 0,000608 0.102330 0,043740
29 0.001454 0,000648 0.103234 0,046036
30 0,001507 0,000669 0.105517 0,046837
31 0.001530 0.000710 0.105584 0,048998
32 0,001574 0,000751 0.107011 0,051084
33 0,001617 0,000813 0.108364 0,054454
34 0,001661 0.000864 0.109644 0,057041
35 0.001716 0,000926 0.111521 0,060194
36 0,001781 0.001008 0.113970 0,064538
37 0,001857 0,001081 0.116963 0,068090
38 0,001933 0.001164 0.119830 0,072145
39 0.002020 0,001237 0.123207 0,075427
40 0.002118 0.001340 0.127066 0,080422
41 0,002258 0.001445 0,133232 0,085232
42 0.002410 0,001560 0,139778 0,090455
43 0,002615 0,001696 0,149075 0,096649
44 0,002843 0,001853 0,159228 0.103761
45 0,003105 0.002011 0,170771 0.110606
46 0,003401 0,002191 0,183635 0.118300
47 0,003742 0,002403 0.198314 0,127342
48 0,004108 0,002647 0,213613 0,137656
49 0,004532 0,002894 0.231133 0,147577
50 0,004994 0,003194 0,249696 0.159718
51 0,005473 0,003487 0,268191 0.170880
52 0,005993 0,003794 0,287656 0.182103
53 0,006565 0,004104 0.308561 0.192871
54 0,007159 0,004428 0,329324 0,203676
55 0,007799 0,004767 0,350946 0,214498
56 0,008475 0,005153 0,372902 0,226729
57 0,009179 0,005534 0,394696 0,237972
58 0,009856 0,005889 0,413944 0,247347
59 0,010575 0,006272 0,433558 0,257150
60 0.011350 0,006683 0,453991 0,267338
61 0.012209 0,007180 0,476135 0.280016
62 0,013061 0,007720 0.496330 0,293355
63 0,013921 0,008339 0,515084 0.308537
64 0,014814 0,009029 0,533320 0,325041
65 0,015831 0,009839 0,554094 0,344371
66 0,016981 0,010741 0,577354 0,365197
67 0,018300 0,011752 0.603909 0.387812
68 0,019778 0,012879 0,632894 0.412117
69 0,021443 0,014142 0,664734 0,438397
70 0,023384 0,015613 0.701513 0,468376
71 0,025547 0,017271 0,740873 0.500852
72 0,027877 0,019047 0,780560 0,533320
73 0,030384 0,020918 0.820374 0,564797
74 0,033098 0,022938 0,860535 0,596385
75 0,036256 0,025299 0,906400 0,632465
76 0,039868 0,028043 0,956841 0,673035
77 0,043883 0,031127 1.009299 0,715914
78 0,048257 0,034590 1.061657 0,760984
79 0,053128 0,038456 1.115692 0.807583
80 0,058709 0,043007 1.174177 0.860145
81 0,065070 0,048186 1.236322 0,915536
82 0,072149 0,053762 1.298691 0,967712
83 0,079906 0,059769 1.358409 1.016065
84 0.088524 0,066380 1.416378 1.062085
85 0,098157 0.073823 1.472348 1.107351
86 0.108904 0,082381 1.524651 1.153334
87 0.120889 0,092180 1.571556 1.198344
88 0.134134 0.103305 1.609607 1.239664
89 0.148707 0.115744 1.635778 1.273180
90 0,164522 0,129477 1.645220 1.294772
91 0.181584 0.144435 1.634254 1.299911
92 0.199903 0,160621 1.599225 1.284970
93 0,219362 0.177816 1.535534 1.244713
94 0,239881 0.196194 1.439286 1.177165
95 0,260293 0,214694 1.301463 1.073469
96 0.280129 0,233056 1.120515 0,932225
97 0,299042 0,251152 0.897125 0,753456
98 0,316317 0,268235 0,632634 0,536471
99 0,332667 0,284442 0,332667 0,284442
100 0.348651 0.301417 0.000000 0.000000

Taulukosta käy ilmi, että 90-vuotiaan miehen odotettu enimmäispistemäärä on 1,645220.

Tätä kysymystä on käsitelty ja siitä keskustellaan uhkapeleihin liittymättömällä Diversity Tomorrow -foorumillani.

Jos haluat sulkea 355 millilitraa tölkkiin, mitkä tulisi olla mittojen olla pinta-alan minimoimiseksi?

anonyymi

Hyvä kysymys! Mietin juuri tätä, kun näin pelimessuilla ohuita limsatölkkejä, joissa oli tavalliset 355 millilitraa tilavuutta. Kumpikaan ei varmasti voi pitää paikkaansa (älkääkä kutsuko minua Shirleyksi). [juonnejuonne] Olkoonpa:
r = tölkin säde
h = tölkin korkeus
v = tölkin tilavuus
s = tölkin pinta-ala

Yksinkertaisesta geometriasta tiedämme, että pinta-ala = 2*pii*r^2 + 2*pii*r*h.

Samoin tiedämme myös, että tilavuus on pi*r^2*h, jonka meille annetaan olevan yhtä kuin 355.

Joten 355 = pi*r^2*h.

Järjestetäänpä se uudelleen muotoon:

(1) h = 355/(pii*r^2)

Tiedämme:

(2) s = 2*pii*r^2 + 2*pii*r*h.

Muutetaan se yhden muuttujan funktioksi sijoittamalla yhtälön (1) h-lausekkeemme yhtälöön (2):

s = 2*pi*r^2 + + 2*pi*r*(355/(pi*r^2))) = 2*pi*r^2 + 710/r.

Otetaan s:n derivaatta ja asetetaan se nollaksi optimaalisen r:n ratkaisemiseksi.

ds/dr = 4*pi*r - 710/(r^2) = 0

4*pii*r = 710/(r^2)

Kertomalla molemmat puolet r^2:lla:

4*pii*r^3 = 710

r^3 = 177,5/pi.

r = (177,5/pi)^(1/3) = 3,837215248.

Syötä tämä arvo yhtälöön (1) saadaksesi h = 7.674430496.[/spoiler]

kaksi tölkkiä -- käännettyinä

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Minusta tuntuu, että useimmat tuntemani uhkapelialan ammattilaiset haluavat tietää pelin volatiliteetin varianssina ilmaistuna mieluummin kuin keskihajontana. Ensimmäinen on tietenkin vain jälkimmäisen neliö. Itse pidän kuitenkin keskihajonnasta enemmän, koska se ilmaistaan samoissa yksiköissä kuin panos ja voitto/häviö. Ehkä he pitävät suuremmasta luvusta, jotta suurempi volatiliteetti erottuu? Mikä on sinun näkemyksesi – käyttävätkö pelaajat mieluummin "varianssia" ja jos käyttävät, niin miksi?

Gary J. Koehler

Olen samaa mieltä siitä, että pelin varianssista puhutaan useammin kuin sen keskihajonnasta, mikä on aina ollut hieman ärsyttävää. Mielestäni uhkapelureiden tulisi välittää pelin volatiliteetista siksi, että he voivat yhdistää voiton tai tappion todennäköisyyteen pelisession aikana. Esimerkiksi mikä olisi 1 %:n huono tappio 200 blackjack-käden jälkeen? Vastauksena tähän käyttäisit blackjackin keskihajontaa, joka on noin 1,15 säännöistä riippuen.

Tarkka vastaus tähän kysymykseen on 1,15 × 200^0,5 × -2,32635 (joka on Gaussin käyrän 1 prosenttipiste) = -37,83 yksikköä odotuksesta etelään. Älä unohda, että talon edun vuoksi voit odottaa häviäväsi jotakin. Jos oletamme talon edun olevan 0,3 %, niin 200 käden jälkeen voit odottaa häviäväsi 0,003 * 200 = 0,6 kättä. Joten 1 %:n huono tappio olisi 0,6 + 37,83 = 38,43 kättä.

Olen kuullut, että avioliiton päättymisen todennäköisyys, jonka Yhdysvalloissa yleensä sanotaan olevan 50 %, lasketaan suhteuttamalla avioerojen lukumäärä saman ajanjakson aikana solmittujen avioliittojen lukumäärään. Onko se totta? Pidätkö sitä oikeudenmukaisena tapana laskea tilastoa? Kyseenalaistan sen, koska vertaat avioeroja lyhyen ajan kuluessa solmittuihin avioliittoihin pitkän ajan kuluessa.

Gialmere

Jos väestö ja ikäjakauma pysyisivät vakaina ja avioeron todennäköisyys olisi todella 50 %, odottaisimme suuren otoskoon perusteella näkevämme yhden avioeron ja kahden avioliiton suhteen millä tahansa ajanjaksolla.

Väestö ei kuitenkaan ole vakaa. Tästä kaaviosta näyttää siltä, että Yhdysvaltojen väestö kasvaa 10,71 % vuosikymmenessä. Se tekee 1,02 % vuodessa. Sanotaanpa vain 1 % yksinkertaisuuden vuoksi.

Yhdysvaltain väestö

Karttalähde: Yhdysvaltain väestönlaskenta

Fatherly.comin mukaan epäonnistuneen avioliiton keskimääräinen pituus on 8 vuotta.

Jos tarkkailisit avioerojen ja avioliittojen suhdetta nykyhetkellä 1:2, mikä olisi keskimääräinen todennäköisyys sille, että jokin tietty avioliitto päättyy avioeroon?

Nykyiset avioerot solmittiin kahdeksan vuotta sitten, jolloin väestö oli 92,35 % nykyisestä. Yksinkertainen matematiikka viittaa siihen, että avioeron todellinen todennäköisyys on 54,14 %.

Tarkistetaanpa se.

Ensinnäkin CDC:n mukaan vuosittain solmitaan 6,9 avioliittoa 1 000 asukasta kohden. Tämä luku ei ole relevantti käsillä olevan kysymyksen kannalta, mutta mielestäni se auttaa ymmärtämään asiaan liittyviä lukuja.

Oletetaan, että väkiluku oli 8 vuotta sitten 300 000 000. Se olisi 0,69 % * 300 miljoonaa = 2 070 000 avioliittoa sinä vuonna.

Jos 54,14 % heistä päättyy avioeroon kahdeksan vuotta myöhemmin, niin näkisimme 2 070 000 * 54,14 % = 1 120 698 avioeroa nykyhetkellä.

1 120 698 / 2 070 000 = 50 % havaittu avioerojen ja avioliittojen suhde nykyhetkellä.

Jotta kukaan ei sitä sanoisi, tiedän kyllä, etteivät kaikki avioerot pääty tasan kahdeksaan vuoteen. Kaiken kaikkiaan kuitenkin sanon, että lopputulos ei ole kaukana todellisesta 54,14 prosentin avioeroprosentistani.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Toimistossasi sadan työntekijän ryhmässä järjestetään salainen joulupukin lahjavaihto. Siinä kirjoitetaan kaikkien nimet yksittäisille paperilapuille, laitetaan ne hattuun ja jokainen arpoo satunnaisesti nimen, jolle hän antaa lahjan.

Kysymys kuuluu, kuinka monta suljettua silmukkaa keskimäärin on? Esimerkiksi suljetussa silmukassa Gordon antaa Donille, joka antaa Jonille, joka antaa Nathanille ja joka antaa Gordonille. Tai oman nimesi arpominen.

anonyymi

Harkitse, että jokainen valitsee yhden kerrallaan. Kun jokainen valitsee, on kahdenlaisia tilanteita:

  1. Valittavan nimi on jo valittu.
  2. Valitun nimi on edelleen nimilaatikossa.

Oletetaan, että mille tahansa poimijalle on jäljellä n henkilöä poimittavana.

Jos valitsevan henkilön nimi on jo valittu, on 1/n todennäköisyys, että valitseja valitsee oman nimensä sisältävän silmukan. Oletetaan esimerkiksi, että Amy valitsee. Amyn nimi on jo Bobin hallussa, Bobin nimi on jo Charlien hallussa ja Charlien nimi on edelleen laatikossa. Kun laatikossa on vielä n nimeä, on 1/n todennäköisyys, että Amy valitsee Charlien nimen, mikä sulkee silmukan.

Jos valitsevan henkilön nimeä ei ole vielä valittu, on 1/n mahdollisuus, että Amy valitsee oman nimensä, jolloin silmukka sulkeutuu.

Joka tapauksessa, jos poimija ei sulje silmukkaa, hän liittyy osaan toista ketjua, jonka joku muu lopulta sulkee. Jokainen ketju lasketaan vain kerran, kun se sulkeutuu.

Näin ollen vastaus on 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5,187377518.

Riittävän suurelle pelaajien määrälle n saadaan arvio ln(n).

Kysymys on esitetty ja siitä keskustellaan foorumillani Wizard of Vegasissa .

Kysy velholta -palstan #314 kunniaksi, mitkä ovat suosikkisi äärettömistä sarjoista, jotka summautuvat johonkin piin funktioon?

Heather

Nämä kaksi on helppo valita, luultavasti kahdeksi tunnetuimmaksi:

  • 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4
  • 1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + ... = π^2/6

Olen kuullut, että 23 satunnaisen ihmisen ryhmässä on yli 50 % todennäköisyys sille, että kahdella tai useammalla ihmisellä on yhteinen syntymäpäivä? Pitääkö tämä paikkansa? Mikä on todennäköisyys sille, että muilla ryhmillä on yhteinen syntymäpäivä? Sama kysymys koskee myös 3, 4 ja 5 ihmisen yhteistä syntymäpäivää.

anonyymi

Tämä on totta, että 23 satunnaisen ihmisen tapauksessa todennäköisyys sille, että ainakin yhdellä ihmisparilla on yhteinen syntymäpäivä, on 50,73 %. Tämä jättää huomiotta karkauspäivän ja olettaa, että kaikilla on yhtäläinen mahdollisuus syntyä jokaisena muuna 365 päivänä (mikä ei todellisuudessa pidä paikkaansa, sillä kevään ja syksyn syntymäpäivät ovat hieman yleisempiä).

Kysymykseesi vastanneet taulukot ovat lainausmerkkien pituisia, joten laitan ne spoileritunnisteiden sisään. Klikkaa painikkeita nähdäksesi vastaukset.

Yhteinen syntymäpäivä kahdelle+ hengelle

Ryhmän koko Todennäköisyys
2 0,002740
3 0,008204
4 0,016356
5 0,027136
6 0,040462
7 0,056236
8 0,074335
9 0,094624
10 0.116948
11 0.141141
12 0,167025
13 0.194410
14 0.223103
15 0,252901
16 0.283604
17 0.315008
18 0.346911
19 0.379119
20 0.411438
21 0,443688
22 0,475695
23 0,507297
24 0,538344
25 0,568700
26 0.598241
27 0,626859
28 0,654461
29 0.680969
30 0,706316
31 0,730455
32 0,753348
33 0,774972
34 0,795317
35 0,814383
36 0,832182
37 0.848734
38 0,864068
39 0.878220
40 0.891232
41 0,903152
42 0.914030
43 0,923923
44 0,932885
45 0,940976
46 0,948253
47 0,954774
48 0,960598
49 0,965780
50 0,970374
51 0,974432
52 0,978005
53 0.981138
54 0,983877
55 0,986262
56 0,988332
57 0,990122
58 0,991665
59 0,992989
60 0,994123
61 0,995089
62 0.995910
63 0.996604
64 0,997190
65 0,997683
66 0.998096
67 0.998440
68 0,998726
69 0.998964
70 0.999160
71 0,999321
72 0,999453
73 0,999561
74 0,999649
75 0.999720
76 0,999777
77 0.999824
78 0,999861
79 0,999891
80 0.999914
81 0,999933
82 0,999948
83 0.999960
84 0,999969

Yhteinen syntymäpäivä 3+ hengelle

Ryhmän koko Todennäköisyys
3 0.000008
4 0.000030
5 0,000075
6 0.000149
7 0,000261
8 0,000416
9 0,000623
10 0.000888
11 0.001218
12 0,001621
13 0,002102
14 0,002670
15 0,003329
16 0,004088
17 0,004953
18 0,005929
19 0,007024
20 0,008243
21 0,009592
22 0.011078
23 0,012705
24 0,014481
25 0,016409
26 0,018497
27 0,020747
28 0,023167
29 0,025760
30 0,028531
31 0,031484
32 0,034624
33 0,037954
34 0,041479
35 0,045202
36 0,049126
37 0,053254
38 0,057589
39 0,062133
40 0,066889
41 0,071859
42 0,077044
43 0,082446
44 0,088065
45 0,093903
46 0,099960
47 0.106236
48 0.112731
49 0.119444
50 0,126375
51 0,133522
52 0.140885
53 0.148460
54 0,156246
55 0,164241
56 0,172441
57 0.180844
58 0.189445
59 0.198242
60 0.207230
61 0,216405
62 0,225761
63 0,235294
64 0,244999
65 0,254869
66 0,264899
67 0,275082
68 0,285413
69 0,295883
70 0,306487
71 0,317217
72 0.328066
73 0,339026
74 0.350088
75 0.361246
76 0,372491
77 0.383814
78 0,395207
79 0,406662
80 0,418169
81 0,429720
82 0,441307
83 0,452920
84 0,464550
85 0,476188
86 0.487826
87 0.499455
88 0,511065
89 0,522648
90 0,534196
91 0,545698
92 0,557148
93 0,568537
94 0,579855
95 0,591096
96 0.602252
97 0,613314
98 0,624275
99 0,635127
100 0,645865
101 0,656480
102 0,666967
103 0,677318
104 0.687529
105 0,697593
106 0.707505
107 0,717260
108 0,726853
109 0,736279
110 0,745536
111 0,754619
112 0,763525
113 0,772251
114 0,780795
115 0,789155
116 0,797330
117 0.805319
118 0.813121
119 0.820580
120 0,827964
121 0,835152
122 0.842144
123 0.848940
124 0,855540
125 0,861945
126 0.868155
127 0,874172
128 0,879996
129 0.885631
130 0,891076
131 0,896335
132 0.901409
133 0,906302
134 0.911015
135 0,915552
136 0,919915
137 0,924108
138 0,928135
139 0,931997
140 0,935700
141 0,939246
142 0,942640
143 0,945885
144 0,948985
145 0,951944
146 0,954766
147 0,957456
148 0,960016
149 0,962452
150 0,964767
151 0,966965
152 0,969050
153 0,971028
154 0,972900
155 0,974672
156 0,976347
157 0,977930
158 0,979423
159 0.980831
160 0.982158
161 0,983407
162 0,984581
163 0,985684
164 0.986719
165 0,987690
166 0.988600
167 0,989452
168 0,990248
169 0,990992
170 0,991687
171 0,992335
172 0,992938
173 0,993500
174 0,994022
175 0,994508
176 0,994958
177 0,995376
178 0,995763
179 0,996121
180 0,996452
181 0,996758
182 0.997040
183 0,997300
184 0.997540
185 0,997760
186 0,997963
187 0.998149
188 0.998319
189 0,998476
190 0.998619
191 0,998750
192 0.998869
193 0,998979
194 0,999078
195 0,999169
196 0,999251
197 0,999326
198 0,999394
199 0.999456
200 0,999512
201 0,999562
202 0,999608
203 0,999650
204 0,999687
205 0.999720
206 0,999751
207 0,999778
208 0,999802
209 0.999824
210 0.999844
211 0,999862
212 0,999877
213 0,999891
214 0.999904
215 0.999915
216 0,999925
217 0.999934
218 0,999942
219 0,999949
220 0,999955
221 0,999961
222 0,999966
223 0.999970
224 0,999974
225 0,999977
226 0.999980
227 0,999982
228 0,999985
229 0,999987
230 0,999988
231 0.999990
232 0,999991
233 0,999992
234 0,999994
235 0,999994
236 0,999995
237 0,999996
238 0,999996
239 0,999997
240 0,999997
241 0,999998
242 0,999998
243 0,999998
244 0,999999

Yhteinen syntymäpäivä 4+ hengelle

Ryhmän koko Todennäköisyys
4 0.000000
5 0.000000
6 0.000000
7 0.000001
8 0.000001
9 0,000003
10 0.000004
11 0.000007
12 0.000010
13 0.000014
14 0.000020
15 0,000027
16 0.000036
17 0.000048
18 0,000061
19 0,000077
20 0.000096
21 0.000119
22 0.000145
23 0,000175
24 0.000209
25 0,000248
26 0,000293
27 0,000343
28 0,000399
29 0,000462
30 0,000532
31 0.000610
32 0,000695
33 0,000790
34 0,000893
35 0,001006
36 0.001129
37 0,001263
38 0.001408
39 0,001566
40 0,001736
41 0.001919
42 0.002116
43 0,002328
44 0,002555
45 0,002798
46 0,003058
47 0,003334
48 0,003629
49 0,003943
50 0,004276
51 0,004629
52 0,005003
53 0,005399
54 0,005817
55 0,006258
56 0,006724
57 0,007214
58 0,007730
59 0,008272
60 0,008841
61 0,009439
62 0,010065
63 0,010721
64 0.011408
65 0.012126
66 0,012876
67 0,013659
68 0,014476
69 0,015327
70 0,016215
71 0,017139
72 0,018100
73 0,019099
74 0,020137
75 0,021215
76 0,022334
77 0,023495
78 0,024698
79 0,025944
80 0,027235
81 0,028570
82 0,029951
83 0,031379
84 0,032855
85 0,034379
86 0,035952
87 0,037575
88 0,039249
89 0,040974
90 0,042752
91 0,044583
92 0,046467
93 0,048407
94 0,050402
95 0,052453
96 0,054561
97 0,056726
98 0,058950
99 0,061233
100 0,063576
101 0,065978
102 0,068442
103 0,070967
104 0,073554
105 0.076204
106 0,078917
107 0,081694
108 0,084535
109 0,087441
110 0,090412
111 0,093449
112 0,096552
113 0,099722
114 0.102958
115 0,106262
116 0.109633
117 0.113072
118 0.116579
119 0.120154
120 0.123798
121 0.127510
122 0,131292
123 0,135142
124 0,139061
125 0.143050
126 0,147107
127 0.151234
128 0,155429
129 0,159694
130 0,164027
131 0,168429
132 0,172899
133 0,177438
134 0.182044
135 0.186719
136 0.191460
137 0,196269
138 0.201144
139 0,206085
140 0.211091
141 0,216163
142 0,221299
143 0,226499
144 0,231763
145 0,237089
146 0,242476
147 0,247925
148 0,253434
149 0,259002
150 0,264629
151 0,270314
152 0,276055
153 0,281852
154 0.287703
155 0,293608
156 0,299566
157 0,305575
158 0.311634
159 0,317741
160 0,323897
161 0,330099
162 0,336346
163 0,342637
164 0.348970
165 0,355343
166 0,361757
167 0.368208
168 0,374696
169 0.381218
170 0.387774
171 0,394362
172 0.400980
173 0.407626
174 0,414299
175 0,420997
176 0,427718
177 0,434462
178 0.441224
179 0.448005
180 0.454803
181 0,461615
182 0,468439
183 0,475274
184 0.482118
185 0.488969
186 0,495826
187 0,502685
188 0.509546
189 0,516407
190 0,523265
191 0.530119
192 0,536967
193 0,543807
194 0,550636
195 0,557454
196 0,564258
197 0,571046
198 0,577817
199 0,584568
200 0,591298
201 0.598005
202 0.604687
203 0,611342
204 0,617969
205 0,624565
206 0.631129
207 0,637659
208 0.644154
209 0,650611
210 0.657030
211 0,663407
212 0,669743
213 0,676035
214 0,682281
215 0.688481
216 0.694632
217 0.700734
218 0.706784
219 0,712782
220 0,718726
221 0,724614
222 0,730446
223 0,736220
224 0,741936
225 0,747591
226 0,753185
227 0,758717
228 0,764185
229 0,769590
230 0,774929
231 0,780202
232 0,785409
233 0,790547
234 0,795618
235 0.800619
236 0.805551
237 0,810412
238 0,815202
239 0,819921
240 0,824569
241 0.829144
242 0,833646
243 0,838076
244 0,842432
245 0,846716
246 0,850925
247 0,855061
248 0,859123
249 0.863112
250 0,867027
251 0.870868
252 0,874635
253 0,878329
254 0,881950
255 0.885498
256 0.888973
257 0,892375
258 0.895705
259 0.898964
260 0.902151
261 0,905268
262 0.908314
263 0.911290
264 0,914197
265 0,917036
266 0,919806
267 0,922509
268 0,925145
269 0,927715
270 0,930220
271 0,932661
272 0,935037
273 0,937351
274 0,939603
275 0,941793
276 0,943923
277 0,945993
278 0,948005
279 0,949960
280 0,951857
281 0,953699
282 0,955486
283 0,957218
284 0,958898
285 0,960527
286 0,962104
287 0,963631
288 0,965109
289 0,966540
290 0,967923
291 0,969260
292 0,970553
293 0,971802
294 0,973007
295 0,974171
296 0,975294
297 0,976377
298 0,977421
299 0,978427
300 0,979397
301 0.980330
302 0.981228
303 0,982092
304 0,982923
305 0,983722
306 0,984490
307 0,985227
308 0,985935
309 0.986614
310 0,987266
311 0,987890
312 0.988489
313 0.989063
314 0.989612
315 0,990138
316 0,990641
317 0.991122
318 0,991581
319 0.992021
320 0.992440
321 0,992841
322 0,993223
323 0,993587
324 0,993935
325 0,994266
326 0,994581
327 0.994882
328 0,995167
329 0,995439
330 0,995698
331 0,995943
332 0,996176
333 0,996398
334 0,996608
335 0,996807
336 0,996996
337 0,997175
338 0,997344
339 0,997505
340 0,997657
341 0.997801
342 0,997936
343 0,998065
344 0.998186
345 0.998300
346 0.998408
347 0.998510
348 0.998606
349 0,998696
350 0.998781
351 0.998861
352 0,998937
353 0.999008
354 0,999074
355 0,999137
356 0,999195
357 0,999250
358 0,999302
359 0,999350
360 0,999396
361 0,999438
362 0,999478
363 0,999515
364 0,999550
365 0,999582
366 0,999613
367 0,999641
368 0,999668
369 0,999692
370 0,999715
371 0,999736
372 0.999756
373 0,999775
374 0,999792
375 0.999808
376 0.999823
377 0,999837
378 0.999850
379 0,999861
380 0,999872
381 0,999883
382 0,999892
383 0,999901
384 0.999909
385 0.999916
386 0,999923
387 0.999930
388 0,999935
389 0.999941
390 0.999946
391 0.999950
392 0,999955
393 0,999959
394 0,999962
395 0,999965
396 0,999969
397 0,999971
398 0,999974
399 0,999976
400 0,999978
401 0.999980
402 0,999982
403 0.999984
404 0,999985
405 0,999987
406 0,999988
407 0,999989
408 0.999990
409 0,999991
410 0,999992
411 0,999993
412 0,999993
413 0,999994
414 0,999995
415 0,999995
416 0,999996
417 0,999996
418 0,999996
419 0,999997
420 0,999997
421 0,999997
422 0,999998
423 0,999998
424 0,999998
425 0,999998
426 0,999998
427 0,999999
428 0,999999
429 0,999999

Yhteinen syntymäpäivä 5+ hengelle

Ryhmän koko Todennäköisyys
5 0.000000
6 0.000000
7 0.000000
8 0.000000
9 0.000000
10 0.000000
11 0.000000
12 0.000000
13 0.000000
14 0.000000
15 0.000000
16 0.000000
17 0.000000
18 0.000001
19 0.000001
20 0.000001
21 0.000001
22 0,000002
23 0,000002
24 0,000003
25 0.000004
26 0.000004
27 0.000005
28 0.000006
29 0.000008
30 0.000009
31 0.000011
32 0.000013
33 0.000015
34 0.000017
35 0.000020
36 0,000023
37 0.000026
38 0.000030
39 0.000034
40 0.000039
41 0.000044
42 0.000050
43 0.000056
44 0.000063
45 0.000070
46 0.000079
47 0.000087
48 0,000097
49 0.000108
50 0.000119
51 0,000132
52 0.000145
53 0.000159
54 0,000175
55 0,000192
56 0.000209
57 0,000229
58 0,000249
59 0,000271
60 0,000295
61 0,000320
62 0,000347
63 0,000375
64 0,000406
65 0,000438
66 0,000472
67 0,000509
68 0,000547
69 0,000588
70 0,000631
71 0,000676
72 0,000725
73 0,000775
74 0,000829
75 0.000885
76 0.000944
77 0,001007
78 0,001072
79 0.001141
80 0.001213
81 0,001289
82 0,001369
83 0,001452
84 0,001539
85 0,001630
86 0,001726
87 0,001825
88 0.001930
89 0,002038
90 0,002152
91 0,002270
92 0,002394
93 0,002522
94 0,002656
95 0,002796
96 0,002941
97 0,003092
98 0,003249
99 0,003412
100 0,003581
101 0,003757
102 0,003939
103 0,004128
104 0,004325
105 0,004528
106 0.004739
107 0,004957
108 0,005183
109 0,005417
110 0,005659
111 0,005909
112 0,006168
113 0,006436
114 0,006712
115 0,006998
116 0,007293
117 0,007597
118 0,007912
119 0,008236
120 0,008570
121 0,008915
122 0,009270
123 0,009636
124 0,010013
125 0,010402
126 0,010801
127 0.011213
128 0,011637
129 0,012072
130 0,012521
131 0,012981
132 0,013455
133 0,013942
134 0,014442
135 0,014956
136 0,015484
137 0,016026
138 0,016582
139 0,017153
140 0,017739
141 0,018340
142 0,018956
143 0,019588
144 0,020235
145 0,020899
146 0,021580
147 0,022277
148 0,022991
149 0,023722
150 0,024470
151 0,025237
152 0,026021
153 0,026824
154 0,027645
155 0,028485
156 0,029344
157 0,030222
158 0.031120
159 0,032037
160 0,032975
161 0,033934
162 0,034913
163 0,035912
164 0,036934
165 0,037976
166 0,039040
167 0,040127
168 0,041235
169 0,042367
170 0,043521
171 0,044698
172 0,045898
173 0,047122
174 0,048370
175 0,049642
176 0,050939
177 0,052260
178 0,053606
179 0,054977
180 0,056374
181 0,057796
182 0,059245
183 0,060719
184 0,062220
185 0,063748
186 0,065302
187 0,066884
188 0,068493
189 0,070130
190 0,071795
191 0,073487
192 0,075209
193 0,076958
194 0,078737
195 0,080544
196 0,082381
197 0,084247
198 0,086143
199 0.088068
200 0,090024
201 0.092009
202 0,094026
203 0,096072
204 0,098150
205 0.100259
206 0.102398
207 0.104569
208 0,106772
209 0.109006
210 0.111272
211 0.113570
212 0.115899
213 0.118262
214 0.120656
215 0.123083
216 0,125542
217 0.128035
218 0.130559
219 0.133117
220 0.135708
221 0,138332
222 0,140989
223 0,143679
224 0.146403
225 0.149160
226 0,151950
227 0,154774
228 0,157632
229 0,160522
230 0,163447
231 0.166405
232 0,169396
233 0,172421
234 0,175480
235 0,178572
236 0.181698
237 0,184857
238 0.188049
239 0,191275
240 0.194534
241 0.197827
242 0.201152
243 0.204511
244 0,207902
245 0,211327
246 0.214784
247 0.218274
248 0,221796
249 0,225351
250 0,228937
251 0,232556
252 0,236207
253 0,239889
254 0.243603
255 0,247348
256 0.251124
257 0,254931
258 0,258768
259 0,262636
260 0,266534
261 0,270462
262 0,274419
263 0.278406
264 0,282422
265 0,286466
266 0,290539
267 0,294639
268 0.298768
269 0.302924
270 0.307106
271 0.311316
272 0,315551
273 0.319813
274 0,324100
275 0.328412
276 0,332749
277 0.337110
278 0,341495
279 0,345903
280 0,350334
281 0,354788
282 0,359264
283 0,363761
284 0,368279
285 0.372818
286 0,377376
287 0,381955
288 0,386552
289 0.391167
290 0.395801
291 0.400452
292 0.405119
293 0.409803
294 0,414503
295 0,419217
296 0,423946
297 0,428689
298 0,433445
299 0.438214
300 0,442995
301 0,447787
302 0,452590
303 0,457403
304 0,462226
305 0,467057
306 0,471897
307 0,476744
308 0,481599
309 0.486459
310 0,491325
311 0,496196
312 0.501070
313 0.505949
314 0,510830
315 0,515713
316 0,520598
317 0,525483
318 0,530369
319 0,535253
320 0,540137
321 0,545018
322 0,549896
323 0,554771
324 0,559642
325 0,564507
326 0,569367
327 0,574221
328 0.579067
329 0,583906
330 0,588736
331 0,593557
332 0,598368
333 0.603169
334 0.607958
335 0,612735
336 0,617500
337 0,622251
338 0,626988
339 0.631710
340 0,636417
341 0.641107
342 0,645781
343 0,650437
344 0,655075
345 0,659695
346 0,664295
347 0,668875
348 0,673434
349 0,677972
350 0,682488
351 0,686981
352 0,691451
353 0,695897
354 0.700319
355 0.704716
356 0.709088
357 0,713433
358 0,717752
359 0,722043
360 0,726307
361 0,730543
362 0,734750
363 0,738927
364 0,743075
365 0,747193
366 0,751279
367 0,755335
368 0,759359
369 0,763351
370 0,767310
371 0,771237
372 0,775130
373 0,778990
374 0,782815
375 0.786606
376 0,790363
377 0,794084
378 0,797770
379 0.801420
380 0.805034
381 0.808611
382 0.812152
383 0,815656
384 0,819123
385 0,822553
386 0,825945
387 0,829300
388 0,832616
389 0,835895
390 0,839135
391 0,842336
392 0,845499
393 0.848624
394 0,851709
395 0,854756
396 0,857764
397 0,860733
398 0,863663
399 0,866553
400 0.869405
401 0,872217
402 0,874990
403 0.877724
404 0.880419
405 0,883075
406 0,885692
407 0.888269
408 0.890808
409 0.893309
410 0,895770
411 0.898193
412 0,900578
413 0.902924
414 0,905232
415 0,907502
416 0.909734
417 0,911929
418 0,914086
419 0,916205
420 0,918288
421 0,920334
422 0,922344
423 0,924317
424 0,926254
425 0,928155
426 0,930020
427 0,931851
428 0,933646
429 0,935406
430 0,937133
431 0,938825
432 0,940483
433 0,942108
434 0,943699
435 0,945258
436 0,946785
437 0,948279
438 0,949741
439 0.951173
440 0,952573
441 0,953942
442 0,955281
443 0,956590
444 0,957870
445 0,959120
446 0,960342
447 0,961535
448 0,962701
449 0,963838
450 0,964949
451 0,966032
452 0,967090
453 0,968121
454 0,969127
455 0,970107
456 0,971063
457 0,971994
458 0,972902
459 0,973785
460 0,974646
461 0,975484
462 0,976299
463 0,977093
464 0,977865
465 0,978616
466 0,979346
467 0.980056
468 0.980746
469 0,981416
470 0,982067
471 0,982699
472 0,983313
473 0,983909
474 0,984488
475 0.985049
476 0,985593
477 0.986121
478 0,986633
479 0.987128
480 0.987609
481 0.988074
482 0.988525
483 0.988962
484 0.989384
485 0,989793
486 0,990189
487 0,990571
488 0,990941
489 0,991299
490 0,991644
491 0,991978
492 0.992301
493 0,992612
494 0,992913
495 0,993203
496 0,993483
497 0,993753
498 0.994013
499 0,994264
500 0,994506
501 0.994740
502 0,994964
503 0,995180
504 0,995389
505 0,995589
506 0,995782
507 0,995967
508 0,996146
509 0,996317
510 0,996482
511 0.996640
512 0,996793
513 0,996939
514 0,997079
515 0.997213
516 0,997343
517 0,997466
518 0,997585
519 0,997699
520 0.997808
521 0.997913
522 0.998013
523 0.998109
524 0.998200
525 0.998288
526 0,998372
527 0,998452
528 0,998529
529 0,998602
530 0,998673
531 0,998739
532 0.998803
533 0.998864
534 0.998923
535 0,998978
536 0,999031
537 0,999082
538 0.999130
539 0,999176
540 0.999219
541 0,999261
542 0.999301
543 0,999338
544 0,999374
545 0.999408
546 0,999441
547 0,999471
548 0,999501
549 0,999528
550 0.999555
551 0.999580
552 0.999604
553 0,999626
554 0,999648
555 0,999668
556 0,999687
557 0,999705
558 0,999722
559 0,999739
560 0.999754
561 0,999769
562 0,999782
563 0,999795
564 0.999808
565 0.999819
566 0.999830
567 0.999841
568 0.999851
569 0.999860
570 0.999868
571 0,999877
572 0.999884
573 0,999892
574 0,999899
575 0.999905
576 0.999911
577 0,999917
578 0,999922
579 0,999927
580 0,999932
581 0,999936
582 0.999941
583 0.999945
584 0,999948
585 0,999952
586 0,999955
587 0.999958
588 0,999961
589 0,999964
590 0,999966
591 0,999968
592 0,999971
593 0,999973
594 0,999975
595 0,999976
596 0,999978
597 0.999980
598 0,999981
599 0,999982
600 0.999984
601 0,999985
602 0,999986
603 0,999987
604 0,999988
605 0,999989
606 0.999990
607 0.999990
608 0,999991
609 0,999992
610 0,999992
611 0,999993
612 0,999994
613 0,999994
614 0,999994
615 0,999995
616 0,999995
617 0,999996
618 0,999996
619 0,999996
620 0,999997
621 0,999997
622 0,999997
623 0,999997
624 0,999998
625 0,999998
626 0,999998
627 0,999998
628 0,999998
629 0,999998
630 0,999999
631 0,999999
632 0,999999
633 0,999999
634 0,999999

Oletetaan, että jakajalla on pelimerkkejä jokaisesta nimellisarvosta, joka on tasan jaollinen yhdellä dollarilla. Ostat pelimerkkejä pöydästä 10 dollarilla. Kuinka monella eri tavalla jakaja voi antaa vaihtorahaa 10 dollarista? Entä muiden sisäänostojen summien osalta?

anonyymi

Jakaja voi jakaa 10 dollaria 42 eri tavalla. Tässä ne ovat:

10
9,1
8,2
8,1,1
7,3
7,2,1
7,1,1,1
6,4
6,3,1
6,2,2
6,2,1,1
6,1,1,1,1,1
5,5
5,4,1
5,3,2
5,3,1,1
5,2,2,1
5,2,1,1,1
5,1,1,1,1,1,1
4,4,2
4,4,1,1
4,3,3
4, 3, 2, 1
4,3,1,1,1
4,2,2,2
4,2,2,1,1
4,2,1,1,1,1,1
4,1,1,1,1,1,1,1,1
3,3,3,1
3,3,2,2
3,3,2,1,1
3,3,1,1,1,1,1
3,2,2,2,1
3,2,2,1,1,1
3,2,1,1,1,1,1,1
3,1,1,1,1,1,1,1,1,1
2,2,2,2,2,2
2,2,2,2,1,1
2,2,2,1,1,1,1,1
2,2,1,1,1,1,1,1,1,1
2,1,1,1,1,1,1,1,1,1,1,1
1,1,1,1,1,1,1,1,1,1,1,1,1

Matemaatikot kutsuvat näitä osioiksi. Tässä on osioiden lukumäärä aloitusmäärille aina 405:een asti, mikä on tietokoneeni laskeman enimmäismäärä (2^64).

Yhteinen syntymäpäivä kahdelle+ hengelle

<!--/laatikon-otsikko-->
>241
Alkuperäinen
Määrä		 Kokonais
Väliseinät
1 1
2 2
3 3
4 5
5 7
6 11
7 15
8 22
9 30
10 42
11 56
12 77
13 101
14 135
15 176
16 231
17 297
18 385
19 490
20 627
21 792
22 1002
23 1255
24 1575
25 1958
26 2436
27 3010
28 3718
29 4565
30 5604
31 6842
32 8349
33 10143
34 12310
35 14883
36 17977
37 21637
38 26015
39 31185
40 37338
41 44583
42 53174
43 63261
44 75175
45 89134
46 105558
47 124754
48 147273
49 173525
50 204226
51 239943
52 281589
53 329931
54 386155
55 451276
56 526823
57 614154
58 715220
59 831820
60 966467
61 1121505
62 1300156
63 1505499
64 1741630
65 2012558
66 2323520
67 2679689
68 3087735
69 3554345
70 4087968
71 4697205
72 5392783
73 6185689
74 7089500
75 8118264
76 9289091
77 10619863
78 12132164
79 13848650
80 15796476
81 18004327
82 20506255
83 23338469
84 26543660
85 30167357
86 34262962
87 38887673
88 44108109
89 49995925
90 56634173
91 64112359
92 72533807
93 82010177
94 92669720
95 104651419
96 118114304
97 133230930
98 150198136
99 169229875
100 190569292
101 214481126
102 241265379
103 271248950
104 304801365
105 342325709
106 384276336
107 431149389
108 483502844
109 541946240
110 607163746
111 679903203
112 761002156
113 851376628
114 952050665
115 1064144451
116 1188908248
117 1327710076
118 1482074143
119 1653668665
120 1844349560
121 2056148051
122 2291320912
123 2552338241
124 2841940500
125 3163127352
126 3519222692
127 3913864295
128 4351078600
129 4835271870
130 5371315400
131 5964539504
132 6620830889
133 7346629512
134 8149040695
135 9035836076
136 10015581680
137 11097645016
138 12292341831
139 13610949895
140 15065878135
141 16670689208
142 18440293320
143 20390982757
144 22540654445
145 24908858009
146 27517052599
147 30388671978
148 33549419497
149 37027355200
150 40853235313
151 45060624582
152 49686288421
153 54770336324
154 60356673280
155 66493182097
156 73232243759
157 80630964769
158 88751778802
159 97662728555
160 107438159466
161 118159068427
162 129913904637
163 142798995930
164 156919475295
165 172389800255
166 189334822579
167 207890420102
168 228204732751
169 250438925115
170 274768617130
171 301384802048
172 330495499613
173 362326859895
174 397125074750
175 435157697830
176 476715857290
177 522115831195
178 571701605655
179 625846753120
180 684957390936
181 749474411781
182 819876908323
183 896684817527
184 980462880430
185 1071823774337
186 1171432692373
187 1280011042268
188 1398341745571
189 1527273599625
190 1667727404093
191 1820701100652
192 1987276856363
193 2168627105469
194 2366022741845
195 2580840212973
196 2814570987591
197 3068829878530
198 3345365983698
199 3646072432125
200 3972999029388
201 4328363658647
202 4714566886083
203 5134205287973
204 5590088317495
205 6085253859260
206 6622987708040
207 7206841706490
208 7840656226137
209 8528581302375
210 9275102575355
211 10085065885767
212 10963707205259
213 11916681236278
214 12950095925895
215 14070545699287
216 15285151248481
217 16601598107914
218 18028182516671
219 19573856161145
220 21248279009367
221 23061871173849
222 25025873760111
223 27152408925615
224 29454549941750
225 31946390696157
226 34643126322519
227 37561133582570
228 40718063627362
229 44132934884255
230 47826239745920
231 51820051838712
232 56138148670947
233 60806135438329
234 65851585970275
235 71304185514919
236 77195892663512
237 83561103925871
238 90436839668817
239 97862933703585
240 105882246722733
114540884553038
242 123888443077259
243 133978259344888
244 144867692496445
245 156618412527946
246 169296722391554
247 182973889854026
248 197726516681672
249 213636919820625
250 230793554364681
251 249291451168559
252 269232701252579
253 290726957916112
254 313891991306665
255 338854264248680
256 365749566870782
257 394723676655357
258 425933084409356
259 459545750448675
260 495741934760846
261 534715062908609
262 576672674947168
263 621837416509615
264 670448123060170
265 722760953690372
266 779050629562167
267 839611730366814
268 904760108316360
269 974834369944625
270 1050197489931117
271 1131238503938606
272 1218374349844333
273 1312051800816215
274 1412749565173450
275 1520980492851175
276 1637293969337171
277 1762278433057269
278 1896564103591584
279 2040825852575075
280 2195786311682516
281 2362219145337711
282 2540952590045698
283 2732873183547535
284 2938929793929555
285 3160137867148997
286 3397584011986773
287 3652430836071053
288 3925922161489422
289 4219388528587095
290 4534253126900886
291 4872038056472084
292 5234371069753672
293 5622992691950605
294 6039763882095515
295 6486674127079088
296 6965850144195831
297 7479565078510584
298 8030248384943040
299 8620496275465025
300 9253082936723602
301 9930972392403501
302 10657331232548839
303 11435542077822104
304 12269218019229465
305 13162217895057704
306 14118662665280005
307 15142952738857194
308 16239786535829663
309 17414180133147295
310 18671488299600364
311 20017426762576945
312 21458096037352891
313 23000006655487337
314 24650106150830490
315 26415807633566326
316 28305020340996003
317 30326181989842964
318 32488293351466654
319 34800954869440830
320 37274405776748077
321 39919565526999991
322 42748078035954696
323 45772358543578028
324 49005643635237875
325 52462044228828641
326 56156602112874289
327 60105349839666544
328 64325374609114550
329 68834885946073850
330 73653287861850339
331 78801255302666615
332 84300815636225119
333 90175434980549623
334 96450110192202760
335 103151466321735325
336 110307860425292772
337 117949491546113972
338 126108517833796355
339 134819180623301520
340 144117936527873832
341 154043597379576030
342 164637479165761044d>
343 175943559810422753
344 188008647052292980
345 200882556287683159
346 214618299743286299
347 229272286871217150
348 244904537455382406
349 261578907351144125
350 279363328483702152
351 298330063062758076
352 318555973788329084
353 340122810048577428
354 363117512048110005
355 387632532919029223
356 413766180933342362
357 441622981929358437
358 471314064268398780
359 502957566506000020
360 536679070310691121
361 572612058898037559
362 610898403751884101
363 651688879997206959
364 695143713458946040
365 741433159884081684
366 790738119649411319
367 843250788562528427
368 899175348396088349
369 958728697912338045
370 1022141228367345362
371 1089657644424399782
372 1161537834849962850
373 1238057794119125085
374 1319510599727473500
375 1406207446561484054
376 1498478743590581081
377 1596675274490756791
378 1701169427975813525
379 1812356499739472950
380 1930656072350465812
381 2056513475336633805
382 2190401332423765131
383 2332821198543892336
384 2484305294265418180
385 2645418340688763701
386 2816759503217942792
387 2998964447736452194
388 3192707518433532826
389 3398704041358160275
390 3617712763867604423
391 3850538434667429186
392 4098034535626594791
393 4361106170762284114
394 4640713124699623515
395 4937873096788191655
396 5253665124416975163
397 5589233202595404488
398 5945790114707874597
399 6324621482504294325
400 6727090051741041926
401 7154640222653942321
402 7608802843339879269
403 8091200276484465581
404 8603551759348655060
405 9147679068859117602

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Kuten elokuvassa Mean Girls kysyttiin, mikä on:

anonyymi

Aloitetaan tarkastelemalla n:n (x-akseli) kuvaajaa, joka on piirretty f(n):n (y-akseli) avulla.

keskinkertaisten tyttöjen kaavio

Kuten näet, raja-arvo lähestyy ∞:tä vasemmalta ja -∞:tä oikealta. Koska se ei käänny samaan paikkaan molemmilta puolilta, raja-arvoa ei ole.

Vastataanpa kysymykseen kuitenkin ilman kuvaajaa. L'Hôpitalin sääntö sanoo, että jos f(x)/g(x):n raja = 0/0, niin lim f(x)/g(x) = lim f'(x)/g'(x). Ratkaistaan siis f'(x) ja g'(x).

f'(n) = ((ln(1 - n) - sin(n)) d/dn = -1/(1 - n) - cos(n)
g'(n) = (1 - cos 2 (n)) d/dn = sin 2 (n) d/dn

Käytetään tulolaskua ratkaistaksemme sin 2 (n) d/dn:n

sin 2 (n) d/dn = sin(n) × sin(n) d/dn =
sin(n) × cos(n) + cos(n) × sin(n) =
2sin(n)cos(n).

Ratkaistaan seuraavaksi f'(n) ja g'(n) kohdassa n = 0.

f'(0) = -1/(1-0) - cos(0) = -2.
g'(0) = 2sin(0)cos(0) = 0

Joten f'(0)/g'(0) = -2/0 = -∞. Näin ollen alkuperäisen funktion rajaa ei ole olemassa.

Haluan kehua Mean Girlsin käsikirjoittajia täydellisestä matematiikasta tässä elokuvassa. Jopa vakavasti otettavat matemaattiset elokuvat, kuten Will Hunting, usein pilaavat matematiikan täysin.

Nuori Sheldon -sarjan kolmannen kauden jaksossa 4, jonka nimi on Hobitit, fysiikka ja pallo vetoketjulla , Sheldon kysyy itseltään bingokortin mahdollisten yhdistelmien lukumäärän. Mikä on vastaus ja ovatko sarjassa esitetyt kaavat oikein?

anonyymi

Ensin käyn läpi permutaatioiden lukumäärän. Tämä tarkoittaa, että paitsi numeroilla itsellään myös niiden järjestyksellä kortilla on merkitystä. Sarakkeille B, I, G ja O on permut(15,5) = 15!/(15-5)! = 15*14*13*12*11 = 360 360 mahdollista permutaatiota. Sarakkeelle N permutaatioiden lukumäärä on permut(14,4) = 15!/(15-4)! = 15*14*13*12 = 32 760. Näin ollen bingokorttien permutaatioiden kokonaismäärä on 360 360 4 × 32 760 = 552446474061128648601600000.

Toiseksi käyn läpi yhdistelmien lukumäärän. Tämä tarkoittaa, että numeroilla on merkitystä, mutta ei niiden järjestyksellä kortilla. Sarakkeissa B, I, G ja O on combin(15,5) = 15!/(5!*(15-5)!) = (15*14*13*12*11)/(1*2*3*4*5) = 3 003 mahdollista yhdistelmää. Sarakkeessa N permutaatioiden lukumäärä on combin(14,4) = 15!/(4!*(15-4)!) = (15*14*13*12)/(1*2*3*4) = 1 365. Näin ollen bingokorttien permutaatioiden kokonaismäärä on 3 003 4 × 1 365 = 111007923832370565.

ys1

ys2

Sarjassa Sheldon kysyy itseltään, miten AINUTLAATUISIA bingokortteja voi olla olemassa. Myöhempien virheellisten kaavojen perusteella oletan hänen tarkoittavan permutaatioita. Toisin sanoen kaksi korttia, joissa on samat numerot mutta eri paikoissa, olisivat molemmat ainutlaatuisia.

Nuori Sheldon Bingo 3

Yllä oleva kuva näyttää Sheldonin kaavan B-, I-, G- ja O-sarakkeille. Hän saa aluksi kaavan oikein kohdassa 5! × combin(15,5). Hän kuitenkin sieventää sen virheellisesti muotoon 15!/(15!-5)!. Toisen huutomerkin ei pitäisi olla siinä. Sen pitäisi lukea 15!/(15-10)!. Sitten hän kuitenkin palaa oikeaan vastaukseen kohdassa 360 360.

Nuori Sheldon Bingo 4

Meillä on täsmälleen sama ongelma N-sarakkeen kanssa. Kaavan pitäisi olla 15!/(15-4)!, ei 15!/(15!-4)!. Toinen huutomerkki pilaa sen.

Ironista kyllä, myöhemmin jaksossa Sheldonista tulee pakkomielteinen kiinnostus Taru sormusten herrasta -elokuvan kronologian virheisiin, aivan kuten minäkin olen pakkomielteinen tästä.

Nuori Sheldon Bingo 4

Täysi 100 litran säiliö sisältää vettä ja 10 kg suolaa. Jos lisäämme 10 litraa puhdasta vettä minuutissa ja samanaikaisesti tyhjennämme 10 litraa liuosta minuutissa, kuinka paljon suolaa säiliöön jää 30 minuutin kuluttua?

Ace2

Aloitetaan määrittelemällä pari muuttujaa:

  • s = säiliössä olevan suolan määrä kg
  • t = minuuttia siitä, kun suola kaadettiin säiliöön

Meille annetaan, että 10 % suolasta valuu pois minuutissa. Matemaattisesti ilmaistuna:

ds/dt = (-10/100) × s

Järjestetäänpä se uudelleen muotoon:

ds = (-10/100) × s dt

-10/s ds = dt

Molempien puolien integrointi:

(1) -10 × ln(s) = t + c

Seuraavaksi etsitään pelätty integrointivakio. Tätä varten meille annetaan, että s = 10, kun t = 0. Yhdistämällä se yllä olevaan kaavaan (1) saadaan:

-10 × ln(10) = 0 + c

Joten c = -10 × ln(10)

Laittamalla se yhtälöön (1) saadaan:

(2) -10 × ln(s) = t -10 × ln(10)

Käsillä oleva kysymys on, kuinka paljon suolaa säiliössä on hetkellä t=30. Ratkaise s, kun t=30:

-10×ln(s) = 30 -10×ln(10). Jaa seuraavaksi molemmat puolet luvulla -10...

ln(s) = -3 + ln(10)

s = exp(-3 + ln(10))

s = exp(-3) × exp(ln(10))

s = exp(-3) × 10

s = ~ 0,4979 kg suolaa.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Oletetaan, että suurempi kuvio on neliö, niin mikä on x:n pinta-ala?

Dyana alkaen Las Vegas

Tällaisten ongelmien avain on niiden asettelussa. Suosittelen yrittämään tiivistää ongelman mahdollisimman vähään tuntemattomaan. Tässä tapauksessa voimme ilmaista tuntemattomat etäisyydet neliöllä vain kolmeksi seuraavasti:

neljä kolmiota neliöratkaisussa

Suorakulmioiden käsittely on helpompaa kuin kolmioiden. Koska tiedämme kolmen kolmion pinta-alan, voimme kaksinkertaistaa koon ja pinta-alan. Se antaa meille:

  • noin = 10
  • ac=16
  • (ab)(ac)=14

Jaetaan tekijöihin (ab)(ac):

a 2 - ab - ac + bc = 14

a 2 - 10 - 16 + bc = 14

(1) a² + bc = 40

Ilmaistaan b ja c muuttujan a avulla, jotta saadaan tämä yhteen muuttujaan:

b = 10/a

c = 16/a

Sijoittamalla b ja c näillä arvoilla yhtälöön (1):

2 + (10/a)*(16/a) = 40

a² + 160 / a² = 18

Seuraavaksi poistetaan nimittäjässä oleva 2 kertomalla kaikki luvulla 2 .

4 + 160 = 40 * 2

4–40 * 2 + 160 = 0

Määritellään uusi muuttuja y = a 2

v 2 - 18 v + 32 = 0

Ratkaistaan seuraavaksi y käyttämällä toisen asteen kaavaa:

y = (40 +/- neliöjuuri(1600-640))/2

y = (40 +/- neliöjuuri(960))/2

y = (40 +/- 8 * neliöjuuri(15))/2

y = 20 +/- 4*neliömetriä(15)

Koko neliön pinta-ala on a2 , joka on kätevästi yhtä suuri kuin y. Yllä olevan yhtälön mukaan, jos +/- on negatiivinen, niin y = apx 4,5081, mikä on ilmeisen väärin, koska tiedämme pinta-alan olevan vähintään 20, edes x:ää lukuun ottamatta. Joten neliön pinta-alan on oltava 20 + 4*sqrt(15).

Kolmen annetun kolmion pinta-ala on 5 + 7 + 8 = 20. Vähentämällä tämä neliön kokonaispinta-alasta saadaan x:n pinta-ala: 20 + 4 * sqrt(15) - 20 = 4 * sqrt(15) = appx 15,4919.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

aurinkorannikko

Huomaa t-paitani tässä kuvassa. Elokuvateatterin kassa kehui sitä, kun menin katsomaan elokuvaa Uncut Gems . Kiitin häntä kiduttamalla häntä tällä tehtävällä, mutta käyttäen vain kolmioita, joiden pinta-alat ovat 2, 3 ja 4. Elokuvan jälkeen tarkistin hänen vointinsa, eikä hän ollut vieläkään ratkaissut tehtävää, mutta näytti yrittävän. Niinpä kirjoitin hänelle seuraavan ratkaisun Suncoast-baarissa. Hän itse asiassa näytti arvostavan sitä. Uskon, että tuo nuori nainen pääsee pitkälle elämässä.

Neliönmuotoinen tikkataulu, jonka mitat ovat 1 kertaa 1, heitetään siihen siten, että se voi osua mihin tahansa yhtä todennäköisesti. Olkoot pisteen ja pisteen koordinaatit (x,y), jossa sekä x että y ovat tasaisesti ja toisistaan riippumatta jakautuneet välillä 0–1.

Olkoon z = round(x/y). Toisin sanoen, z = x/y, pyöristettynä lähimpään kokonaislukuun. Mikä on todennäköisyys sille, että z on parillinen luku?

anonyymi

Seuraavasta vihjeestä on erittäin hyödyllistä tietää ääretön sarja.

Leibnizin kaava π: lle toteaa:

1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... = π/4

Vain vastauksen saat napsauttamalla seuraavaa painiketta.

[spoileri=Vastaus](5 - π)/4 = apx. 0,464601836602552. [/spoiler]

Napsauta alla olevaa painiketta nähdäksesi ratkaisun.

Jos x/y < 0,5, suhde pyöristyy n:stä alaspäin nollaan ja parilliseen lukuun. Mikä tahansa tikkataulun piste (0,0) ja (0,5) muodostaman suoran vasemmalla puolella pyöristyy alaspäin nollaan. Tuo pinta-ala on suorakulmainen kolmio, jonka sivu on 1 ja 1/2. Muista, että kolmion pinta-ala on (1/2) * pohja * korkeus. Näin ollen näiden pisteiden pinta-ala pyöristettynä alaspäin nollaksi on (1/2) * (1/2) = 1/4.

Seuraavaksi kaavion alue, joka pyöristyy seuraavaan parilliseen lukuun, 2, on tilanne, jossa 1,5 < x/y < 2,5. Tämä alue on kolmio, jonka kanta on 2/3 - 2/5 ja korkeus 1. Huomaa, että nämä ovat x/y-luvun rajojen käänteislukuja, koska x on yhtä kuin 1, joten meidän on käännettävä y. Joten alue, joka pyöristyy lukuun 2, on (1/2)*(2/3 - 2/5).

Seuraavaksi seuraavaan parilliseen lukuun, 4, pyöristettävä alue kaaviossa on silloin, kun 3,5 < x/y < 4,5. Tämä alue on kolmio, jonka kanta on 2/7 - 2/9 ja korkeus 1. Joten lukuun 2 pyöristettävä alue on (1/2) * (2/7 - 2/9).

Seuraavaksi seuraavaan parilliseen lukuun, 6, pyöristettävä alue kaaviossa on silloin, kun 5,5 < x/y < 6,5. Tämä alue on kolmio, jonka kanta on 2/11 - 2/13 ja korkeus 1. Joten lukuun 2 pyöristettävä alue on (1/2) * (2/11 - 2/13).

Alatko nähdä kaavaa? Se kuuluu:

1/4 + 1/2 * (2/3 - 2/5 + 2/7 - 2/9 + 2/11 - 2/13 + ... ) =

1/4 + (1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ...) =

Siirretään -1 noiden sulkujen sisään.

5/4 + (-1 + 1/3 - 1/5 + 1/7 - 1/9 + 1/11 - 1/13 + ...) =

5/4 - (1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 + ...) =

Seuraavaksi, muistakaa yllä oleva vinkkimme:

1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11

Palatakseni käsillä olevaan kysymykseen...

5/4 - π/4 =

(5 - π) / 4 = apx. 0,464601836602552.

Onpa mielenkiintoista, miten π ja e esiintyvät matematiikassa joka puolella.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Olkoon 9 × + 12 × = 16 ×

Mikä on x?

anonyymi

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

x = [ln(1 + neliöjäännös(5)) - ln(2)] / [ln(4) - ln(3)] = apk. 1.67272093446233.

Napsauta alla olevaa painiketta nähdäksesi ratkaisun.

9 × + 12 × = 16 × =

Jaa molemmat puolet luvulla 9 x

1 + (12/9) × = (16/9) ×

1 + (4/3) × = ((4/3) × ) ²

(1) Olkoon u = (4/3) x

1 + u = u2

Toisen asteen kaavan mukaan...

u = (1 + neliöjuuri(5)) / 2 (kultainen leikkaus)

Laitetaan se takaisin yhtälöön (1):

(4/3) x = (1 + neliöjuuri(5)) / 2

Ota molempien puolien lokitiedot:

x ln(4/3) = ln[(1 + neliö(5)) / 2]

x = ln[(1 + neliöjuuri(5)) / 2] / ln(4/3)

x = [ln(1 + neliöjuuri(5) - ln(2)] / [ln(4) - ln(3)] = appx. 1.67272093446233.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Kuittaus: Sain tämän ongelman muunnelman Presh Talwalkarilta Mind Your Decisions -sivustolta.

Maanviljelijä kylvää viisi omenansiementä. Joka päivä jokaisella siemenellä on 1/3 mahdollisuus itää. Mikä on keskimääräinen aika, kunnes kaikki viisi puuta itävät?

anonyymi

Vastaus on noin 6,131415853 päivää.

Maanviljelijä kylvää viisi omenansiementä. Joka päivä jokaisella siemenellä on 1/3 mahdollisuus itää. Mikä on keskimääräinen aika, kunnes kaikki viisi puuta itävät?

Lasketaanpa asiaa aivan takaperin. Jos jäljellä on yksi itämätön siemen, sen itäminen kestää keskimäärin 1/p päivää, missä p on itämisen todennäköisyys minä tahansa päivänä. Koska p = 1/3, itäminen kestää keskimäärin 3 päivää. Kutsutaan tätä t 1 = 3:ksi.

Entä jos jäljellä on kaksi siementä? On ap 2 = 1/9 mahdollisuus, että molemmat itävät seuraavana päivänä, ja olemme valmiita. Todennäköisyys sille, että toinen itää seuraavana päivänä, on 2 × p × q, jossa q on todennäköisyys, ettei itäisi. Näin ollen yhden siemenen itämisen todennäköisyys on 2 × (1/3) (2/3) = 4/9. Todennäköisyys sille, ettei kumpikaan siemen itäisi, on q 2 = (2/3) 2 = 4/9. Kutsutaan kahden siemenen odotettua päivien lukumäärää t 2 .

t² = 1 + (4/9) × t¹ + (4/9) t²

t² = (1 - (4/9)) = 1 + (4/9) × t¹

t2 = (1 + (4/9) × 3) / (1 - (4/9))

t2 = (21/9) / (5/9)

t2 = (21/9) × (9/5) = 21/5 = 4,2

Entä jos jäljellä on kolme siementä? On ap 3 = 1/27 todennäköisyys, että kaikki itävät seuraavana päivänä, ja olemme valmiita. Todennäköisyys sille, että yksi siemen itää seuraavana päivänä, on 3×p×q 2 = 3×(1/3)(2/3) 2 = 12/27. Todennäköisyys sille, että kaksi siementä itää seuraavana päivänä, on 3×p 2 × q = 3×(1/3) 2 ×(2/3) = 6/27. Todennäköisyys sille, ettei yhtään siementä itäisi, on q 3 = (2/3) 3 = 8/27. Kutsutaan kolmen siemenen odotettua lukumäärää t 3:ksi .

t³ = 1 + (6/27) ⁻¹ + (12/27)× t² + (8/27)× t³

t³ = 1 + (6/27) × 3 + (12/27) × 4,2 + (8/27) × t³

t3 × (1 - 8/27) = (1 + 18/27 + 28/15)

t3 = (1 + 18/27 + 28/15) / (1 - 8/27) = 477/95 = noin 5,02105263

Entä jos jäljellä on neljä siementä? On ap 4 = 1/81 mahdollisuus, että kaikki neljä itävät seuraavana päivänä, ja olemme valmiita. Todennäköisyys sille, että yksi siemen itää seuraavana päivänä, on 4 × p × q 3 = 4 × (1/3) (2/3) 3 = 32/81. Todennäköisyys sille, että kaksi siementä itää seuraavana päivänä, on combin(4,2) × p 2 × q 2 = 6 × (1/3) 2 × (2/3) 2 = 24/81. Todennäköisyys sille, että kolme siementä itää seuraavana päivänä, on combin(4,3) × p 3 × q = 4 × (1/3) 3 × (2/3) = 8/81. Todennäköisyys sille, että yhtään siementä ei itäisi, on q 4 = (2/3) 4 = 16/81. Kutsutaan kolmen siemenen päivien odotettua lukumäärää t 4:ksi .

t4 = 1 + (8/81) × t1 + (24/81) × t2 + (32/81) × t3 + (16/81) × t4

t4 = 1 + (8/81)×3 + (24/81)×4,2 + (32/81)×5,02105263 + (16/81)× t4

t4 = (1 + (8/81)×3 + (24/81)×4,2 + (32/81)×5,02105263) / (1 - (16/81))

t4 = noin 5,638056680161943319838056680.

Entä jos kaikki viisi siementä on jäljellä? On ap 5 = 1/243 todennäköisyys sille, että kaikki viisi itävät seuraavana päivänä, ja olemme valmiita. Todennäköisyys sille, että yksi siemen itää seuraavana päivänä, on 5 × p × q 4 = 5 × (1/3) (2/3) 4 = 80/243. Todennäköisyys sille, että kaksi siementä itää seuraavana päivänä, on combin(5,2) × p 2 × q 3 = 10 × (1/3) 2 × (2/3) 3 = 80/243. Todennäköisyys sille, että kolme siementä itää seuraavana päivänä, on combin(5,3) × p 3 × q = 10 × (1/3) 3 × (2/3) 2 = 40/243. Todennäköisyys sille, että neljä siementä itää seuraavana päivänä, on combin(5,4) × p 4 × q = 5 × (1/3) 4 × (2/3) = 10/243. Siementen itämättömyyden todennäköisyys on q 5 = (2/3) 5 = 32/243. Kutsutaan odotettua päivien lukumäärää kolmella siemenellä t 5:ksi .

t5 = 1 + (10/243)× t1 + (40/243)× t2 + (80/81)× t3 + (80/243)× t4 + (32/243)× t5

t5 = (1 + (10/243) × t1 + (40/243) × t2 + (80/81) × t3 + (80/243) × t4 ) / (1 - (32/243))

t5 = (1 + (10/243)×3 + (40/243)×4,2 + (80/243)×(477/95) + (80/243)×5,63805668) / (1 - (32/243))

t 5 = noin 6,131415853.

Tämä tehtävä on mukaelma Presh Talwalkarin Mind Your Decisions -kirjan samankaltaisesta tehtävästä.

Minulla on kaksiosainen kysymys.

Osalle 1 annettu:
  • x + y + z = 1
  • x^2 + y^2 + z^2 = 4
  • x^3 + y^3 + z^3 = 9

Mikä on x^4 + y^4 + z^4?

Toisen osan osalta, mikä on vastaus yleiseen tapaukseen, kun:

  • x + y + z = a
  • x^2 + y^2 + z^2 = b
  • x^3 + y^3 + z^3 = c

anonyymi

Kysymys 1: 97/6 = noin 16,166666

Kysymys 2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2

Katso ratkaisuni (PDF)

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Mikrobi, kutsutaanpa sitä Covid-20:ksi, voi synnyttää uuden mikrobin milloin tahansa. Todennäköisyys sille, että tietty mikrobi syntyy tiettynä ajankohtana tietystä emomikrobista, on aina sama riippumatta siitä, kuinka kauan edellisestä kutemisesta on kulunut. Keskimääräinen aika saman mikrobin kutemisen välillä on yksi päivä. Matemaattisesti ilmaistuna saman mikrobin odotettu kutemisen välinen aika noudattaa eksponentiaalista jakaumaa, jonka keskiarvo on yksi päivä.

Kun mikrobi pääsee keuhkoihisi, kuinka monta mikrobia sinulla on odotettavissa seitsemän päivän kuluttua?

anonyymi

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

Vastaus on e 7 = noin 1 096,6332.

Napsauta alla olevaa painiketta nähdäksesi ratkaisun.

Tämä ratkaisu vaatii tavallisen differentiaaliyhtälön. Jos et ole vielä siinä vaiheessa matematiikan opintojasi, et tule ymmärtämään sitä.

Olkoon:
m = Covid-20-mikrobien lukumäärä
t = aika päivinä

Koska jokainen mikrobi tuottaa keskimäärin uuden mikrobin kerran päivässä, m mikrobia tuottaa keskimäärin m uutta mikrobia päivässä. Toisin sanoen mikrobien lisääntymisnopeus (m) millä tahansa ajanhetkellä t voidaan kirjoittaa muodossa:

dm/dt = m.

En ole varma oikeasta tavasta ilmaista tämä, mutta erota dt oikealle puolelle:

dm = m dt.

Jaa molemmat puolet m:llä:

1/m² dm = 1 dt.

Yhdistä molemmat puolet:

ln(m) = t + C, jossa C on integrointivakio.

Meille on annettu, että hetkellä 0 on yksi mikrobi. Toisin sanoen, kun t = 0, m = 1. Voimme sijoittaa nämä arvot yllä olevaan yhtälöön ratkaistaksemme C:n:

ln(1) = 0 + C

0 = 0 + C

C = 0.

Meillä on nyt ln(m) = t.

Ota molempien puolien exp():

m = e t

Joten hetkellä t=7 mikrobien lukumäärä on e7 = noin 1096,6332.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Vanhassa lännen saluunassa korttipelistä käyty riita kärjistyi niin, että kaikki lähistöllä olevat cowboyt vetivät aseensa ja ampuivat toisiaan.

Kun savu viimein hälveni, 90 % cowboyista oli ammuttu jalkaan, 85 % käsivarteen, 80 % vatsaan ja 75 % päähän. Yllättäen vain ne cowboyt, jotka saivat kaikkia neljää haavatyyppiä, kuolivat suuressa tulitaistelussa.

Mikä on pienin mahdollinen prosenttiosuus cowboyista, jotka lopulta haudattiin?

Gialmere

30%

Ammu ensin 90% cowboyista jalkaan.

Ammu seuraavaksi 10 % jäljellä olevista pystyssä olevista käsivarteen. Sinulla on vielä 75 % ammuttavana käsivarteen, joten ota ne niistä, jotka on jo ammuttu jalkaan.

Eli nyt olemme tilanteessa:

Vain jalka 15 % (90 % - 75 %)
Vain 10 % varusteet
Molemmat 75%
Kumpikaan 0%

Kokonaisosuus: 90 %
Kokonaisvarsi: 85 %

Seuraavaksi siirrytään vatsavammoihin (80 %). Ammutaan ne 25 %, joilla on vain yksi vatsavamma. Meillä on 80–25 % = 55 % enemmän ihmisiä ammuttavana. Otamme nuo 55 % molemmilla vammoilla olevien ihmisten joukosta. Eli nyt olemme tilanteessa:

Jalka ja suolisto 15%
Käsivarsi ja vatsa 10%
Jalka ja käsivarsi 20 % (75 % - 55 %)
Kaikki kolme 55 %
Yksi loukkaantuminen 0%
Nolla loukkaantumista 0%

Lopuksi, tarkastellaan niitä 75 %:a, joilla on päävammoja. Ensin ammutaan ne 45 %, joilla on tasan kaksi vammaa. Meillä on vielä 30 % jäljellä, joten ne otetaan niistä 55 %:sta, joilla on kaikki kolme vammaa. Jäljelle jää:

Pää, jalka ja suolisto 15%
Pää, käsivarsi ja vatsa 10%
Pää, jalka ja käsivarsi 20%
Jalka, käsivarsi ja suolisto: 25 % (55 % - 30 %)
Kaikki neljä 30%
Nolla loukkaantumista 0%
Yksi loukkaantuminen 0%
Kaksi loukkaantumista 0%

Olkoon cowboyita 20. Valitsemme tämän luvun, koska kaikki todennäköisyydet ovat tasan jaollisia 5 prosentilla ja 5 % luvusta 20 on 1.

Asettele ne riviin. Aloita vasemmasta ja ammu niistä 90 % eli 18 jalkaan. Tee sitten kaavio, jossa cowboy-numero on ylimmässä rivissä ja kunkin vammamäärä vasemmassa sarakkeessa seuraavasti.

Vamma 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L L
2
3
4
Kokonais 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0

Seuraavaksi sinun täytyy ampua 85 % osumalla eli 17 osumaa käsivarteen. Aloita kahdesta cowboysta, joita ei ammuttu jalkaan. Sinulla on vielä 15 osumaa jäljellä. Palaa vasemmalla olevan cowboyn luo ja liiku riviä alaspäin ampuen yhteensä 15 jo ammuttua osumaa jalkaan. Loukkaantumiskorttisi pitäisi näyttää tältä:

Vamma 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L L A A
2 A A A A A A A A A A A A A A A
3
4
Kokonais 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1

Seuraavaksi sinun täytyy ampua 80 % osumalla eli 16 vatsaan. Aloita VIIDELLÄ cowboylla, joilla on vain yksi vamma. Sinulla on vielä 11 jäljellä. Palaa vasemmalla olevan cowboyn luo ja liiku riviä alaspäin ampuen yhteensä 11 kahdesti ammuttua osumaa. Loukkaantumiskorttisi pitäisi näyttää tältä:

Vamma 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L L A A
2 A A A A A A A A A A A A A A A G G G G G
3 G G G G G G G G G G G
4
Kokonais 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2

Seuraavaksi sinun täytyy ampua 75 % osumalla eli 15 osumaa päähän. Aloita yhdeksällä cowboylla, jotka ammuttiin vain kahdesti. Sinulla on vielä kuusi jäljellä. Palaa vasemmalla olevan cowboyn luo ja liiku riviä alaspäin ampuen yhteensä kuusi jo kolme kertaa ammuttua cowboyta. Loukkaantumiskorttisi pitäisi näyttää tältä:

Vamma 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 L L L L L L L L L L L L L L L L L L A A
2 A A A A A A A A A A A A A A A G G G G G
3 G G G G G G G G G G G H H H H H H H H H
4 H H H H H H
Kokonais 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3

Kuten näette, kuutta cowboyta on ammuttu neljä kertaa ja neljäätoista kolme kertaa. Näin ollen korkein prosenttiosuus, joka voi saada vain kolme vammaa, on 14/20 = 70 %.

Yleisessä tapauksessa, jos neljä todennäköisyyttä ovat a, b, c ja d, niin suurin mahdollinen suhdeluku on 1-(a+b+c+d), kunhan a+b+c+d >=3 ja a+b+c+d <=4.

Haluan kiittää ja antaa tunnustusta Wizard of Vegas -foorumin jäsenelle CharliePatrickille tästä ratkaisusta.

Tätä kysymystä kysytään ja siitä keskustellaan foorumillani, tästä viestistä alkaen.

Sammakko voi hypätä 30 senttimetriä tai 60 senttimetriä. Sammakko hyppää yhteensä tasan kymmenen jalkaa useiden hyppyjen aikana, aina eteenpäin. Kuinka monella eri tavalla tämä voidaan tehdä ottaen huomioon sekä hyppymatkan että -järjestyksen?

anonyymi

89

  1. Jos sammakon tarvitsee hypätä vain yhden jalan verran, on ilmiselvästi vain yksi tie. Muista, että sammakko ei voi yliampua tavoitteestaan.
  2. Jos sammakon täytyy hypätä kaksi jalkaa, on kaksi tapaa tehdä se – (1) 1 jalka ja 1 jalka tai (2) 2 jalkaa.

    3. Jos sammakon täytyy hypätä metrin matka, se voi olla joko 30 senttimetriä tai 60 senttimetriä päässä ennen viimeistä hyppyä. On yksi tapa olla kahden jalan päässä, kuten vaiheessa 1 on esitetty, ja kaksi tapaa olla yhden jalan päässä, kuten vaiheessa 2 on esitetty. Näin ollen on kolme tapaa hypätä kolmen jalan päähän. Tämä on myös helposti todennettavissa muodossa (1) 1+1+1, (2) 1+2, (3) 2+1.

    Jos sammakon täytyy hypätä 1,2 metriä, se voi olla joko 60 tai 90 metrin päässä ennen viimeistä hyppyä. 2 jalan päässä voi olla kaksi tapaa, kuten vaiheessa 2 on esitetty, ja 30 senttimetrin päässä voi olla kolme tapaa, kuten vaiheessa 3 on esitetty. Näin ollen 1,2 metrin päässä voi hypätä viisi tapaa. Tämä on myös helposti todennettavissa seuraavasti: (1) 1+1+1+1, (2) 1+1+2, (3) 1+2+1, (4) 2+1+1, (5) 2+2.

    Jos sammakon täytyy hypätä 1,5 metriä, se voi olla joko 0,9 metrin tai 1,2 metrin päässä ennen viimeistä hyppyä. 2 jalan päässä voi olla kolme tapaa, kuten vaiheessa 3 on esitetty, ja 1 jalan päässä voi olla viisi tapaa, kuten vaiheessa 4 on esitetty. Näin ollen 1,5 metrin päässä voi hypätä 3 + 5 = 8 tapaa. Tämä on myös helppo varmistaa seuraavasti: (1) 1 + 1 + 1 + 1 + 1, (2) 1 + 1 + 1 + 2, (3) 1 + 1 + 2 + 1, (4) 1 + 2 + 1 + 1, (5) 2 + 1 + 1 + 1, (6) 2 + 2 + 1, (7) 2 + 1 + 2, (8) 1 + 2 + 2.

    Alatko nähdä kaavaa? Se on Fibonaccin lukujono. Samalla logiikalla jatkaen sammakko voi hypätä yhteensä tasan kolme metriä 89 eri tavalla.

Käyttämällä Yhdysvaltain standardikolikoita (1, 5, 10, 25, 50 senttiä ja 1 dollari), kuinka monella tavalla voi vaihtorahaa 1 dollarista?

Gialmere

Vastaus on 293.

Olkoon a(x) = x sentin ansaitsemistapojen lukumäärä käyttäen vain pennejä ja nikkeleitä, missä x on jaollinen viidellä.

a(x) = 1 + (x/5)

Toisin sanoen tapojen lukumäärä on muutoksen mahdollisten nikkelien lukumäärä, joka vaihtelee välillä 0 - x/5.

Olkoon b(x) = x sentin ansaitsemistapojen lukumäärä käyttäen vain pennejä, nikkeleitä ja dimejä, missä x on jaollinen viidellä.

b(0)=1
b(5)=2
b(x) = a(x) + b(x-10), missä x > = 10.

Yksinkertaisesti sanottuna tapojen lukumäärä x sentin ansaitsemiseksi on summa (1) b(x-10) = tapojen lukumäärä x-10 sentin ansaitsemiseksi lisäämällä jokaiseen tapaan 10 desimillionin ja (2) a(x) = tapojen lukumäärä ilman 10 desimillionin kolikoita.

Olkoon c(x) = x sentin ansaitsemistapojen lukumäärä käyttäen vain pennejä, nikkeleitä, dimejä ja neljänneskolikkoja, missä x on jaollinen luvulla 25.

c(0) = 1
c(x) = b(x) + c(x-25), missä x > = 25.

Yksinkertaisesti sanottuna tapojen lukumäärä x sentin ansaitsemiseksi on summa (1) c(x-25) = tapojen lukumäärä x-25 sentin ansaitsemiseksi lisäämällä jokaiseen tapaan yksi neljänneskolikko ja (2) b(x) = tapojen lukumäärä ilman neljänneskolikkoja.

Olkoon d(x) = tapojen lukumäärä x sentin ansaitsemiseksi käyttäen vain pennejä, nikkeleitä, dimejä, neljännesdollareita ja puolta dollaria, missä x on jaollinen luvulla 50.

d(0) = 1
d(x) = c(x) + d(x-50), missä x > = 50.

Yksinkertaisesti sanottuna tapojen lukumäärä x sentin ansaitsemiseksi on summa (1) d(x-50) = tapojen lukumäärä, joilla saadaan x-50 senttiä lisäämällä puoli dollaria jokaiseen tapaan ja (2) c(x) = tapojen lukumäärä ilman puolta dollaria.

Seuraavassa taulukossa näkyvät nämä arvot välillä x = 5–100.

Muutoksen tekemisen tapoja

x kirves) b(x) c(x) d(x)
0 1 1 1
5 2 2 0
10 3 4 0
15 4 6 0
20 5 9 0
25 6 12 13
30 7 16 0
35 8 20 0
40 9 25 0
45 10 30 0
50 11 36 49 50
55 12 42 0
60 13 49 0
65 14 56 0
70 15 64 0
75 16 72 121
80 17 81 0
85 18 90 0
90 19 100 0
95 20 110 0
100 21 121 242 292

Lopuksi lisää yksi dollarin kolikkoa kohden ja vastaus on 292 + 1 = 293.

Tätä kysymystä on käsitelty foorumillani Wizard of Vegasissa .

Lamppuja on äärettömän paljon, ja ne kaikki ovat sammutettuja. Aika lamppujen sytyttämisen välillä noudattaa eksponentiaalista jakaumaa*, jonka keskiarvo on yksi päivä. Kun lamppu on syttynyt, sen käyttöikä noudattaa myös eksponentiaalista jakaumaa, jonka keskiarvo on yksi päivä.

Kuinka kauan keskimäärin kestää, kunnes ensimmäinen lamppu palaa?

*: Eksponentiaalista jakaumaa noudattavilla satunnaisilla tapahtumilla ei ole muistia, koska menneisyydellä ei ole merkitystä. Toisin sanoen yksittäinen tapahtuma ei ole koskaan myöhässä ja sen todennäköisyys on aina sama.

Ace2

Vastaus on e - 1 = apx. 1.7182818...

Ensimmäisen lampun syttyminen kestää keskimäärin yhden päivän.

Siitä kestää keskimäärin puoli päivää seuraavaan merkittävään tapahtumaan, joka on joko uuden lampun sytyttäminen tai ensimmäisen lampun palaminen. Lisäämme odotusaikaan puoli päivää kyseiseen tapahtumaan asti. Joten olemme nyt 1 + (1/2) = 1,5 päivää.

On puolet todennäköisyyttä, että toinen tapahtuma oli toisen lampun sytyttäminen. Tässä tapauksessa on 1/3 päivän odotusaika seuraavaan merkittävään tapahtumaan (joko toisen kahdesta ensimmäisestä lampusta palaminen tai uuden lampun sytyttäminen). Lisää siis odotusaikaan 1/2:n (todennäköisyys päästä tähän pisteeseen) ja 1/3:n tulo, joka on 1/6. Eli emme ole enää 1,5 + 1/6 = 5/3 = 1,66667 päivää.

On (1/2)*(1/3) = 1/6 todennäköisyys, että kolmas merkittävä tapahtuma oli kolmannen lampun sytyttäminen. Tässä tapauksessa on 1/4 päivän odotusaika seuraavaan merkittävään tapahtumaan (joko yhden kolmesta ensimmäisestä lampusta palaminen tai uuden lampun sytyttäminen). Lisää siis odotusaikaan 1/6:n (todennäköisyys päästä tähän pisteeseen) ja 1/4:n tulo, joka on 1/24. Eli emme ole enää 5/3 + 1/24 = 41/24 = 1,7083 päivää.

Tämän kaavan mukaisesti vastaus on (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...

Yleisesti tiedetään, että e = (1/0!) + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + ...

Ainoa ero on, että vastauksestamme puuttuu 1/0!-tekijä. Näin ollen vastaus on e - 1/0! = e - 1 = appx. 1.7182818...

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

A, B, C ja D ovat kaikki eri positiivisia kokonaislukuja.

A < B < C < D

Etsi suurin D siten, että

1/A + 1/B + 1/C + 1/D = 1

Gialmere

Vastaus on 42. A, B ja C ovat 2, 3 ja 7.

1/2 + 1/3 + 1/7 + 1/42 = 1.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Katsottuani läpi The Queen's Gambitin huomasin, ettei yksikään ohjelman peleistä päättynyt tasapeliin. Luulin, että shakissa korkeilla tasoilla on paljon tasapelejä. Kuinka monta prosenttia peleistä päättyy tasapeliin suurmestaritason shakissa?

anonyymi

ChessBase.com-sivuston artikkelin Has the number of draws in shacks increased? mukaan kirjoittaja Qiyu Zhou toteaa, että 78 468:ssa pistemäärältään 2600 tai sitä korkeamman pistemäärän (suurmestariksi vaaditaan 2500 pistettä) pelatussa pelissä tulokset olivat seuraavat:

  • Musta voittaa: 18,0 %
  • Valkoiset voittavat: 28,9 %
  • Tasapeli: 53,1 %

Pelilaudassa on 5x5 kokoinen tapin muotoinen alue ja kolme tappia. Mikä on todennäköisyys, että kolme satunnaisesti asetettua tappia muodostaa kolmion?

anonyymi

93,39 %

Ensinnäkin, tapuille on combin(25,3) = 2 300 mahdollista yhdistelmää.

Kuinka moni näistä yhdistelmistä muodostaa kolmion? Käytetään tätä lautaa apuna:

reikätaulu

Ensinnäkin on viisi riviä, viisi saraketta ja kaksi lävistäjää. Jokaiselle niistä on combin(5,3) = 10 tapaa sijoittaa tapit riviin. Joten kombinaatioita on 12 * 10 = 120 tällä tavalla.

Toiseksi, rivin/sarakkeen keskimmäisen neliön voi yhdistää viereisen rivin/sarakkeen keskimmäiseen neliöön neljällä eri tavalla. Toisin sanoen, nämä kolme sijoittelua:

  • A3, B4, C5
  • C5, D4, E3
  • E3, D2, C1
  • C1, B2, A3

Joten nyt olemme luvussa 120 + 4 = 124

Kolmanneksi, on neljä erilaista diagonaaliviivaa, jotka ovat neljä välilyöntiä:

  • A2, B3, C4, D5
  • B5, C4, D3, E2
  • E4, D3, C2, B1
  • D1, C2, B3, A4

Jokaiselle niistä on combin(4,3)=4 tapaa sijoittaa kolme tappia. Eli lisää tulee 4*4 = 16 lisää.

Olemme nyt luvussa 124 + 16 = 140

Neljänneksi, tarkastellaan ratsun liikkumista shakissa 2x1 L-muodossa. Jokaista kulmaa kohden on kaksi tapaa, joilla ratsu voi liikkua. Kaikissa näissä tapauksissa ratsu voi liikkua uudelleen samaa linjaa pitkin, josta se lähti ensimmäiselle siirrolle. Eli 4 * 2 = 8 lisää:

  • A1, C2, E3 A1, B3, C5
  • A5, B3, C1
  • A5, C4, E3
  • E5, C4, A3
  • E5, D3, C1
  • E1, D3, C5
  • E1, C2, A3

Keskustan läpi kulkee myös neljä tällaista ritarilinjaa:

  • A2, C3, E4
  • A4, C3, E2
  • B5, C3, D1
  • D5, C3, B1

Yhteenlaskettuna 12 ritarilinjaa saadaan 140 + 12 = 152.

Jos yhdistelmiä on yhteensä 2 300 ja lomakeviivoja 152, niin 2300 - 152 = 2 148 eivät muodosta viivoja ja muodostavat siten kolmioita.

Näin ollen vastauksemme on 2 148/2 300 = 93,39 %.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Sinulle annetaan:

  • Kahdeksan mailin matkan lentokone on suoraan ilmatorjuntaohjuksen yläpuolella, joka laukaistaan juuri sillä hetkellä.
  • Lentokone kulkee koko ajan suoraan suuntaan.
  • Lentokone kulkee 600 mailia tunnissa.
  • Ohjus kulkee 2000 mailia tunnissa.
  • Ohjus kulkee aina kulmassa, joka on suoraan lentokonetta kohti.

Kysymykset:

  • Kuinka pitkän matkan lentokone lentää ennen kuin ohjus osuu siihen?
  • Kuinka kauan ohjuksen osuminen lentokoneeseen kestää?
  • Kuinka pitkä on ohjuksen lentoreitti?

anonyymi

  • Kuinka pitkän matkan kone lentää ennen kuin ohjus osuu siihen? = 240/91 mailia
  • Kuinka kauan ohjuksen osuminen koneeseen kestää? = 2/455 tuntia
  • Kuinka kauan ohjus kulkee? = 800/91 mailia

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Olettaa:

  • 90 % yleisöstä käyttää maskeja.
  • Koronaviruksen saamisen todennäköisyys on maskia käyttävillä 1 % ja maskia käyttämättömillä 3 %.

Joku valitaan sattumanvaraisesti koronaviruksen kanssa. Mikä on todennäköisyys, että hän käyttää maskia?

anonyymi

Tämä on klassinen bayesilainen ehdollisen todennäköisyyden kysymys.

Vastaus on todennäköisyys (joku käyttää maskia ja hänellä on koronavirus) / todennäköisyys (jollakin on koronavirus) =

(0,9 * 0,01) / (0,9 * 0,01 + 0,1 * 0,03) = 75 %.

Neliön keskellä on muurahainen. Se on 17 tuuman päässä vasemmasta yläkulmasta, 20 tuuman päässä oikeasta yläkulmasta ja 13 tuuman päässä oikeasta alakulmasta.

Kuinka suuri neliö on?

anonyymi

c^2 = a^2 + b^2 -2ab*cos(c)
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)

369 neliötuumaa.

Kierrä ensin kolmiota ABE 90 astetta muodostaaksesi uuden kolmion BDF.

Koska kolmiota on kierretty 90 astetta, kulma EBF = 90, määritelmän mukaan. Pythagoraan kaavan mukaan EF = 20*sqrt(2).

Kosinien lain mukaan: 17^2 = 13^2 + (20*neliöjalka(2))^2 - 2*13*20*neliöjalka(2)*cos(DEF).

289 = 169 + 800 - 520 * neliöjuuri (2) * cos (DEF)

520 * neliöjuuri(2) * cos(DEF) = 680.

cos(DEF) = 17 * neliöjuuri(2) / 26.

Muista, sin^2(x) + cos^2(x) = 1. Käytetään sitä sin(DEF)-funktion ratkaisemiseen.

sin^2(DEF) + cos^2(DEF) = 1

sin^2(DEF) + (17*neliöyksikkö(2)/26)^2 = 1

sin^2(DEF) + 289/338 = 1

sin^2(DEF) = 49/338

sin(DEF) = 7 * neliöjuuri(2) / 26

Seuraavaksi tarkastellaan kulmaa BED.

Kulma BED = Kulma BEF + Kulma FED.

Tiedämme, että EBF on 90 astetta ja tasakylkinen kolmio. Se tekisi kulman BEF olevan 45 astetta.

Joten, kulma BED = 45 astetta + kulma FED.

Muista, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).

cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)

= (1/neliö(2))*17*neliö(2)/26 - (1/neliö(2))*7*neliö(2)/26

= (17/26) - (7/26) = 10/26 = 5/13

Sovelletaan kosinien lakia uudelleen, tällä kertaa kolmioon BED.

BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)

= 400 + 169 - 200 = 369

BD on kyseisen neliön sivu, joten BD^2 on kyseisen neliön pinta-ala, jonka olemme osoittaneet olevan 369.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Olet pyroteknikko, joka vastaa huvipuiston iltaisesta ilotulituksesta. Olet saanut Euroopasta uudenlaisia raketteja ja testaat yhtä niistä ajoittaaksesi sen näytöksesi musiikin tahtiin.

Ilotulitusraketti ammutaan pystysuunnassa ylöspäin tasaisella 4 ms^-2 kiihtyvyydellä, kunnes kemiallinen polttoaine loppuu. Sen nousu hidastuu sitten painovoiman vaikutuksesta, kunnes se saavuttaa maksimikorkeuden 138 metriä, jossa se räjähtää.

Olettaen, että ilmanvastusta ei ole ja painovoimakiihtyvyys on 9,8 metriä sekunnissa, kuinka kauan raketin kestää saavuttaa maksimikorkeutensa?

Gialmere

Vastaus on 483/49 = noin 9,8571 sekuntia.

Olkoon:
t = aika rakettipolttoaineen loppumisesta.
r = rakettipolttoaineen kestoaika

Aion ilmaista kiihtyvyyden ylöspäin suuntautuvana. Eli kiihtyvyys rakettipolttoaineiden palamisen jälkeen on -9,8.

Muistutuksena, kiihtyvyyden integraali on nopeus ja nopeuden integraali on sijainti. Määritetään sijainti suhteessa maahan.

Kun raketti laukaistaan ensimmäisen kerran, meille annetaan kiihtyvyydeksi 4.

Integraalin perusteella raketin nopeus r sekunnin kuluttua on 4r.

Nopeuden integraalin avulla saadaan raketin sijainti r sekunnin kuluttua, kun aika on 2r 2 .

Katsotaanpa nyt, mitä tapahtuu rakettipolttoaineen palamisen jälkeen.

Meille on annettu, että painovoiman kiihtyvyys on -9,8.

Painovoiman nopeus ajanhetkellä t on -9,8t. Sillä on kuitenkin myös raketista ylöspäin suuntautuva nopeus 4r.

Olkoon v(t) = nopeus ajanhetkellä t

v(t) = -9,8t + 4r

Raketti saavuttaa maksimikorkeuden, kun v(t) = 0. Ratkaistaanpa se.

v(t) = 0 = -9,8t + 4r
4r = 9,8t
t = 40/98 r = 20r/49.

Toisin sanoen, riippumatta siitä, kuinka kauan raketin polttoainetta riittää, raketti jatkaa matkaansa ylöspäin 20/49 tuosta ajasta.

Meille annetaan myös saavutetulla suurimmalla korkeudella kuljettu matka, joka on 138.

Otetaan v(t):n integraali saadaksemme kuljetun matkan kaavan, jota kutsumme d(t):ksi.

d(t) = -4,9t² + 4rt + c, missä c on integrointivakio.

Kuten jo osoitimme, raketti kulki matkan 2r2 polttoaineen loppuessa, joten sen täytyy olla integrointivakio. Tästä saadaan:

d(t) = -4,9t² + 4rt + 2r²

Tiedämme, että maksimikorkeus 138 saavutettiin ajanhetkellä 20r/49. Joten lisätään yhtälöön t=20r/49 ratkaistaksemme r:n:

d((20r/49) = -4,9((20r/49) 2 + 4r(20r/49) + 2r 2 = 138

r² *(-1960/2401 + 80/49 + 2) = 138

r2 = 49

r = 7

Joten rakettipolttoainetta riitti seitsemän sekuntia.

Tiedämme jo, että raketti jatkoi nousuaan 20/49 tuosta ajasta, mikä on 140/49 = noin 2,8571 sekuntia.

Näin ollen aika laukaisusta maksiminopeuteen on 7 + 140/49 = 483/49 = noin 9,8571 sekuntia

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kuinka monta kahden nopan heittoa tarvitaan, jotta saadaan jokainen yhteistulos 2:sta 12:een? Käytä ratkaisussasi differentiaali- ja integraalilaskentaa.

BruceZ

Noin 61.2173847639572 rullaa.

Muista, että todennäköisyys sille, että heitetään yhteensä 2, on 1/36. T:llä heitolla odotettu heittojen määrä, joiden kokonaismäärä on 2, on t/36. Oletetaan, että heittojen välinen aika on eksponentiaalisesti jakautunut keskiarvon ollessa t/36. Poissonin jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 2, on exp(-t/36).

Muista, että todennäköisyys sille, että heitetään yhteensä 3, on 2/36 = 1/18. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 3, on exp(-t/18).

Muista, että todennäköisyys sille, että heitetään yhteensä 4, on 3/36 = 1/12. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 4, on exp(-t/12).

Muista, että todennäköisyys sille, että heitetään yhteensä 5, on 4/36 = 1/9. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 5, on exp(-t/9).

Muista, että todennäköisyys sille, että heitetään lukuja yhteensä 6, on 5/36. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään lukuja yhteensä 6, on exp(-5t/36).

Muista, että todennäköisyys sille, että heitetään yhteensä 7, on 6/36 = 1/6. Samalla logiikalla Poisson-jakauma kertoo meille, että todennäköisyys sille, että heitetään yhteensä 7, on exp(-t/6).

Todennäköisyydet luvuille 8–12 ovat samat kuin luvuille 2–6.

Näin ollen todennäköisyys sille, että jokaisesta kokonaisluvusta t yksikköä on heitetty ainakin kerran, on:

(1-op(-t/36))^2 * (1-op(-t/18))^2 * (1-op(-t/12))^2 * (1-op(-t/9))^2 * (1-op(-5t/36))^2 * (1-op(-t/6))

Todennäköisyys, että ainakin kokonaissummaa EI ole laskettu t aikayksikössä, on 1 - (1-lauseke(-t/36))^2 * (1-lauseke(-t/18))^2 * (1-lauseke(-t/12))^2 * (1-lauseke(-t/9))^2 * (1-lauseke(-5t/36))^2 * (1-lauseke(-t/6))

Saadaksemme odotetun ajan ilman yhtäkään kokonaislukua, integroimme yllä olevan funktion nollasta äärettömyyteen.

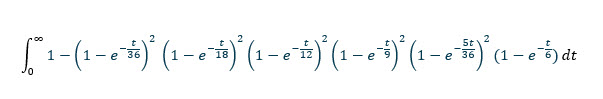
Integraalilaskuri (suosittelen tätä ) ratkaisee tämän helposti muodossa 769767316159/12574325400 = noin 61,2173847639572 rullaa.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Kuutio on kolmiulotteinen kappale, joka koostuu yksikköneliöistä.

kuutiomainen

Särmiö a × b × c muodostetaan abc identtisestä yksikkökuutiosta, kuten 3x3x3 Rubikin kuutio. Jaa kuutiot kahteen toisensa poissulkevaan tyyppiin. Ulkoiset kuutiot muodostavat särmiön sivut; sisäkuutiot ovat täysin suljettuja. Esimerkiksi kuvassa olevassa särmiössä on 74 ulkoista ja 10 sisäistä kuutiota.

Anna kaikkien sellaisten suorakulmaisten särmiöiden mitat, joilla on ulkoisten kuutioiden lukumäärä yhtä suuri kuin sisäisten kuutioiden lukumäärä.

Gialmere

Tällaisia särmiöitä on 20 mahdollista.
  1. 5 × 13 × 132
  2. 5 x 14 x 72
  3. 5 x 15 x 52
  4. 5 x 16 x 42
  5. 5 x 17 x 36
  6. 5 x 18 x 32
  7. 5 x 20 x 27
  8. 5 x 22 x 24
  9. 6 x 9 x 56
  10. 6 x 10 x 32
  11. 6 x 11 x 24
  12. 6 x 12 x 20
  13. 6 x 14 x 16
  14. 7 x 7 x 100
  15. 7 x 8 x 30
  16. 7 x 9 x 20
  17. 7 x 10 x 16
  18. 8 x 8 x 18
  19. 8 x 9 x 14
  20. 8 x 10 x 12

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Olkoon 0 < a < b. Kumpi on enemmän a^b vai b^a?

anonyymi

Vastaus riippuu erityisesti kohdista a ja b, mutta kaksi nyrkkisääntöä sopivat useimpiin tilanteisiin.

Jos a > e, niin a^b > b^a

Jos b < e, niin a^b < b^a

Jos a < e ja b > e, niin tietoa ei ole riittävästi määrittämiseen.

Tässä on ratkaisu (PDF).

Kranaatti heitetään pohjattomaan kuiluun. Keskimäärin kranaatti räjähtää kuudessa sekunnissa. Aika räjähdykseen on muistiton ominaisuus, eli räjähdyksen todennäköisyys millä tahansa hetkellä on aina sama ja riippumaton siitä, kuinka kauan on kulunut siitä, kun neula vedettiin irti. Toisin sanoen sen elinikä noudattaa eksponentiaalista jakaumaa. Oletetaan kiihtyvyys 32 jalkaa sekunnissa.

Ace2

1 152 jalkaa

Tässä on koko ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kuvitellaanpa peliohjelma, jossa kaksi kilpailijaa ovat sekä itsekkäitä että täydellisiä loogikoita. Tässä ovat säännöt.

  1. Juontaja asettaa miljoona dollaria pöydälle kahden kilpailijan väliin.
  2. Kilpailijaa A pyydetään tekemään ehdotus siitä, miten rahat jaetaan kahden kilpailijan kesken.
  3. Kilpailijaa B pyydetään hyväksymään tai hylkäämään ehdotus.
  4. Jos kilpailija B hyväksyy ehdotuksen, he jakavat rahat sillä tavalla ja peli on ohi.
  5. Jos kilpailija B hylkää ehdotuksen, juontaja poistaa 10 % pöydällä olevasta summasta.
  6. Juontaja pyytää sitten kilpailijaa B tekemään ehdotuksen, ja kilpailijalla A on sama mahdollisuus hyväksyä tai hylätä se.
  7. Jos kilpailija A hyväksyy ehdotuksen, se jaetaan ja peli on ohi. Jos hän hylkää ehdotuksen, juontaja tekee pöydälle vielä 10 % jäljellä olevasta summasta. Sitten palataan vaiheeseen 2 ja toistetaan, kunnes ehdotus hyväksytään.

Kysymys kuuluu, miten kilpailijan A tulisi ehdottaa rahojen jakamista ensimmäisellä vuorollaan?

anonyymi

Hänen tulisi ehdottaa, että hän pitää 10/19 rahoista itsellään, vähennettynä yhdellä pennin, ja tarjota hänelle 8 9/19 rahoista sekä yhden pennin. Toisin sanoen:

V: 526 315,78 dollaria
B: 473 684,22 dollaria

Avainasemassa on, että A:n tulisi asettaa B mahdollisimman lähelle indifferenssipistettä.

Kutsutaan potin ja toisen pelaajan potin suhdetta r:ksi. Jos B hyväksyy tarjouksen, hän saa r × 1 000 000 dollaria.

Jos B hylkää tarjouksen, juontaja saa 10 % osuudesta, minkä jälkeen B:llä on asemaetu ja hän tarjoaisi kilpailijalle A osuuden r:stä ja pitäisi 1 r:n itsellään.

Ratkaisemassa r...

r × 1 000 000 $ = (1 - r) × 900 000 $.
r × 1 900 000 dollaria = 900 000 dollaria.
r = 900 000 dollaria / 1 900 000 dollaria = 9/19.

A ei halua B:n olevan täysin välinpitämätön, ettei a valitsisi sattumanvaraisesti ja isännällä olisi mahdollisuus kaataa potti. Joten A:n pitäisi heittää ylimääräinen pennin B:lle ja tarjota hänelle (9/19) × 1 000 000 dollaria + 0,01 dollaria = 473 684,22 dollaria.

V: 526 315,78 dollaria
B: 473 684,22 dollaria

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kaksi kaupunkia, Fauntleroy ja Southworth, sijaitsevat suoraan kanavan toisella puolella. Kaksi lauttaa kulkee edestakaisin koko päivän näiden kahden kaupungin välillä. Lautat kulkevat eri nopeuksilla. Samaan aikaan ne molemmat lähtevät liikkeelle, yksi kummastakin kaupungista.

Ensimmäisellä kerralla ne ylittävät tien 8 kilometrin päässä Southworthista. Toisella kerralla ne ylittävät tien 5 kilometrin päässä Fauntleroysta. Oleta, ettei lastaukseen ja purkuun ole aikaa, mutta molemmat tekevät välittömästi U-käännöksen. Oleta myös, että ne kulkevat suoraan.

Kuinka kaukana nuo kaksi kaupunkia ovat toisistaan?

anonyymi

12 mailia

Olkoon t 1 = aika ensimmäiseen ylitykseen
Olkoon t2 = aika toiseen ylitykseen
r = Fauntleroysta lähtevän lautan nopeuden suhde Southworthista lähtevän lautan nopeuteen.
c = Kanavan etäisyys kahden kaupungin välillä.

Meille annetaan, että heidän ensimmäinen ylityksensä on 5 mailin päässä Southworthista. Ilmaistaan tämä kaavoilla:

c-5 = r* t1
5 = t1

Yhtälöimällä t1 saadaan:

c-5 = 5r tai r = (c-5)/5

Meille annetaan myös, että toinen ylityskerta on 3 mailin päässä Fauntleroysta. Ilmaistaan tämä kaavoilla:

3c - 3 = r* t2
c+3 = t²

Yhtälöimällä t2 saadaan:

2c - 3 = r*(c+3)

Korvaa r=(c-5)/5

2c-3 = [(c-5)/5] * (c+3)
10c - 15 = c^2 - 2c - 15
c^2 - 12c = 0 c - 12 = 0 c = 12

Joten kanava on 12 mailia pitkä.

Mikä on sinisen alueen pinta-ala seuraavassa kaaviossa?

anonyymi

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

1/2

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Shakkiturnauksessa jokainen kilpailija pelaa ottelun jokaista toista kilpailijaa vastaan. Jokainen kilpailija saa 1 pisteen jokaisesta voittamastaan ottelusta, 0,5 pistettä jokaisesta tasapelistä ja 0 pistettä jokaisesta hävitystä pelistä.

Turnauksen lopussa nähdään, että kaikki kilpailijat saivat eri määrän pisteitä ja pistetilanteen viimeinen kilpailija voitti kaikki kolme parasta kilpailijaa.

Mikä on siis turnaukseen osallistuvien kilpailijoiden vähimmäismäärä?

Gialmere

13

Kutsutaan pelaajien lukumäärää n:ksi.

Arvioisin, että viimeiseksi sijoittuneella pelaajalla on vain kolme voittoa, kolmea parasta vastaan, ja hän on hävinnyt joka toisen pelin. Se antaa hänelle kolme pistettä.

Sitten lasken jokaisen seuraavan pelaajan pistejärjestyksessä olevan 0,5 pistettä enemmän kuin edellinen rankingissa. Tämä antaisi korkeimmalle rankatulle pelaajalle 3+(n-1)/2 pistettä.

Laskemalla luvun 3 summaksi 3 + (n - 1) / 2, lisäämällä 1/2 pistettä askelta kohden, saadaan (((n + 5) * (n + 6) / 2) - 15) / 2.

n pelaajan yhteispistemäärä on n*(n-1)/2, jossa kaikki pelaavat kaikkia toisiaan vastaan kerran. Jokaisesta pelistä saa yhden pisteen, ja se on myös kaikkien pelaajien kesken ansaittujen pisteiden kokonaismäärä.

Ratkaise sitten n:n arvo:

(((n+5)*(n+6)/2)-15)/2 = n*(n-1)/2
((n+5)*(n+6)/2)-15 = n*(n-1)
(n+5)*(n+6)/2 = n*(n-1) + 15
(n+5)*(n+6) = 2*n*(n-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
n^2 + 11n = 2n^2 - 2n
n + 11 = 2n⁻²
n=13

Seuraava taulukko näyttää, miten tämä voi tapahtua. Taulukon runko näyttää voittajan kaikissa 78 pelissä.

Seuraava taulukko näyttää kunkin pelaajan pistemäärän.

Pelaajan kokonaispisteet

Pelaaja Pisteet
13 3
12 3.5
11 4
10 4.5
9 5
8 5.5
7 6
6 6.5
5 7
4 7.5
3 8
2 8.5
1 9

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kumpi on tehokkaampi tapa pinota tykinkuulia, neliönmuotoiseen pyramidiin, kuten Egyptin pyramideissa, vai kolmionmuotoiseen tetraedriin?

anonyymi

Tässä on pari kaavaa, joista lukija voi olla hyödyllinen:

1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6

1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6

Vieritä alaspäin nähdäksesi vastaukseni ja ratkaisuni.

Oletan "tehokkaalla" tarkoittavan sitä, missä tykinkuulien välissä on vähiten hukkaan heitettyä tilaa.

Yksinkertaisuuden vuoksi kummankin pyramidin tilavuuden määrittämiseksi käytetään pyramidin kulmissa sijaitsevien kuulien keskipistettä. Olkoon n tykinkuulien lukumäärä kummankin pyramidin pohjan sivulla.

Tarkastellaan ensin neliöpohjaista pyramidia.

Koko pyramidissa on tykinkuulia, joiden lukumäärä on 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 + ... + n 2 = n*(n+1)*(2n+1)/6.

Seuraavaksi etsitään tämän neliöpyramidin korkeus, jonka pohjan sivu on n. Kuten kuvasta näkyy, sivut (muut kuin neliöpohja) ovat tasasivuisia kolmioita. Näin ollen vino korkeus on myös n. Etäisyys pohjan yhdestä kulmasta vastakkaiseen kulmaan on n*sqrt(2). Etäisyys pohjan kulmasta pohjan keskipisteeseen on siis n*sqrt(2)/2. Olkoon korkeus h. Tarkastellaan suorakulmaista kolmiota, jonka muodostavat korkeus, etäisyys pohjan kulmasta pohjan keskipisteeseen ja vino korkeus.

h² + (n*neliöluku(2)/2) ² = n²
h = n*neliöluku(2)/2.

Muista, että pyramidin tilavuus on pohja * korkeus / 3. Tämä tekee pyramidin tilavuuden:

n 2 * n* sqrt(2)/2 * (1/3) = n 3 *sqrt(2)/6.

Pallojen suhde tilavuuteen on siis [n*(n+1)*(2n+1)/6] / [ n³ *sqrt(2)/6] = sqrt(2)*n*(n+1)*(2n+1)/(2* n³ ) = sqrt(2)*(n+1)*(2n+1)/(2* n² )

Seuraavaksi tarkastellaan pyramidia, jolla on kolmionmuotoinen pohja.

Koko pyramidissa on tykinkuulia 1 + 3 + 6 + 10 + 15 + ... + n*(n+1)/2 = n*(n+1)*(n+2)/6.

Seuraavaksi lasketaan pohjan pinta-ala. Muista, että kolmion, jonka sivut ovat 30-60-90, sivut ovat verrannollisia lukuun 1/2, neliö(3)/2 ja 1. Tästä ei ole vaikeaa löytää sivun n omaavan tasasivuisen kolmion korkeutta, joka on n*neliö(3)/2. Tämä tekee pohjan n pinta-alaksi 2 *neliö(3)/4.

Etäisyys pohjan kulmasta pohjan keskipisteeseen on neliö(3)/3. Koska tämä ja pyramidin vino korkeus on 1, voimme käyttää Pythagoraan lauseketta pyramidin korkeuden laskemiseen neliö(6)/3:na.

Voimme nyt laskea pyramidin tilavuuden kaavalla pohja * korkeus / 3 = ( n² * neliöjuuri(3) / 4) * (n* neliöjuuri(6) / 3) * (1/3) = n³ * neliöjuuri(18) / 36 = n³ * neliöjuuri(2) / 12.

Pallojen suhde tilavuuteen on siis [n*(n+1)*(n+2)/6] / [ n³ *sqrt(2)/12] = sqrt(2)*n*(n+1)*(2n+1)/(2* n³ ) = sqrt(2)*(n+1)*(n+2)/ n²

Tässä on vertailu pallojen ja tilavuuden suhteista:

  • Neliöpohja: sqrt(2)*(n+1)*(2n+1)/(2* n² )
  • Kolmion kanta: sqrt(2)*(n+1)*(n+2)/ n²

Jaetaan molemmat suhteet luvulla sqrt(2)*(n+1)/ n² :

  • Neliöpohja: (2n+1)/2 = n + 0,5
  • Kolmion kanta: n+2

Kun n kasvaa, kuulien ja tilavuuden suhde lähestyy arvoa n molemmissa pyramideissa. Toisin sanoen, mitä suurempi määrä tykinkuulia on, sitä tehokkaampia ne ovat.

Kun otetaan huomioon tykinkuulan tilavuus, molempien pyramidien hyötysuhde, joka määritellään tykinkuulan tilavuuden ja kokonaistilavuuden suhteena, lähestyy arvoa pi*sqrt(2)/6 = ~ noin 74,05 %.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Mikä on minkä tahansa suuren luvun lähellä olevien alkulukujen keskimääräinen etäisyys? Kuinka monta alkulukua on tätä lukua pienempiä?

anonyymi

Erittäin hyvä arvio alkulukujen välisen keskimääräisen etäisyyden kuvaamiseksi lähellä mitä tahansa suurta lukua n on ln(n). On huomionarvoista, kuinka hyvä tämä estimaattori on.

Todisteena seuraava taulukko esittää ensimmäisten 15 miljoonan alkuluvun vaihteluvälin miljoonan kappaleen ryhmissä. Taulukko näyttää alkulukujen välisen keskimääräisen etäisyyden vaihteluvälillä ja keskimääräisen etäisyyden arvion. Arvio on vaihteluvälin suurimman ja pienimmän alkuluvun keskiarvon luonnollinen logaritmi. Esimerkiksi miljoonan alkuluvun 15. ryhmälle se on ln((256 203 221 + 275 604 541) / 2).

Alkulukujen keskimääräinen etäisyys

Ensimmäinen pääministeri
alueella		 Viimeinen alku
alueella		 Alkulukuja
alueella		 Keskimääräinen etäisyys Arvio
2 15 485 863 1 000 000 15.485861 15.86229105
15 485 867 32 452 843 1 000 000 16.966976 16.9922867
32 452 867 49 979 687 1 000 000 17.52682 17.53434381
49 979 693 67 867 967 1 000 000 17.888274 17.89175615
67 867 979 86 028 121 1 000 000 18.160142 18.15864108
86 028 157 104 395 301 1 000 000 18.367144 18.3716137
104 395 303 122 949 823 1 000 000 18.55452 18.54883262
122 949 829 141 650 939 1 000 000 18.70111 18.70058553
141 650 963 160 481 183 1 000 000 18.83022 18.83322787
160 481 219 179 424 673 1 000 000 18.943454 18.95103217
179 424 691 198 491 317 1 000 000 19.066626 19.05703535
198 491 329 217 645 177 1 000 000 19.153848 19.15337672
217 645 199 236 887 691 1 000 000 19.242492 19.24163365
236 887 699 256 203 161 1 000 000 19.315462 19.32305683
256 203 221 275 604 541 1 000 000 19.40132 19.39864545

Lähde: Primeiden väliset aukot Prime Pagesissa.

Saadaksemme minkä tahansa luvun alle olevien alkulukujen lukumäärän, voimme aloittaa integroimalla ln(n):n keskimääräisen etäisyyden estimaatin. Tämä antaa meille alkulukujen välisten keskimääräisten etäisyyksien summan mihin tahansa lukuun n asti.

Mikä on funktion f(n)=ln(n) integraali? Muista, että osittaisella integroinnilla saadaan seuraava kuvaus:

Funktion f(n)*g'(n) integraali dn = f(n)*g(n) - funktion (f'(n)*g(n)) integraali dn

Olkoon f(n)=ln(n) ja g'(n)=1. Tällöin f'(n)=1/n ja g(n)=n. ln(n):n integraali on siis ln(n)*n - ((1/n)*n):n integraali = ln(n)*n - n = n*(ln(n)-1)

Jos jaamme n*(ln(n)-1) luvulla n, saamme alkulukujen keskimääräisen etäisyyden lukuvälillä 2-n. Tämä on ln(n)-1.

Jos jaamme n tällä alkulukujen keskimääräisellä etäisyydellä, saamme alkulukujen keskimääräisen lukumäärän, jonka etäisyydellä n on n, eli n/(ln(n)-1).

Todisteena seuraava taulukko näyttää alkulukujen lukumäärän eri suurilla luvuilla ja niiden arvioidun arvon. Pahoittelen 15 merkitsevän numeron tarkkuutta, joka on kaikki mitä Excel sallii. Joku voisi tehdä laskentataulukon, joka pystyy käsittelemään enemmän.

Alkulukujen keskimääräinen etäisyys

n Alkulukujen n alainen n/(ln(n)-1)
10 4 8
100 25 28
1 000 168 169
10 000 1 229 1 218
100 000 9 592 9 512
1 000 000 78 498 78 030
10 000 000 664 579 661 459
100 000 000 5 761 455 5 740 304
1 000 000 000 50 847 534 50 701 542
10 000 000 000 455 052 511 454 011 971
100 000 000 000 4 118 054 813 4 110 416 301
1 000 000 000 000 37 607 912 018 37 550 193 650
10 000 000 000 000 346 065 536 839 345 618 860 221
100 000 000 000 000 3 204 941 750 802 3 201 414 635 781
1 000 000 000 000 000 29 844 570 422 669 29 816 233 849 001
10 000 000 000 000 000 279 238 341 033 925 279 007 258 230 820
100 000 000 000 000 000 000 2 623 557 157 654 230 2 621 647 966 812 030
1 000 000 000 000 000 000 24 739 954 287 740 800 24 723 998 785 920 000
10 000 000 000 000 000 000 000 234 057 667 276 344 000 233 922 961 602 470 000
100 000 000 000 000 000 000 000 2 220 819 602 560 910 000 2 219 671 974 013 730 000
1 000 000 000 000 000 000 000 21 127 269 486 018 700 000 21 117 412 262 910 000 000
10 000 000 000 000 000 000 000 000 201 467 286 689 315 000 000 201 381 995 844 660 000 000
100 000 000 000 000 000 000 000 000 1 925 320 391 606 800 000 000 1 924 577 459 166 810 000 000
1 000 000 000 000 000 000 000 000 000 18 435 599 767 349 200 000 000 18 429 088 896 563 900 000 000
10 000 000 000 000 000 000 000 000 000 176 846 309 399 143 000 000 000 176 788 931 049 964 000 000 000

Lähde: Kuinka monta Primet ovat olemassa? osoitteessa Prime Pages.

nonagon

Yllä oleva kuva on yhdeksänkulmio, jonka sivun pituus on yksi.

Kumpi on enemmän, AB+AC vai AE?

Tämä ongelma on otettu Mensa Bulletinin maaliskuun 2021 numerosta.

anonyymi

Nämä kaksi ovat yhtä suuret.

Tässä on ratkaisuni tähän ongelmaan. (PDF)

Miten voin helposti löytää minkä tahansa kolmi- tai nelinumeroisen luvun neliöjuuren olettaen, että vastaus on kokonaisluku?

anonyymi

Seuraavassa taulukossa näkyvät numerot 0–9, kunkin neliön ja kyseisen neliön viimeisen numeron.

Neliölukujen viimeinen numero

Alkuperäinen
Määrä		 Neliö Viimeinen numero
neliöstä
0 0 0
1 1 1
2 4 4
3 9 9
4 16 6
5 25 5
6 36 6
7 49 9
8 64 4
9 81 1

Huomaa, että parilliset neliöluvut päättyvät aina lukuun 0, 1, 4, 5, 6 tai 9. Tämä pätee kaikkiin neliöihin. Tämä johtuu siitä, että alkuperäisen luvun viimeinen numero määrää neliön viimeisen numeron.

Vaihe 1: Neliön viimeisen numeron perusteella voimme käyttää seuraavaa taulukkoa neliöjuuren viimeisen numeron rajaamiseen. Esimerkiksi jos 2809 on neliö, niin neliöjuuren viimeinen numero on 3 tai 7.

Alkuperäisen numeron viimeinen numero

Viimeinen numero
neliöjuuresta		 Viimeinen numero
neliöstä
0 0
1 1 tai 9
4 2 tai 8
5 5
6 4 tai 6
9 3 tai 7

Vaihe 2: Seuraavaksi ota alkuperäinen luku ja poista siitä kaksi oikeanpuoleista numeroa. Esimerkiksi, jos alkuperäinen luku oli 2809, käytä lukua 28.

Vaihe 3: Etsi pienin neliöluku, joka on pienempi tai yhtä suuri kuin vaiheen 2 tulos. Ota sitten kyseisen neliöluvun neliöjuuri. Esimerkiksi pienin neliö, joka on pienempi kuin 28, on 25. Ota luvun 25 neliöjuuri, niin saat 5.

Jos et ole muistanut neliöitä sataan asti, voit käyttää seuraavaa taulukkoa.

Neliöjuuren ensimmäinen osa

Vaihe 2 Vaihe 3
1–3 1
4–8 2
9–15 3
16–24 4
25–35 5
36–48 6
49–63 7
64–80 8
81–99 9

Vaihe 4: Jos vaiheen 1 tulos on 0 tai 5, lisää se vaiheen 3 tuloksen jälkeen ja olet valmis.

Muussa tapauksessa olkoon a = vaiheen 3 tulos. Olkoon b = a×(a+1). Esimerkiksi, jos vaiheen 3 tulos on 5, niin b = 5×6 = 30.

Vaihe 5: Jos b < a, neliöjuuren viimeinen numero on vaiheen 1 mahdollisuuksista pienempi. Muussa tapauksessa, jos b > = a, se on kahdesta mahdollisuudesta suurempi.

Vaihe 6: Saat neliöjuuren ottamalla vaiheen 3 tuloksen ja sen jälkeen vaiheen 5 tuloksen. Toisin sanoen 10 × (vaihe 3) + vaihe 5.

Katsotaanpa joitakin esimerkkejä:

Etsi luvun 256 neliöjuuri.

  • Vaihe 1: Neliöjuuren viimeinen numero on 4 tai 6.
  • Vaihe 2: Pudottamalla kaksi viimeistä numeroa saadaan 2.
  • Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 2, on 1. Luvun 1 neliöjuuri on 1.
  • Vaihe 4: 1 * (1 + 1) = 2.
  • Vaihe 5: Vaiheen 4 tulos on yhtä suuri kuin vaiheen 2 tulos, joten käytämme viimeisenä numerona vaiheen 1 vaihtoehdoista suurempaa, joka on 6.
  • Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 1 ja 6 = 16.

Etsi luvun 1369 neliöjuuri.

  • Vaihe 1: Neliöjuuren viimeinen numero on 3 tai 7.
  • Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 13.
  • Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 13, on 9. Luvun 9 neliöjuuri on 3.
  • Vaihe 4: 3 * (1 + 3) = 12.
  • Vaihe 5: Vaiheen 2 tulos on suurempi kuin vaiheen 4 tulos, joten käytämme viimeisenä numerona vaiheen 1 vaihtoehdoista suurempaa, joka on 7.
  • Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 3 ja 7 = 37.

Laske luvun 2704 neliöjuuri.

  • Vaihe 1: Neliöjuuren viimeinen numero on 2 tai 8.
  • Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 27.
  • Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 27, on 25. Luvun 25 neliöjuuri on 5.
  • Vaihe 4: 5 * (1 + 5) = 60.
  • Vaihe 5: Vaiheen 2 tulos on pienempi kuin vaiheen 4 tulos, joten käytämme vaiheen 1 vaihtoehdoista pienempää viimeisenä numerona, joka on 2.
  • Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 5 ja 2 = 52.

Laske luvun 5625 neliöjuuri.

  • Vaihe 1: Neliöjuuren viimeinen numero on 5.
  • Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 56.
  • Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 56, on 49. Luvun 49 neliöjuuri on 7.
  • Vaihe 4: Vaiheen 1 tulos on 0 tai 5, joten vastaus on vaiheen 3 tulos lisättynä vaiheen 1 tuloksella: 7 ja 5 = 75

Laske luvun 6561 neliöjuuri.

  • Vaihe 1: Viimeinen numero on 1 tai 9.
  • Vaihe 2: Jättämällä pois kaksi viimeistä numeroa saamme luvun 65.
  • Vaihe 3: Pienin neliö, joka on pienempi tai yhtä suuri kuin 65, on 64. Luvun 64 neliöjuuri on 8.
  • Vaihe 4: 8 * (1 + 8) = 72.
  • Vaihe 5: Vaiheen 2 tulos on pienempi kuin vaiheen 4 tulos, joten käytämme vaiheen 1 vaihtoehdoista pienempää viimeisenä numerona, joka on 1.
  • Vaihe 6: Neliöjuuri on luvun 3 tulos, johon on liitetty vaiheen 5 tulos, jolloin saadaan 8 ja 1 = 81.

Voit katsoa tämän menetelmän esittelyn YouTubesta .

Mikä on säännöllisen viisikulmion pinta-ala, kun sen sivun pituus on 1?

anonyymi

Napsauta alla olevaa ruutua nähdäksesi vastauksen.

(neliöluku(5)/4)*neliöluku(5+2*neliöluku(5)) = noin 1,72047740058897.

Napsauta alla olevaa ruutua saadaksesi vihjeen.

Pentagonin vihje

Tarkastellaan yllä olevaa kuvaa. AC = CD.

Tässä on ratkaisuni (PDF)

Tuulettomana päivänä Charlie ottaa kanoottinsa joelle ja meloo ylävirtaan. Hän meloo aina samaa vauhtia (toisin sanoen, jos jätämme virran huomiotta, hän meloisi aina samaa vauhtia). Mailin kuluttua vesillelaskusta hänen hatunsa putoaa jokeen. Kymmenen minuuttia myöhemmin hän huomaa hatunsa kadonneen ja tekee välittömästi U-käännöksen tavoittaakseen sen alavirtaan. Charlie saavuttaa hatunsa samasta paikasta, josta hän laski veden.

Kuinka nopea virta on?

anonyymi

Klikkaa alla olevaa painiketta nähdäksesi vastauksen.

3 mailia tunnissa.

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Seuraava kysymys liittyy setelin panokseen. Käytetään satunnaista yhdysvaltalaista sarjanumeroa mille tahansa setelille. Pelaaja valitsee kolme numeroa väliltä 0-9. Hänen on valittava kolme eri numeroa. Voitot perustuvat siihen, kuinka monta näistä kolmesta valitusta numerosta esiintyy sarjanumerossa vähintään kerran.

Jos pelaaja esimerkiksi valitsee 7-0-2 ja sarjanumero on 22227755, niin silloin on kaksi osumaa. Sillä ei ole merkitystä, että 2 ja 7 osuivat oikein useita kertoja.

Tässä ovat tarjotut kertoimet:

  • 3 ottelua: 5-1
  • 2 ottelua: 1–1
  • 1 ottelu: 9–5
  • 0 ottelua: 15-1

Mikä on kunkin vedon voittotodennäköisyys ja talon etu?

anonyymi

Seuraava taulukko näyttää voittoyhdistelmien määrän, voittotodennäköisyyden ja talon edun kullekin panokselle. Oikea sarake näyttää talon edun vaihtelevan 7,4 %:n ja 8,5 %:n välillä.

Sarjanumerovedot

Ottelut Maksaa Yhdistelmät Todennäköisyys Talon etu
3 5 15 426 684 0,154267 0,074399
2 1 45 771 270 0,457713 0,084575
1 1.8 33 037 245 0,330372 0,074957
0 15 5 764 801 0,057648 0,077632

Muodosta kolme murtolukua, joissa kussakin on yksi numero osoittajassa ja kaksi numeroa nimittäjässä ja joiden summa on yksi. Käytä jokaista numeroa 1–9 täsmälleen kerran.

Esimerkiksi 8/16 + 9/27 + 3/24 täyttää kaikki ehdot, paitsi että summa on 23/24, ei 1.

Gialmere

5/34 + 7/68 + 9/12

Vastauksen löytämiseksi on läpikäytävänä 60 480 mahdollista permutaatiota, kuten permut(9,3)*permut(6,3)*permut(3,3)/fact(3). Minun on myönnettävä, että yritin ainakin tunnin yrityksen ja erehdyksen kautta löytämättä ratkaisua.

Kirjoitin siis ohjelman, joka lajittelee läpi kaikki fact(9) = 362 880 tapaa lajitella yhdeksän numeroa ja testasin niitä kaikkia. Hankala osuus oli lajitella läpi kaikki mahdolliset tavat järjestää yhdeksän numeroa. Näin se tehdään leksografista lajittelua käyttäen.

  1. Laita kaikki yhdeksän alkiota taulukkoon järjestettynä pienimmästä suurimpaan.
  2. Etsi taulukon viimeinen alkio siten, että seuraava alkio on suurempi. Jos yhtäkään alkiota ei löydy, lopeta ohjelma.
  3. Aloittamalla vaiheen 2 jälkeisestä alkiosta etsi taulukon viimeinen alkio, joka on suurempi kuin vaiheen 2 alkio.
  4. Vaihda vaiheiden 2 ja 3 taulukon elementit keskenään.
  5. Käännä taulukon alkiot päinvastaisiksi vaiheen 2 jälkeisestä alkiosta loppuun asti.
  6. Palaa vaiheeseen 2

Tämän prosessin jälkeen löydät oikean vastauksen kuusi kertaa, kerran kaikille kuudelle tavalle järjestää kolme murtolukua.

Kirjoitin seuraavan koodin lajittelemaan jokaisen numeron 1:stä 9:ään leksografiseen järjestykseen ja testaamaan jokaisen, oliko se ratkaisu.


void kolme_murtoluku(tyhjä)
{
 int i, x_max, y_max, temp_array[100], hold, pt;
 int lex_array[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
 int elementtien_määrä = koko(lex_array) / koko(lex_array[0]);
 kokonaislukumäärä = 0;
 totuusarvo stop = false;
 kaksinkertainen yhteensä3;
 cerr << "Elementtien lukumäärä =\t" << elementtien_lukumäärä << "\n";
 tehdä
 {
  määrä++;
  tot3 = (double)lex_array[0] / (double)(10 * lex_array[1] + lex_array[2]);
  tot3 += (double)lex_array[3] / (double)(10 * lex_array[4] + lex_array[5]);
  tot3 += (double)lex_array[6] / (double)(10 * lex_array[7] + lex_array[8]); 
  jos (yhteensä3 == 1.0)
  {
   cerr << count << "\t";
   cerr << lex_array[0] << "/" << lex_array[1] << lex_array[2] << " + ";
   cerr << lex_array[3] << "/" << lex_array[4] << lex_array[5] << " + ";
   cerr << lex_array[6] << "/" << lex_array[7] << lex_array[8] << "\n";
  } 
  x_maks = -1;
  for (i = 0; i < (elementtien_määrä - 1); i++)
  {
   jos (lex_array[i] < lex_array[i + 1])
    x_maks = i;
  }
  jos (x_max >= 0)
  {
   y_maks = 0;
   for (i = x_max + 1; i < elementtien_määrä; i++)
   {
    jos (lex_array[x_max] < lex_array[i])
     y_maks = i;
   }
   pidä = lex_array[x_max];
   lex_array[x_max] = lex_array[y_max];
   lex_array[y_max] = pidä;
   jos (x_max + 1 < elementtien_määrä - 1) // käännä
   {
    for (i = x_max + 1; i < elementtien_määrä; i++)
    {
     väliaikainen_taulukko[i] = lex_taulukko[i];
    }
    pt = 0;
    for (i = x_max + 1; i < elementtien_määrä; i++)
    {
     lex_array[i] = temp_array[elementtien_määrä - 1 - pt];
     pt++;
    }
   }
  }
  muu
   pysäkki = tosi;
 } while (stop == false);
}

Tätä kysymystä on kysytty ja siitä keskustellaan foorumillani Wizard of Vegasissa .

Miehellä oli kymmenen gallonan (10 gallonan) viinitynnyri ja kannu. Eräänä päivänä hän kaatoi kannun täyteen viiniä ja täytti sitten tynnyrin vedellä. Myöhemmin, kun viini ja vesi olivat sekoittuneet perusteellisesti, hän kaatoi toisen kannun täyteen ja täytti taas tynnyrin vedellä. Tynnyrissä oli sitten yhtä paljon viiniä ja vettä.

Mikä oli kannun tilavuus?

Gialmere

10-5*neliömetri(2) =~ 2,9289 gallonaa

Olkoon j = kannun tilavuus.

Ensimmäisen täytön jälkeen kannussa oli jäljellä 10 gallonaa viiniä. Kun viini oli korvattu vedellä, viinin suhde koko tynnyriin oli (10 gallonaa) / 10.

Kun kannu oli kauhonut laimennetun viinin, tynnyrissä oli jäljellä 10 gallonaa laimennettua viiniä. Puhtaan viinin määrä laimennetussa viinissä voidaan ilmaista seuraavasti:

(10 - j) * ((10 - j) / 10) = 5

(10 - j)^2 = 50

j^2 - 20j + 100 = 50

j^2 - 20j + 50 = 0

j = (20 +/- neliöjuuri(400-200))/2

j = (20 +/- 10*neliöyksikkö(2))/2

j = 10 +/- 5*neliömetriä(2)

Kannu ei voi olla tynnyriä suurempi, joten meidän on käytettävä negatiivista etumerkkiä:

j = 10 - 5*sqrt(2) = ~ noin 2,92893218813452 gallonaa.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Kiitospäivän kunniaksi sinä ja 19 matemaatikkoa istutte pyöreän pöydän ääreen. Kaikki pöydässä haluaisivat annoksen karpalokastiketta, joka sattuu olemaan juuri nyt edessäsi.

Ensin tarjoilet itsellesi. Sitten sen sijaan, että jakaisit kastiketta ympyrää, päätät antaa sen satunnaisesti joko vasemmalla tai oikealla puolellasi istuvalle henkilölle. He tekevät sitten samoin ja antavat sen satunnaisesti joko vasemmalla tai oikealla puolellaan istuvalle henkilölle. Tämä jatkuu, kunnes kaikki ovat jossain vaiheessa saaneet karpalokastikkeen.

Kenellä ympyrän 20 ihmisestä on suurimmat mahdollisuudet saada karpalokastike viimeisenä?

Gialmere

Kaikilla muilla on yhtäläiset mahdollisuudet saada karpalokastike viimeisenä.

Nimetään yksi matemaatikoista G. Jotta G olisi viimeinen, kahden asian on täytyttävä:

  1. Karpaloiden on ensin saavutettava jompikumpi G:n naapureista.
  2. Karpaloiden täytyy liikkua 19 asentoa vastakkaiseen suuntaan saavuttamatta koskaan G:tä.

Jotta karpalot olisivat viimeisiä, niiden on lopulta saavutettava jompikumpi naapureista. Todennäköisyys tälle on siis 100 %.

Sitten, mikä tahansa toisen osan todennäköisyys onkin, se on sama jokaiselle henkilölle. Näin ollen jokaisella henkilöllä on yhtä suuri todennäköisyys olla viimeinen.

Jos tuo selitys ei ollut selvä. Gialmere sai tämän tehtävän fivethirtyeight.com-sivustolta. Tässä he selittävät ratkaisun . Vieritä alas kohtaan, jossa lukee "Ratkaisu viime viikon Arvuuttajaklassikkoon".

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Tässä on toinen pulmapeli Arvuuttajalta .

Pussissa on 100 marmorikuulaa. Jokainen marmorikuula on joko punainen, sininen tai vihreä. Jos pussista nostettaisiin kolme marmorikuulaa, todennäköisyys saada yksi kutakin väriä olisi 20 %. Kuinka monta marmorikuulaa pussissa on kutakin väriä? Huomaa, etten nimenomaisesti maininnut, nostetaanko marmorit takaisin paikoilleen vai ei.

Gialmere

Punaisten, sinisten ja vihreiden marmorikuulien määrä on 21, 35 ja 44, missä tahansa järjestyksessä. Ne nostetaan pussista ilman takaisinottoa.

Yritetään ratkaista se "palautusoletuksella". Olkoot r, b ja g punaisten, sinisten ja vihreiden marmorien lukumäärät. Tällöin todennäköisyys saada yksi kuula kutakin väriä olisi 6*(r/100)*(b/100)*(g/100). Asettamalla sen arvoksi 0,2 voimme sanoa:

6*(r/100)*(b/100)*(g/100) = 0,2
6*r*b*g = 200000

Luku 6 ei jakaudu tasan 200 000:een. Näin ollen luvulle r*b*g = 33333,333 ei ole kokonaislukuratkaisuja... Voimme siis sulkea pois sijoituksen avulla piirtämisen.

Kokeillaan seuraavaksi oletusta "ilman palautusta". Tässä tapauksessa todennäköisyys sille, että jokainen väri piirretään, on r*b*g/combin(100,3) = 0,2. Yritetään ratkaista se...

r*b*g/161700 = 0,2
r*b*g = 32340

Luvun 32340 alkutekijöihinjako on 2*2*3*5*7*7*11.

Meidän on jaettava nämä tekijät r:n, b:n ja g:n kesken pitäen samalla r+b+g=100. Voisimme esimerkiksi kokeilla:

r = 2 * 3 * 5 = 30
b = 2 * 11 = 22
g = 7 * 7 = 49

Vaikka nämä käyttävät oikein kaikki alkuluvut, r+b+g = 101, joten se ei ole pätevä ratkaisu.

Pelkäänpä, että minun piti kirjoittaa raa'alla voimalla toimiva silmukkaohjelma saadakseni ratkaisun r:n, b:n ja g:n arvoille 21, 35 ja 44 missä tahansa järjestyksessä.

Seuraava kysymys tulee meille Riddler Expressin tarjoamana.

Oletetaan NFL:n säännöt. Tarkastellaan seuraavaa tilannetta:

  • Punainen joukkue on 14 pistettä tappiolla pelin loppupuolella.
  • Punaisella joukkueella on kaksi hyökkäystä lisää
  • Sinisellä joukkueella ei ole enää yhtään hyökkäystä
  • Jätetään kenttämaalit ja safety-maalit huomiotta, sillä punaisen joukkueen on tehtävä kaksi touchdownia voidakseen voittaa.
  • Jos peli menee jatkoajalle, kummallakin joukkueella on 50 %:n mahdollisuus voittaa. Peli ei voi päättyä tasapeliin.
  • Yhden pisteen potkun todennäköisyys touchdownin jälkeen on 100 %.
  • Kahden pisteen muunnoksen todennäköisyys on p.

Millä p:n arvolla punaisen joukkueen pitäisi olla välinpitämätön potkuista ja kahden pisteen onnistumisyrityksestä ensimmäisen touchdownin jälkeen (nyt 8 pistettä tappiolla)?

anonyymi

(3-neliö(2))/2 = noin 0,381966011250105

Olkoon p = kahden pisteen muunnoksen ja potkun välinen indiferentiaalipiste.

Jos ensimmäinen kahden pisteen muunnosyritys onnistuu, punainen joukkue voi potkaista palloa toisen kerran ja voittaa.

Jos ensimmäinen kahden pisteen muunnosyritys epäonnistuu, punaisen joukkueen on yritettävä uudelleen toisen touchdownin jälkeen ja voitettava ottelu jatkoajalla.

Voiton todennäköisyys kahden pisteen potkaisuyrityksessä ensimmäisen touchdownin jälkeen on p + (1-p)*p/2. Verrataan tämä 50 %:n voittomahdollisuuteen potkaisemalla pallo ensimmäisen touchdownin jälkeen ja ratkaistaan p:n arvo.

p + (1 - p) * p / 2 = 1/2
2p + (1 -p)*p = 1
3p - p^2 = 1
p^2 - 3p + 1 = 0

Ratkaise p käyttämällä toisen asteen kaavaa:

p = (3 +/- neliöjuuri(5))/2

Otamme negatiivisen vaihtoehdon, jotta p pysyy 0:n ja 1:n välillä, jolloin saadaan p = (3-sqrt(2))/2 = apx. 0.381966011250105

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Edellisessä Kysy velholta -kolumnissa sinulta kysyttiin odotettavissa olevasta heittojen määrästä, jotta kahdella nopalla saadaan kahdesti peräkkäin yhteensä tulos 12. Samasta syystä foorumillasi joku väittää nähneensä 18 peräkkäistä nopanheittoa (yhteensä 11) craps-pöydässä. Mikä on odotettavissa oleva heittojen määrä, jotta se tapahtuisi?

anonyymi

41660902667961039785742

Tässä on ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Tarkka vastaus löytyi WizCalcin avulla.

Ruohikko on ympyrän muotoinen ja sen säde on 100 metriä. Sitä ympäröi pyöreä aita. Vuohi on kiinnitetty ketjulla koukkuun aidan kiinteässä kohdassa. Estääkseen vuohen liikalihavuuden maanviljelijä haluaa varmistaa, että se ylettää vain puoleen pellon ruohosta. Kuinka pitkä ketjun tulisi olla?

Havainnollistamiseksi ympyrä kuvaa nurmikenttää. S-kirjain edustaa paikkaa, johon ketju on kiinnitetty kentän reunassa. Ympyrän keltainen osa on kohta, johon vuohi yltää. Vihreä alue on ketjun ulottumattomissa. Tavoitteena on saada ketju oikealle etäisyydelle, jotta vihreä ja keltainen osa ovat yhtä pitkät.

vuohen kysymys

Gialmere

115,87286 metriä.

Katso seuraavaa kaaviota tämän ongelman ratkaisemiseksi.

vuohipalapeli

Piste Q on ruohoisen ympyrän keskipiste. Vuohen ketju on kiinnitetty pisteeseen R. Vuohi voi yltää kaikkiin väritettyihin alueisiin, mukaan lukien niiden peilikuvaan suoran PR alapuolella.

Sinulle on annettu, että ruohoisen ympyrän säde on 100, joten b + c = d = 100.

Ratkaisen tämän määrittelemällä kaiken b:n avulla. Sitten leikin b:llä, kunnes saavutan halutun tuloksen, jossa vuohi voi syödä puolet ruohosta.

Aloitetaan ratkaisemalla e b:n termillä. Tarkastellaan kolmiota, jonka sivut ovat b, d ja e, ja käytetään Pythagoraan kaavaa:

b^2 + e^2 = d^2
b^2 + e^2 = 10000
e = neliöjuuri(10000 - b^2)

Ratkaistaan seuraavaksi funktio f b:n avulla. Muista, että tiedämme jo b+c=100, joten c=100-b. Pythagoraan loitsua käyttäen:

c^2 + e^2 = f^2
(100 - b)^2 + (10000 - b^2) = f^2
f^2 = 10000 - 200b + b^2 + 10000 - b^2
f^2 = 20000 - 200b
f^2 = 100 * (200 - 2b)
f = 10*neliöarvo(200-2b)

Seuraavaksi lasketaan QRS-kolmion pinta-ala:

QRS = (1/2)*100*e = 50*neliöarvo(10000 - b^2)

Seuraavaksi etsitään nurmikon viipaleen pinta-ala leikattuna kulmalla SQR:

tan(neliö) = e/b = neliöjuuri(10000 - b^2)/b.

slice SQR = atan(sqrt(10000-b^2)/b)

Punainen alue on yhtä kuin viipale SQR miinus kolmiokulma QRS = 5000*atan(sqrt(10000-b^2)/b) - (1/2)*100*e = 50*sqrt(10000 - b^2).

Seuraavaksi etsitään sininen + vihreä + keltainen + violetti alue. Tätä varten meidän on löydettävä QRS-kulma.

tan(QRS) = e/c = neliöjuuri(10000 - b^2) / (100 - b)

kulma QRS = atan(sqrt(10000-b^2)/(100-b)).

Lisää siihen punainen alue, niin saamme puolet vuohen syötäväksi kelpaavasta kokonaispinta-alasta:

atan(sqrt(10000-b^2)/(100-b)) + 50*sqrt(10000 - b^2).

Kaksinkertainen määrä PR-viivan alapuolella olevalle osalle saadaksesi kokonaispinta-alan:

2*atan(sqrt(10000-b^2)/(100-b)) + 100*sqrt(10000 - b^2).

Ruohikkoisen alueen kokonaispinta-ala on 10 000*pi.

Nyt vain leiki b:n kanssa, kunnes saat vuohen syömäpinta-alan, joka on 5 000 * pi. Excelin goalseek-funktio on loistava tällaisiin ongelmiin. En tiedä, miten kukaan on onnistunut missään ennen taulukkolaskentaa.

Tätä menetelmää käyttämällä saat tulokseksi b = 32,867402.

Sieltä saadaan f = ketjun pituus = 115,8728598 metriä.

Tätä kysymystä on kysytty ja siitä keskusteltu foorumillani Wizard of Vegasissa .

Mikä on suositeltava aloitussana Wordlessa ?

anonyymi

Vastatakseni tähän tarkastelin ensin kunkin kirjaimen esiintymistiheyttä kussakin asemassa sallittujen Wordlen ratkaisujen luettelon perusteella.

Kirjainten tiheys Wordlessa

Kirje Kohta 1 Kohta 2 Kohta 3 Kohta 4 Kohta 5 Kokonais
A 141 304 307 163 64 979
B 173 16 57 24 11 281
C 198 40 56 152 31 477
D 111 20 75 69 118 393
E 72 242 177 318 424 1233
F 136 8 25 35 26 230
G 115 12 67 76 41 311
H 69 144 9 28 139 389
Minä 34 202 266 158 11 671
J 20 2 3 2 0 27
K 20 10 12 55 113 210
L 88 201 112 162 156 719
M 107 38 61 68 42 316
N 37 87 139 182 130 575
O 41 279 244 132 58 754
P 142 61 58 50 56 367
Q 23 5 1 0 0 29
R 105 267 163 152 212 899
S 366 16 80 171 36 669
T 149 77 111 139 253 729
U 33 186 165 82 1 467
V 43 15 49 46 0 153
Länsi 83 44 26 25 17 195
X 0 14 12 3 8 37
Y 6 23 29 3 364 425
Z 3 2 11 20 4 40

Sitten tarkastelin kaikkia Wordlen ratkaisulistalla olevia sanoja, joissa oli viisi eri kirjainta, ja pisteytin ne yllä olevan kirjainten esiintymistiheystaulukon mukaisesti. Annoin kaksi pistettä oikeassa paikassa olevasta osumasta ja yhden pisteen väärässä paikassa olevasta osumasta. Sitten lajittelin listan, jonka näet alla.

Parhaat aloitussanat Wordlessa

<!--/laatikon-otsikko-->
keskitetty">Pisteet
Sijoitus Sana
1 Tuijotus 5835
2 Nousi 5781
3 Liuskekivi 5766
4 Nosta 5721
5 Nouse 5720
6 Saner 5694
7 Virveli 5691
8 Raivostunut 5682
9 Tunkkainen 5665
10 Laatikko 5652
11 Jäljittää 5616
12 Myöhemmin 5592
13 Jakaa 5562
14 Kauppa 5547
15 Pelästyttää 5546
16 Muuttaa 5542
17 Nosturi 5541
18 Hälytys 5483
19 Kyynelteinen 5479
20 Paista 5475
21 Pitopalvelu 5460
22 Varaosa 5457
23 Yksin 5452
24 Kauppa 5449
25 Kuorsata 5403
26 Raastaa 5403
27 Liuske 5392
28 Vähiten 5390
29 Varasti 5377
30 Skaala 5376
31 Reagoi 5376
32 Pauhata 5368
33 Jäsentää 5351
34 Häikäisy 5340
35 Sovittaa 5338
36 Oppia 5324
37 Varhainen 5320
38 Kallistuva 5307
39 Vaaleampi 5285
40 Leimahdus 5280
41 Käytävä 5280
42 Ranta 5274
43 Varastaa 5268
44 Trice 5267
45 Pisteet 5258
46 Tyhjennä 5258
47 Emäntä 5253
48 Kivi 5253
49 Sydän 5252
50 Häviäjä 5251
51 Kartio 5248
52 Vihaaja 5243
53 Rele 5241
54 Levy 5240
55 Jumaloida 5239
56 Kastike 5236
57 Turvallisempi 5235
58 Ulkomaalainen 5233
59 Kasti 5232
60 Leikkaus 5231
61 Paalain 5230
62 Sireeni 5226
63 Kanootti 5215
64 Shire 5213
65 Munuaisten 5210
66 Kerros 5206
67 Kesyttäjä 5200
68 Suuri 5196
69 Helmi 5196
70 Reitti 5194
71 Ahdin 5192
72 Viipale 5178
73 Vaihe 5171
74 Proosa 5170
75 Itiö 5169
76 Herättää 5166
77 Armo 5164
78 Aurinko 5152
79 Sviitti 5150
80 Paisti 5145
81 Lager 5130
82 Lentokone 5129
83 Knappi 5129
84 Jaettu 5128
85 Keihäs 5126
86 Hienoa 5126
87 Aider 5123
88 Trooppi 5116
89 Torni5108
90 Kulutuspinta 5107
91 Orja 5097
92 Lähellä 5090
93 Lanssi 5090
94 Huuhtele 5088
95 Aiheuttaa 5087
96 Altis 5087
97 Drooni 5082
98 Melu 5079
99 Vaakuna 5073
100 Selvä 5068

Siinä se, suosittelemani aloitussana, jota itse käytän, on TUIJOITTAA.

Mikä on i^i

Aidan

e^(-pi/2) =~ 0.20788.

Tässä on ratkaisuni (PDF).

Haluat pelata peliä, jossa tarvitaan kaksi tavallista kuusisivuista noppaa. Valitettavasti hävisit nopan. Sinulla on kuitenkin yhdeksän indeksointikorttia, jotka voit merkitä haluamallasi tavalla. Pelaajan on valittava kaksi indeksointikorttia satunnaisesti yhdeksästä ilman takaisinpanoa ja laskettava kahden kortin summa.

Gialmere

Kortin arvojen ei tarvitse olla kokonaislukuja.

Merkitse kortit seuraavasti:

1 @ 0.5
1 @ 1.5
2 @ 2.5
1 @ 3.5
2 @ 4.5
1 @ 5.5
1 @ 6.5

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Onko totta, että reilu kolikko osuu todennäköisemmin kuvapuoli ylöspäin sille puolelle, joka alkoi kuvapuoli ylöspäin?

anonyymi

Todisteet viittaavat siihen, että tämä on totta!

Persi Diaconis ja Susan Holmes Stanfordin yliopistosta kirjasivat 10 000 kolikonheittoa. Kolikko laskeutui samalle puolelle ylöspäin kuin se oli alussa 50,8 % ajasta (lähde: The Fifty-one Percent Solution uutiskirjeestä What's Happening in the Mathematical Sciences, jonka on kirjoittanut American Mathematical Society). Todennäköisyys sille, että suhde on niin korkea tai suurempi, on 5,48 %.

Todistaakseni tämän matemaattisesti oletin, että kolikon todellinen kierrosten lukumäärä noudatti Poisson-jakaumaa. Tarkemmin sanottuna, jos kierrosten keskimääräinen lukumäärä oli m, niin täsmälleen n kierroksen todennäköisyys on exp(-m)*m^n/n!. Havainnollistaakseni Poisson-jakaumaa seuraava kaavio näyttää 0–25 kierroksen todennäköisyyden, kun keskiarvo on 10.

Valitsin Poissonin oletuksen siksi, että se noudattaa lähes kellokäyrän muotoa riittävän suurilla keskiarvoilla, eikä todellinen tulos voi koskaan laskea nollan alapuolelle.

Laskin sitten parillisen määrän puolikierroksia todennäköisyyden (jolloin kone laskeutuu samalle sivulle alaspäin kuin lähtöasennossa) eri puolikierrosten keskiarvoilla. Seuraava taulukko näyttää tulokset 0,5–5,0 keskiarvoilla.

Parillisen ja parittoman kierrosten lukumäärän todennäköisyys

Keskimääräiset vallankumoukset Tasapeli yhteensä Pariton kokonaissumma
0,5 0.567667642 0.432332358
1 0.509157819 0.490842181
1.5 0.501239376 0.498760624
2 0.500167731 0.499832269
2.5 0.500022700 0.499977300
3 0.500003072 0.499996928
3.5 0.500000416 0.499999584
4 0.500000056 0.499999944
4.5 0.500000008 0.499999992
5 0.500000001 0.499999999

Sitten aloin miettiä, miksi parillisen luvun todennäköisyys on aina suurempi kuin 50 %. Kävi ilmi, että parillisen luvun todennäköisyys, annettuna m:n keskiarvo, voidaan ilmaista muodossa 0,5 + e^(-2m)/2. e:n potenssiin minkä tahansa on oltava positiivinen, joten myös parillisen kierrosmäärän todennäköisyys on positiivinen.

Voit nähdä todistukseni tälle kaavalle täältä .

Ratkaise x:n arvo:

9 × + 12 × = 16 ×

anonyymi

=(log(1+neliöjäännösjäännös(5))-log(2))/(log(4)-log(3)) =~ 1.67272093446233.

Tässä on ratkaisuni (PDF).

Tätä ongelmaa kysyttiin ja siitä keskusteltiin foorumillani Wizard of Oddsissa .

Tämä ongelma sai inspiraationsa videosta Vaikea eksponentiaalinen kysymys .

Toimistossasi sadan työntekijän ryhmässä järjestetään salainen joulupukin lahjavaihto. Siinä kirjoitetaan kaikkien nimet yksittäisille paperilapuille, laitetaan ne hattuun ja jokainen arpoo satunnaisesti nimen, jolle hän antaa lahjan.

Kysymys kuuluu, kuinka monta suljettua silmukkaa keskimäärin on?

Esimerkki suljetusta silmukasta, jonka koko on 4: Gordon antaa Donille, Don antaa Jonille, Jon, joka antaa Nathanille, ja Nathan antaa Gordonille.

Oman nimen piirtäminen olisi suljettu silmukka, jonka koko on 1.

anonyymi

(1/1) + (1/2) + (1/3) + ... + (1/100) =~ 5.187377518.

Oletetaan, että Secret Santa -juhliin tulee vain yksi työntekijä. Hän tietenkin valitsee itsensä, joten kyseessä on yksi suljettu silmukka.

Sitten toinen työntekijä saapuu myöhässä ja pyytää päästä mukaan. He antavat hänelle listan nyt kahdesta työntekijästä. On puolet todennäköisyyttä, että hän valitsee työntekijän 1 ja toisen itse. Jos hän valitsee työntekijän 1, hänet voidaan puristaa hänen silmukkaansa, jossa hän ostaa työntekijälle 1 ja työntekijä ostaa hänelle. Joten nyt olemme tilanteessa 1 + 0,5 * 1 = 1,5

Sitten kolmas työntekijä saapuu myöhässä ja pyytää päästä mukaan. He antavat hänelle listan nykyisistä kolmesta työntekijästä. On 2/3 todennäköisyys, että hän valitsee työntekijän 1 tai 2 ja 1/3 itse. Jos hän valitsee työntekijän 1 tai 2, hänet voidaan puristaa heidän silmukkaan, jossa hän ostaa valitsemalleen työntekijälle ja se, jonka virallisesti piti ostaa kyseisen työntekijän puolesta, ostaa nyt kolmannelle. Joten nyt olemme tilanteessa 1,5 + (1/3) = 11/6.

Sitten neljäs työntekijä saapuu myöhässä ja pyytää päästä mukaan. He antavat hänelle listan nyt neljästä työntekijästä. On 3/4 todennäköisyyttä, että hän valitsee työntekijät 1–3 ja itse 1/4. Jos hän valitsee työntekijät 1–3, hänet voidaan puristaa heidän silmukkaan, jossa hän ostaa valitsemalleen työntekijälle ja se, jonka virallisesti piti ostaa kyseisen työntekijän puolesta, ostaa nyt neljälle. Joten nyt olemme tilanteessa 11/6 + (1/4) = 25/12.

Jatka näin, niin lopullinen vastaus on 1/1 + 1/2 + 1/3 + ... + 1/100 =~ 5.187377518.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Tarkastellaan puoliympyrää, jonka säde on 1 ja jonka sisällä on kaksi päällekkäin asetettua suorakulmiota. Mikä on näiden kahden suorakulmion suurin yhteenlaskettu pinta-ala?

kaksi suorakulmiota puoliympyrässä

anonyymi

sqrt(5)-1 =~ 1.236067977499790.

Tässä on koko ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Älä ota huomioon identtisiä kaksosia ja oleta, että jokaisella lapsella on 50/50 mahdollisuus syntyä pojaksi tai tytöksi. Jos lapset valitaan satunnaisesti 2–5 hengen perheistä, mikä on todennäköisyys, että pojalla tai tytöllä on sisar?

anonyymi

Mielenkiintoista kyllä, todennäköisyys on sama kummallakin sukupuolella perhekoosta riippumatta.

Tarkastellaan esimerkiksi kolmen hengen perheitä. Tässä on kahdeksan mahdollista tapaa järjestää pojat ja tytöt järjestyksen suhteen:

BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG

Jos valitset yllä olevasta listasta satunnaisesti minkä tahansa tytön, huomaat, että 12 tytöstä 9:llä on siskoja. Sama pätee 12 pojaan, 9:llä on siskoja. Todennäköisyys on siis 9/12 = 3/4.

Yleinen kaava todennäköisyydelle sille, että lapsella on sisar, kun lasten lukumäärä on n, on 1-(1/2) n-1 .

Tässä on sisaren todennäköisyys perheen lasten kokonaismäärän mukaan:

  • 1: 0
  • 2: 1/2
  • 3: 3/4
  • 4: 7/8
  • 5: 15/16
  • 6: 31/32

Vaihtoehtoisesti on järkevää, että todennäköisyys olisi sama pojille ja tytöille. Sisarustesi sukupuoli ei ole yhteydessä sinun sukupuoleesi. Näin ollen vain perheen koolla on merkitystä, ei omalla sukupuolellasi.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Survivorin 37. kauden 4. jaksossa oli haaste, jossa neljästä palapelistä piti koota sekä neliö että tasasivuinen kolmio. Mitkä olivat palojen tarkat mitat, jotta tämä toimisi?

lyhyttavarakauppa-aukio lyhyttavarakauppiaiden kolmio

anonyymi

Ensin tehdään kunnollinen kaavio ja nimetään se.

lyhyttavarakaupan ratkaisu neliö

Seuraava on vain ratkaistun kolmion kaavio.

lyhyttavaran ratkaisukolmio

Seuraavaksi, olettaen, että neliön sivut ovat pituudeltaan 1, tässä on vain kunkin kirjaimen pituus yllä olevassa kaaviossa.

[spoileri]

a = d = e = h = 1/2

b = g = SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0,572145321740575

c = f = 1-SQRT((4-SQRT(3))/(4*SQRT(3))) =~ 0,427854678259425

k = m = 1/neliöjyrä(neliöjyrä(3)) = ~ 0,759835685651592

n = (3-SQRT(4*SQRT(3)-3))/(2*SQRT(SQRT(3))) =~ 0,386767938902275

p = (SQRT(4*SQRT(3)-3)-1)/(2*SQRT(SQRT(3))) =~ 0,373067746749317

[/spoiler]

Lopuksi, tässä on täydellinen ratkaisuni (PDF).

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Olen varma, että olet Rillit huurussa -elokuvan fani. Yksi suosikkikohtauksistani on Kivi, paperi, sakset ja lisko Spock -peli. Se on kuin viiden symbolin kivi, paperi, sakset -peli, jossa on seuraavat säännöt:

  • Paperi peittää kiven
  • Kivi murskaa liskon
  • Lisko myrkyttää Spockin
  • Spock murskaa sakset
  • Sakset leikkaavat paperia
  • Lisko syö paperia
    • Spock höyrystää kiven
  • Sakset katkaisevat liskon pään
  • Paperi kumoaa Spockin väitteet
  • Kivi murskaa sakset

Kysymykseni kuuluu, voidaanko lisätä symboleja, jotta jokaisella osapuolella on samat mahdollisuudet satunnaista pelaajaa vastaan?

anonyymi

Kyllä, minäkin rakastan tuota kohtausta! Tässä on siitä YouTube-video .

Tarvitset parittoman määrän symboleja. Teoriassa niitä voisi olla parillinen määrä, mutta silloin pitäisi luoda säännöt, joiden mukaan tietyt eri symbolien parit johtaisivat tasapeliin. Ei, haluamme ratkaisevan pelin, jossa ainoat tasapelit ovat, jos molemmat pelaajat pelaavat saman symbolin.

Ratkaisu on erityisen elegantti ja helppo selittää alkuluvulla symboleja. Selitän esimerkkinä seitsemän symbolin avulla. Merkitään symbolit A:sta G:hen ja esitetään ne ympyrällä seuraavassa kaaviossa.

rps1

Aloita seuraavaksi kohdasta A ja piirrä sitten nuoli seuraavaan symboliin myötäpäivään. Nuolen tulee osoittaa kohti näiden kahden välistä olevaa kohtaa. Ajattele sitä kuin symbolia ammuttaisiin nuolella. Jatka myötäpäivään, kunnes pääset takaisin kohtaan A. Kaavio ei näytä tältä:

rps2

Tee seuraavaksi sama, mutta siirry kaksi symbolia myötäpäivään alkaen A:sta. Itse asiassa voit aloittaa mistä tahansa. Kaavio näyttää nyt tältä:

rps3

Tee lopuksi sama, mutta jätä kolme symbolia myötäpäivään väliin. Kaavio näyttää nyt tältä:

rps4

Huomaa tässä vaiheessa jokainen symboli voittaa kolme muuta symbolia ja kolme muuta eri symbolia voittaa sen.

Tämä menetelmä toimii mille tahansa alkuluvulle symboleja, koska kun palaat takaisin alkuperäiseen symboliin, olet käynyt läpi jokaisen symbolin. n symbolin kohdalla sinun on käytävä läpi tämä prosessi (n-1)/2 kertaa.

Voit tehdä tasapainoisen pelin millä tahansa parittolla määrällä symboleja, mutta joskus palaat takaisin alkuperäiseen symboliin liian nopeasti. Kun näin tapahtuu, sinun on tehtävä uusia silmukoita aloittaen niistä symboleista, jotka jäit huomaamatta.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Sekoitat normaalin (28 laatan) dominosetin ja nostat niistä yhden satunnaisesti. Paljastat varovasti toisen sivun, jolloin näkyviin tulee kuutonen. Mikä on todennäköisyys, että tämä on tuplakuutonen?

Gialmere

Niille, jotka eivät tunne dominoita, tiedoksi, että dominolla on kaksi sivua, joilla kummallakin on luku väliltä 0-6. Joukko koostuu yhdestä jokaisesta mahdollisesta dominosta. Se olisi kaikki combin(7,2)=21 tapaa valita numeroita seitsemästä vaihtoehdosta ilman takaisinpanoa, sekä kaikki seitsemän tapaa saada molemmat numerot samalla puolella.

Tässä ovat kaikki 28 niistä: 0-0, 0-1, 0-2, 0-3, 0-4, 0-5, 0-6, 1-1, 1-2, 1-3, 1-4, 1-5, 1-6, 2-2-2, 2-3, 2-4, 2-5, 2-6, 3-3, 3-4, 3-5, 3-6, 4-4, 4-5, 4-6, 5-5, 5-6, 6-6.

Kun tuo selitys on ohi, tässä ovat vastaus ja ratkaisu.

1/4 = 25%

Yksinkertainen tapa muotoilla kysymys on, mikä on todennäköisyys, että satunnaisesti valitulla dominolla on sama numero molemmilla puolilla. Vastaus on yksinkertaisesti 7/28 = 1/4.

 

Voisi sanoa, että vastauksen pitäisi olla 1/7, koska toinen puoli voisi olla mikä tahansa seitsemästä mahdollisesta luvusta. On totta, että se voisi olla mikä tahansa seitsemästä luvusta, mutta ne eivät kaikki ole yhtä todennäköisiä. Domino 6-6 pitäisi laskea kahdesti, koska siinä on kaksi sivua, joissa on kuutos. Joten toinen puoli voisi olla kumpi tahansa kahdesta kuutosesta ja joukossa on yhteensä kahdeksan kuutosia. Näin ollen vastaus on 2/8 = 1/4.

Tätä kysymystä on kysytty ja siitä keskustellaan foorumillani Wizard of Vegasissa . Kysymys on omistettu Alan Mendelsonin muistolle.

Alan ja Bob päättävät pelata tennistä, kunnes toinen heistä voittaa kaksi peliä peräkkäin. Alanin voiton todennäköisyys missä tahansa pelissä on 2/3. Mikä on todennäköisyys, että Alan voittaa turnauksen?

anonyymi

Alan ja Bob päättävät pelata tennistä, kunnes toinen heistä voittaa kaksi peliä peräkkäin. Alanin voiton todennäköisyys missä tahansa pelissä on 2/3. Mikä on todennäköisyys, että Alan voittaa turnauksen?

Vastaus on 16/21 = 76,1905%.

 

Seuraava on generointiratkaisu mille tahansa Alanin voittotodennäköisyydelle yksittäisessä pelissä.

Olkoon p = todennäköisyys a voittaa.
Olkoon a = todennäköisyys, että Alan voittaa turnauksen Alanin voitettua edellisen pelin.
Olkoon b = todennäköisyys, että Alan voittaa turnauksen Bobin voitettua edellisen pelin.

(1) a = p + (1 - p) * b
(2) b = p*a

Yhtälön (2) sijoittaminen yhtälöön (1):

a = p + (1 - p) * pa
a = p + pa - p² * a
a - pa + p 2 *a = p
a(1 - p + p² ) = p
(3) a = p/(1 - p + p² )

Yhtälön (3) sijoittaminen yhtälöön (2):

b = p² /(1 - p + p² )

Ensimmäisessä pelissä ratkaistaan, onko turnauksen voittamisen todennäköisyys a vai b:

vastaus = pa + (1-p)b
= p² /(1 - p + p² ) + (1 - p) * p² /(1 - p + p² )
= ( 2a² -a³ )/( a² -a+1)

Jos a=2/3, turnauksen voittotodennäköisyydeksi saadaan 16/21.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .

Sinulla on 1,5 metrin korkuiset tikkaat. Haluat nojata ne seinää vasten mahdollisimman korkealle. On kuitenkin olemassa 1x1x1 kuutiojalan laatikko, jonka yli sinun on asetettava tikkaat. Et voi siirtää laatikkoa. Mikä on tikkaiden yläreunan enimmäiskorkeus?

anonyymi

Vastaus on (1 + neliö(26) - neliö(23-2*neliö(26)))/2 =~ noin 4,838501 jalkaa.

Tässä on ratkaisuni (PDF).

Millä arvolla x 1/x on maksimissaan?

anonyymi

Vastaus on e = ~ 2,71828182845905.

Siinä e^(1/e):n arvo on ~ 1,44466786100977.

Tässä on ratkaisuni (PDF).

Vuoden 1944 sanomalehdet huomasivat tämän uskomattoman sattuman:

sattuma

Onko tämä suuri sattuma vai onko kyseessä jokin matemaattinen kikka?

Gialmere

Se on matemaattinen kikka ja tunnetun taikatempun perusta.

Jokaisen vuonna 1944 elossa olleen iän (syntymäpäivän jälkeen) ja syntymävuoden summa oli 1944. Ajattelepa tätä. Jos olit x vuotta vanha, niin syntyit vuonna 1944-x. Summa on x + (1944-x) = 1944.

Se on sama asia kuin "virkavuodet" vuonna 1944. Jos olit virassa y vuotta, sinun on täytynyt aloittaa vuosina 1944-y. y + (1944-y) = 1944.

Summa 1944 + 1944 = 3 888. Toimii joka kerta.

Jotta tästä tulisi toimiva taikatemppu vuonna 2023, lasketaan yhteen seuraavat neljä asiaa:

  1. Heidän syntymävuotensa
  2. Kuinka vanhoja he täyttävät tänä vuonna.
  3. Vuosi, jolloin jokin merkittävä tapahtuma sattui (kuten ensimmäisen lapsen syntymä).
  4. Tuon merkittävän tapahtuman vuosipäivä tänä vuonna.

Se on aina summa 2023 + 2023 = 4046.

Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .