Todennäköisyys - Pulmapelit
Olen kiinnostunut selvittämään hieman tarkempaa tietoa nopanheiton todennäköisyyksistä. Jos sinulla on kuusi noppaa ja heität ne kaikki kerralla, kaikkien ykkösten heiton todennäköisyys on 1:46 656. Kysymykseni kuuluu, mikä on todennäköisyys heittää yhdestä viiteen ykköstä. Olen todella kiinnostunut selvittämään kaavan, jota tulisi käyttää tällaisen ongelman laskemiseen.
Todennäköisyys saada x ykköstä y nopasta on combin(y,x)*(1/6) x *(5/6) yx . Katso combin(x,y)-funktion selitys pokerin todennäköisyyksiä käsittelevästä osiostani. Esimerkiksi neljän ykkösen heiton todennäköisyys on combin(6,4)*(1/6) 4 *(5/6) 2 = 0,803755%.
Ykkösten lukumäärä kuudessa nopassa
| Ykköset | Todennäköisyys |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0,0535837 |
| 4 | 0,0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| Kokonais | 1.0000000 |
Kahdeksan golfaajaa meni uudelle kentälle. Caddymaster laittoi kahdeksan bägiä neljälle satunnaisesti valitulle kärrylle. Pelaajat laittoivat kahdeksan merkittyä golfpalloa hattuun. Pallot heitettiin ilmaan. Kaksi toisiaan lähimpänä olevaa palloa olivat pareja. Jokaisessa tapauksessa parien golfbägit olivat jo samalla kärryllä. Mikä on todennäköisyys sille, että golfbägit oli paritettu oikein ennen heittoa?
Yhdistelmien lukumäärän kaavamainen vastaus olisi combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105. Toinen tapa ratkaista yhdistelmien lukumäärä olisi valita yksi golfaaja satunnaisesti. Hänen kanssaan voidaan parittaa seitsemän henkilöä. Sitten valitaan toinen golfaaja satunnaisesti kuudesta jäljellä olevasta. Hänen kanssaan voidaan parittaa viisi henkilöä. Sitten valitaan toinen golfaaja satunnaisesti neljästä jäljellä olevasta. Hänen kanssaan voidaan parittaa kolme henkilöä. Joten yhdistelmien lukumäärä on 7*5*3 = 105. Vastaus on siis 1/105.
Ystäväni lähetti minulle tämän , ja mietin, onko olemassa kaavaa, miten tämä toimii.
Usein nämä ajatustenlukupulmat toimivat mielenkiintoisen matemaattisen erikoisuuden vuoksi. Jos luvun numeroiden summa on jaollinen 9:llä, niin luku itse on jaollinen 9:llä. Kokeillaanpa tätä Las Vegas Tropicanan puhelinnumerolla (702-739-2222). Numeroiden summa on 7+0+2+7+3+9+2+2+2+2 = 36. Luku 36 on tasan jaollinen 9:llä, joten luvun 702739222 täytyy myös olla jaollinen 9:llä. Tässä on todiste tästä.
- Olkoon n mikä tahansa kokonaisluku. Ilmaise n muodossa d 0 *1 + d 1 *10 + d 2 *100 + d 3 *1000 + ... + d n *10 n , jossa d n on ensimmäinen numero, d n - 1 on toinen ja niin edelleen.
- n = [d 0 + d 1 + d 2 + ... + d n ] + [d 1 *9 + d 2 *99 + d 3 *999 + ...+ d n *999...9 (luku, jossa on n yhdeksikköä)]
- n = [d 0 + d 1 + d 2 + ... + d n ] + 9*[d 1 *1 + d 2 *11 + d 3 *111 + ... d n *111...1 (luku, jossa on n ykköstä)]
- 9*mikä tahansa kokonaisluku on tasan jaollinen 9:llä. Joten jos d 0 + d 2 + d 2 + ... + d n eli numeroiden summa on jaollinen 9:llä, niin koko luvun on oltava jaollinen 9:llä.
Nyt kun todistus on selvitetty, voimme tarkastella tätä taikatemppua. Tehtävässä sinua pyydetään valitsemaan mikä tahansa luku. Sitten järjestämään numerot uudelleen muodostaaksesi toisen luvun. Sitten vähentämään pienempi luku suuremmasta luvusta.
Vastauksessa on aina yhdeksällä jaollinen numeroiden summa. Miksi? Jokainen alkuperäisen luvun numero esiintyy jossain muualla toisessa luvussa. Käymällä numerosarjaa yksi kerrallaan ja muuttamalla kaikki muut numerot nollaksi, voisimme tiivistää jokaisen sarjan muotoon +/- n * [10 x - 10 y ] (missä x > = y ja n on numero) = +/- n * 10 y * (10 xy - 1) = 10 y * (luku, joka koostuu vain yhdeksistä) = luku, joka on jaollinen yhdeksällä.
Katsotaanpa esimerkkiä. Olkoon alkuperäinen luku 1965. Sekoita se ylös saadaksesi 6951. 6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999. Huomaa, että jokainen osa on jaollinen 9:llä, joten vähennyslaskun jälkeen saamasi luvun on myös oltava jaollinen 9:llä, ja lopuksi numeroiden summa on myös jaollinen 9:llä.
Temppu pyytää sinua sitten ympyröimään jonkin muun luvun kuin nollan ja syöttämään kaikkien muiden numeroiden summan. Ohjelman tarvitsee sitten vain lisätä antamaasi lukuun luku, jotta summa on jaollinen 9:llä. Jos esimerkiksi sanoit, että numeroidesi summa on 13, sinun on täytynyt ympyröidä luku 5, koska 13 + 5 = luku, joka on jaollinen 9:llä.
Syy siihen, miksi et voi ympyröidä nollaa, on se, että jos ympyröisit ja sitten syöttäisit luvun, joka on jo jaollinen 9:llä, ohjelma ei tietäisi, ympyröitkö luvun 0 vai 9.
Hieno sivusto. Kutsun sitä usein uhkapelurina, joka on kiinnostunut todennäköisyyksistä ja tilastoista, mutta tämä kysymys liittyy itse asiassa työhöni. Henkilöstöosastoni vaatii, että arvioin pienen henkilöstöni (5 henkilöä) kellokäyrän avulla – yksi 5 %:n parhaimmasta joukosta kaikista työntekijöistä, yksi seuraavien 20 %:n joukosta, yksi seuraavien 50 %:n joukosta, yksi seuraavien 20 %:n joukosta ja yksi 5 %:n heikoimmasta joukosta. Yrityksessä on noin 5000 työntekijää. Mikä on todennäköisyys, että näin pieni otoskoko sopii tähän jakaumaan?
Kiitos kehusta. Tämä on hyvä tehtävä. Todennäköisyys sille, että tasan yksi työntekijä kuuluu alimpaan 5 prosenttiin, on 5*(.05)*(.95) ⁴ = 0.203627. Olettaen, että yksi työntekijä kuuluu alimpaan 5 prosenttiin, todennäköisyys sille, että tasan yksi kuuluu seuraaviin 20 prosenttiin, on 4*(.2/.95)*(.75/.95) ⁴ = 0.414361. Jos nämä kaksi alisuoriutunutta työntekijää ovat todennäköisyys sille, että tasan yksi kuuluu seuraaviin 50 prosenttiin jäljellä olevista 75 prosentista, on 3*(.5/.75)*(.25/.75) ⁴ = 0.222222. Todennäköisyys sille, että toinen jäljellä olevista kahdesta kuuluu 25 prosentista alempaan 20 prosenttiin, on 2*(.2/.25)*(.05/.25) = 0.32. Kaikkien näiden todennäköisyyksien tulon tulokseksi saadaan 0,006 eli 3/5 yhdestä prosentista.
Tilaustilastoja ( sarake #100 ) kysyneelle kaverille minulla on kaksi ongelmaa: yksi pieni ja yksi suuri. Menetelmäsi ei onnistunut tekemään äärellisen populaatiokorjausta, mikä on myönnettävästi triviaalia 5000 työntekijän tapauksessa, mutta se ei varmasti olisi ollut mahdollista, jos työntekijöitä olisi ollut 20!
Vielä tärkeämpää on kuitenkin se, että oletat implisiittisesti, että johtajilla ei ole vaikutusta työntekijöihinsä. Oletetaan, että hyvät johtajat nostavat työntekijöidensä keskimääräistä tasoa harkitun palkkaamisen ja irtisanomisen tai keskimääräistä parempien motivointitaitojen avulla. Ilman tämän vaikutuksen huomioon ottamista vääristämme tuloksena olevia todennäköisyyksiä joko ylöspäin tai alaspäin. Olen varma, että tiesit tämän, mutta olen herkkä sille, koska teen paljon tällaisia laskelmia syrjintätapauksissa, ja se, että emme ota huomioon asioita, joihin voimme ottaa huomioon (tässä tapauksessa ryhmäkohtainen vaikutus), voi usein johtaa ihmisiä harhaan.
Kiitos hyvistä näkökohdista. Vaihtoehto työsuoritusarviointien jakautumisen hallitsemattomuudelle on kuitenkin arviointien inflaatio. Esimies joutuu antamaan paisuneita arvioita pitääkseen henkilökuntansa tyytyväisenä. Työskenneltyäni valtion virkailijana kymmenen vuotta minulla on tästä jonkin verran kokemusta. Kun opetin UNLV:ssä, ei ollut keskimääräistä luokka-arvosanaa, mutta oli tiettyjä odotuksia siitä, miltä arvostelukäyrän tulisi näyttää lukukauden lopussa. Ainakin korkeakouluympäristössä ajattelin, että se oli järkevä käytäntö. Ehkä myös liiketoimintaympäristössä jonkinlainen maalaisjärkinen toimintatapa olisi paras.
Onko olemassa pelimatemaatikkojen kohtaamia kuuluisia ratkaisemattomia ongelmia? Kuten Fermat'n viimeinen lause uhkapelimaailmassa. Jos on, voisitko jakaa esimerkin.
Hyvä kysymys. En keksi yhtäkään.
Miten tämä toimii: www.1800gotjunk.com/genie/ ?
Ilmaistaan lukusi muodossa 10t+u. Sinua pyydetään vähentämään jokainen numero, jolloin jäljelle jää 10t+utu = 9t, luku, joka on jaollinen 9:llä. Huomaa, kuinka kaikilla 9:llä jaollisilla luvuilla on sama alkio, joka on se, jonka henki ennustaa.
Olen menossa ammattitutkintoon. Säännökset määräävät, että:
- Kokeen tulee koostua seitsemästä aiheesta.
- Jokaisesta aiheesta on 60 monivalintakysymystä.
- Jokaisessa monivalintakysymyksessä on neljä mahdollista vastausta, mutta vain yksi oikea vastaus.
- Läpäisyyn vaaditaan vähintään 75 prosentin keskiarvo, eikä hänen arvosanansa saa olla missään aineessa alle 65 prosenttia.
Kysymykseni kuuluu, jos kokeeseen osallistuja vain arvaa kaikki vastauksensa, mitkä ovat hänen mahdollisuutensa läpäistä koe? Toisin sanoen, mikä on todennäköisyys läpäistä koe pelkällä tuurilla?
Täyttääkseen 75 %:n vaatimuksen opiskelijan on saatava vähintään 315 oikein 420 kysymyksestä. Odotettu oikeiden vastausten määrä arvaamalla on 420 * 0,25 = 105. Keskihajonta on (420 * 0,25 * 0,75)^0,5 = 8,87412. Joten ehdokkaan on ylitettävä odotukset 210 kysymyksellä eli 210 / 8,87412 = 23,66432 keskihajonnalla. Tämän todennäköisyys on uskomaton. Jos jokainen elävä olento maapallolla tekisi tämän testin vastaamalla satunnaisesti, epäilen, että kukaan tai mikään läpäisisi sen. En edes ryhdy toiseen vaatimukseen.
Jos yliopiston jalkapallojoukkueella on 10 %:n mahdollisuus voittaa ensimmäinen peli ja 30 %:n mahdollisuus voittaa toinen peli ja 65 %:n mahdollisuus hävitä molemmat pelit, mitkä ovat heidän mahdollisuutensa voittaa tasan yksi peli?
Jos olettaisimme pelien olevan toisistaan riippumattomia, molempien pelien häviämisen todennäköisyys olisi 90 % * 70 % = 63 %. Mutta koska sanot molempien pelien häviämisen todennäköisyyden olevan itse asiassa 65 % (mikä on enemmän kuin 63 %), se tarkoittaa, että tapahtumat korreloivat keskenään. Jos molempien pelien häviämisen todennäköisyys on 65 % ja pelkästään pelin 2 häviämisen todennäköisyys on 70 %, niin pelin 1 ja pelin 2 voittamisen todennäköisyyden on oltava 5 %. Samaa logiikkaa käyttäen pelin 1 ja pelin 2 häviämisen todennäköisyyden on oltava 25 %. Jäljelle jää vain 5 % molempien pelien voittamiselle. Joten todennäköisyys voittaa tasan kerran on 25 % + 5 % = 30 %.
Peliohjelmassa Let's Make a Deal on kolme ovea. Oletetaan esimerkiksi, että kahdesta ovesta paljastuu vuohi ja yhdestä uusi auto. Juontaja Monty Hall valitsee kaksi kilpailijaa valitsemaan oven. Joka kerta, kun Monty avaa ensin oven, jossa on vuohi. Oletetaan, että tällä kertaa se kuului ensimmäiselle kilpailijalle. Vaikka Monty ei koskaan itse asiassa tehnyt tätä, entä jos Monty tarjoaisi toiselle kilpailijalle mahdollisuuden vaihtaa ovea tässä vaiheessa toiseen avaamattomaan oveen. Pitäisikö hänen vaihtaa?
Kyllä! Tämän ongelman ydin on se, että isäntä on ennalta määrätty avaamaan ovi vuohella. Hän tietää, missä ovessa auto on, joten riippumatta siitä, mitkä ovet pelaajat valitsevat, hän voi aina paljastaa ensin vuohen. Kysymys tunnetaan nimellä "Monty Hallin paradoksi". Suuri osa hämmennyksestä johtuu siitä, että usein kysymystä muotoiltaessa ei virheellisesti tehdä selväksi, että isäntä tietää, missä auto on, ja paljastaa aina ensin vuohen. Mielestäni osa syystä on Marilyn Vos Savantin , joka muotoili kysymyksen huonosti kolumnissaan, niskoilla. Oletetaan, että palkinto on oven 1 takana. Seuraavassa on, mitä tapahtuisi, jos pelaajalla (toisella kilpailijalla) olisi strategiana olla vaihtamatta ovea.
- Pelaaja valitsee oven 1 --> pelaaja voittaa
- Pelaaja valitsee oven 2 --> pelaaja häviää
- Pelaaja valitsee oven 3 --> pelaaja häviää
Seuraavassa on, mitä tapahtuisi, jos pelaajalla olisi vaihtostrategia.
- Pelaaja valitsee oven 1 --> Isäntä paljastaa vuohen oven 2 tai 3 takana --> pelaaja vaihtaa toiselle ovelle --> pelaaja häviää
- Pelaaja valitsee oven 2 --> Isäntä paljastaa vuohen oven 3 takana --> pelaaja vaihtaa ovelle 1 --> pelaaja voittaa
- Pelaaja valitsee oven 3 --> Isäntä paljastaa vuohen oven 2 takana --> pelaaja vaihtaa ovelle 1 --> pelaaja voittaa
Joten vaihtamatta jättämisellä pelaajan voittomahdollisuudet ovat 1/3. Vaihtamalla pelaajan voittomahdollisuudet ovat 2/3. Joten pelaajan kannattaa ehdottomasti vaihtaa.
Lisätietoa Monty Hallin paradoksista voi lukea Wikipedian artikkelista.
Olen eri mieltä vastauksestasi Monty Hallin kysymykseen 19. marraskuuta 2004 julkaistussa kolumnissa. Olettaen, että auto on oven yksi takana, on itse asiassa neljä mahdollisuutta seuraavasti, joissa palkinto on oven yksi takana.
- Pelaaja valitsee oven 1 --> näytetään 2 --> vaihda oveen 3, häviä
- Pelaaja valitsee oven 1 --> näytetään 3 --> vaihda oveen 2, häviä
- Pelaaja valitsee oven 2 --> näytetään 3 --> vaihda oveen 1, voita
- Pelaaja valitsee oven 3 --> näytetään 2 --> vaihda oveen 1, voita
Kuten näet, voittotodennäköisyys on 50 % riippumatta siitä, vaihdatko peliä vai et. Lisäksi on vain järjen vastaista ajatella, että vaihtaminen olisi parempi vaihtoehto.
Virheesi on olettaa, että jokaisella näistä tapahtumista on 25 %:n todennäköisyys. Seuraavassa on kunkin tapahtuman oikea todennäköisyys.
- Pelaaja valitsee oven 1 (1/3) * näytetty 2 (1/2) = pelaaja häviää (1/6)
- Pelaaja valitsee oven 1 (1/3) * näytetty 3 (1/2) = pelaaja häviää (1/6)
- Pelaaja valitsee oven 2 (1/3) * näytetty 3 (1/1) = pelaaja voittaa (1/3)
- Pelaaja valitsee oven 3 (1/3) * näytetty 2 (1/1) = pelaaja voittaa (1/3)
Joten häviävien tapahtumien kokonaistodennäköisyys on 2*(1/6) = 1/3 ja voittavien tapahtumien kokonaistodennäköisyys on 2*(1/3)=2/3.
Viidellä eri täytteellä, kuinka monta erilaista pizzaa voit tehdä millä tahansa täytteiden määrällä?
On yksi tapa ilman täytettä, viisi tapaa yhdellä täytteellä, 10 tapaa kahdella täytteellä, 10 tapaa kolmella täytteellä, 5 tapaa neljällä täytteellä ja yksi tapa viidellä täytteellä. Vastaus on siis 1 + 5 + 10 + 10 + 5 + 1 = 32. Toinen ratkaisutapa on, voidaanko täytteitä käyttää tai ei. Loppusumma on siis 2,5 = 32.
Näin viime viikolla lehdessä, että viimeisin Indonesiaa ravistellut maanjäristys iski 26. joulukuuta. Siinä myös kerrottiin, että kahdeksasta tuhoisimmasta maanjäristyksestä viimeisen 100 vuoden aikana kolme on tapahtunut 26. joulukuuta. Mietin, mitkä ovat todennäköisyydet sille, että samana päivänä tapahtuu kolme valtavaa maanjäristystä, kun otetaan huomioon nämä tosiasiat: Tämän magnitudin maanjäristyksiä (8,0 tai suurempia) tapahtuu vain kerran vuodessa. Viimeisin suuri maanjäristys oli tasan vuosi sitten, 26.12.2003 Iranissa (peräkkäiset todennäköisyydet?). Odotan innolla yhteydenottoasi.
Saatuaani selville väitteen, jonka mukaan Floridan hurrikaanit iskivät vain Bushin äänestyspiirikuntiin, oli huijaus (ks. 17. lokakuuta 2004 julkaistu kolumni), aion suhtautua skeptisemmin tällaisiin väitettyihin sattumiin. National Earthquake Information Centerin mukaan 11 suurimmasta maanjäristyksestä vuoden 1990 jälkeen vain viimeisin, vuonna 2004 tapahtunut, iski 26. joulukuuta. Mainitsemasi Iranin maanjäristys oli voimakkuudeltaan vain 6,7 magnitudia, mikä on kaukana kahdeksan suurimman joukossa olemisesta.
Kuinka monta munaa sinulla on aluksi, jos myyt joka päivä puolet munista plus puolet jokaisesta munasta; kolmen päivän kuluttua sinulla ei ole yhtään munaa? Kunkin päivän lopussa munien lukumäärä on kokonaisluku.
Olkoon d (päivä) munien lukumäärä päivän alussa ja n (yö) munien lukumäärä päivän lopussa. Tehtävästä käy ilmi, että d/2 - ? = n. Ratkaistaan siis d n:n avulla.
d/2 = n + ?
d = 2n + 1
Joten kolmantena päivänä n=0, joten d=1.
Toisena päivänä n=1, joten d=3.
Kolmantena päivänä n=3, joten d=7.
Eli siinä se, aloitit seitsemällä munalla.
Kuvittele saari, jolla asuu 10 ihmistä, ja poliittinen tilanne on sellainen, että joka päivä yksi saarelainen valitaan sattumanvaraisesti päälliköksi täsmälleen yhdeksi päiväksi; päivän kuluttua valitaan sattumanvaraisesti toinen saarelainen (joten samalla saarelaisella, joka oli juuri päällikkö, on 1/10 mahdollisuus olla päällikkö uudelleen). Ratkaistava kysymys on: kuinka monta päivää keskimäärin pitäisi kulua ennen kuin jokainen saarelainen olisi ollut päällikkö ainakin kerran?
Yhden henkilön toimiminen päällikkönä vie vain yhden päivän. Toisena päivänä uuden päällikön todennäköisyys on 0,9. Uuden päällikön saamiseen kuluvien päivien odotusarvo, jos kunkin päivän todennäköisyys on 0,9, on 1/0,9 = 1,11. Tämä pätee kaikille todennäköisyyksille: odotettu kokeiden määrä onnistumiseen on 1/p. Joten kun kaksi henkilöä on palvellut, uuden päällikön todennäköisyys seuraavana päivänä on 0,8. Kolmannen päällikön odotusaika on siis 1/0,8 = 1,25 päivää. Vastaus on odotusaikojen summa, joka on 1/1 + 1/,9 + 1/,8 + ... + 1/,1 = 29,28968 päivää.
Ympyrän säde on 1. Kolmio on tasasivuinen. Laske kunkin värillisen alueen pinta-ala.
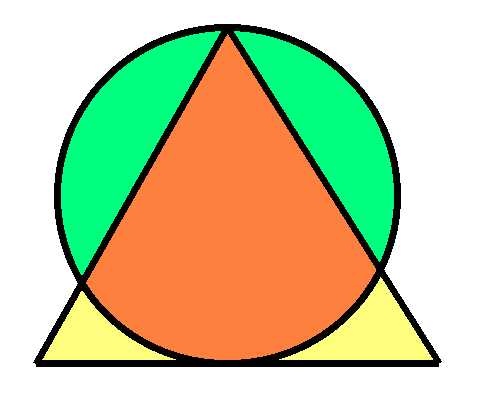
En halua paljastaa vastausta niille, jotka haluavat ratkaista sen itse. Vastauksen ja ratkaisun löydät toiselta verkkosivustoltani mathproblems.info , tehtävästä 189.
Oletetaan, että voitat ottelun, jossa NBA-ottelun puoliajalla saat heittää vapaaheiton ja jos onnistut, voitat miljoona dollaria. Lisäksi voit jatkaa vapaaheittojen heittämistä, tuplana tai ei ollenkaan, kunnes epäonnistut tai päätät lopettaa. Jos olet 75 %:n vapaaheittojen heittäjä, milloin lopettaisit? Voitko koskaan? Jossain vaiheessa raha alkaa merkitä yhä vähemmän ja vähemmän. Mitä tekisit?
Jossain vaiheessa kannattaa kieltäytyä hyvästä vedosta, koska panokset ovat liian korkeat. Henkilökohtaisesti mielestäni hyvä mittari rahasta saatavalle nautinnolle on summan logaritmi. Logarin kantaluvulla ei ole väliä, joten käytetään lukua 10. Emme kuitenkaan voi ottaa alle 10:n logaritmia, joten oletetaan, että nautinto on 0 alle kymmenen:n summalla. Oletetaan esimerkissäsi, että sinulla on 0 dollaria ennen kuin voitat 1 000 000 dollaria ensimmäisellä heitollasi. Nyt sinulla on log(1 000 000) = 6 onnellisuusyksikköä. Onnellisuutesi odotusarvo toisella vapaaheitolla on 0,75 * log(2 000 000) + 0,25 * 0 = 4,975772. Tämä on alle 6, joten tässä tapauksessa sinun pitäisi ottaa miljoona ja kävellä. Tilanne voi kuitenkin olla erilainen, jos sinulla on jo rahaa. Oletetaan, että sinulla on jo 200 000 dollaria. Tällöin onnellisuutesi kävelemällä on log(1 200 000) = 6,07918. Onnellisuutesi miljoonan riskeeraamalla ja ottamalla toisen mahdollisuuden on 0,75 * log(2 200 000) + 0,25 * log(200 000) = 6,082075, joten otat niukasti toisen mahdollisuuden. Jos voittaisit sen, valintasi olisi log(2 200 000) = 6,34242 ja 0,75 * log(4 200 000) + 0,25 * log(200 000) = 6,29269 välillä. Tässä tapauksessa sinun ei pitäisi ottaa kolmatta mahdollisuutta ja sen sijaan kävellä 2 000 000 dollarin voitolla. Ensimmäisen tuplauksen hyväksymisen kannattavuusraja on 191 487 dollarin olemassa oleva varallisuus. Kahden tuplauksen hyväksymiseksi sinulla pitäisi olla 382 975 dollaria muuta rahaa.
Muistan, että jos huoneessa on 22 ihmistä, on parillinen todennäköisyys sille, että kahdella heistä on sama syntymäpäivä [kuukausi ja päivä, ei vuosi]. Olen unohtanut, miten tämä todistetaan laskemalla. Voisitko kertoa sen?
Luulen vastanneeni tähän aiemmin, mutta 50/50-kohta on lähempänä lukua 23. Yksinkertaisuuden vuoksi jätetään karkausvuodet huomiotta. Pitkä vastaus on järjestää 23 henkilöä jotenkin järjestykseen. Todennäköisyys sille, että henkilöllä #2 on eri syntymäpäivä kuin henkilöllä #1, on 364/365. Todennäköisyys sille, että henkilöllä #3 on eri syntymäpäivä kuin henkilöillä #1 ja #2, olettaen, että he ovat eri syntymäpäivät, on 363/365. Toista tätä, kunnes henkilö on 23. Todennäköisyys on siis (364/365)*(363/365)*...*(343/365) = 49,2703%. Joten todennäköisyys sille, ettei löydy osumaa, on 49,27 % ja että ainakin yksi osuma löytyy, on 50,73 %. Toinen ratkaisu on jakamalla 23 eri syntymäpäivän permutaatioiden lukumäärä niiden tapojen kokonaismäärällä, joilla voidaan valita 23 satunnaislukua väliltä 1–365, saadaan permut (365,23) / 365 23 = 42 200 819 302 092 400 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 / 85 651 679 353 150 300 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 = 49,27 %.
Erään osavaltion opettajien viikkopalkat noudattavat normaalijakaumaa, jonka keskiarvo on 490 dollaria ja keskihajonta 45 dollaria. Mikä on todennäköisyys, että satunnaisesti valittu opettaja ansaitsee yli 525 dollaria viikossa? En muista, miten todennäköisyys lasketaan pelkästään keskiarvosta ja keskihajonnasta ilman populaatiota.
Se olisi 35 dollaria keskiarvoa suurempi eli 7/9 keskihajontaa. Todennäköisyys sille, että tulos olisi yli 7/9 keskihajontaa odotettua suurempi, olisi 1 - Z(7/9) = 1 - 0,78165 = 0,21835.
Kaksi ihmistä pelaa kivi-paperi-sakset-peliä. Pelin oletetaan olevan strategiapeliä. Jos pelaat "paras kolmesta" -peliä ja pelaaja A voittaa ensimmäisen kierroksen, mitkä ovat todennäköisyydet sille, että pelaaja B voittaa pelin?
Pelaajan B pitäisi voittaa kaksi seuraavaa peliä (tasapelejä ei lasketa), joten todennäköisyys on (1/2) * (1/2) = 1/4.
Hei, ajattelin kysyä sinulta tätä, koska en löydä vastausta mistään netistä. Toivon, että vastaat tähän: Mitkä ovat olemassaolon todennäköisyydet? Olipa kyseessä sitten Maapallo tai jokin muu paikka maailmankaikkeudessa? Se ei ole uhkapelikysymys, vaan vastaus, joka meidän kaikkien tulisi tietää, jotta voimme ymmärtää, millaisia todennäköisyyksiä voitamme jo eläessämme!
Uskon, että älykkään elämän esiintymisen todennäköisyys missä tahansa galaksissa on erittäin korkea. Draken yhtälö pyrkii arvioimaan älyllisen elämän esiintymisten määrää galaksissa, ja laskelmista riippuen luku on noin miljoona. Ei kuitenkaan ole myöskään hyviä todisteita siitä, että nämä sivilisaatiot olisivat koskaan vierailleet luonamme tai olleet yhteydessä meihin. Niinpä kuuluisa Fermin kysymys kuuluu: "Missä kaikki ovat?" Mielestäni todisteiden puute muusta älykkäästä elämästä herättää epäilyksiä Draken yhtälöstä, mutta laskisin silti älykkäiden sivilisaatioiden määrän galaksissamme noin 1000:een. Se on vain meidän galaksimme, galakseja on miljardeja. Galaksien välinen etäisyys on kuitenkin niin suuri, ettei niiden välisestä matkustamisesta tai kommunikoinnista ole juurikaan hyötyä keskustella. Joten vastauksena kysymykseesi sanoisin, että noin 99,9 %.
Oletetaan, että hotellissa on 10 000 000 huonetta ja 10 000 000 elektronista avainta. Tietokonevirheen vuoksi jokaiseen avaimeen on ohjelmoitu satunnainen koodi, jonka todennäköisyys olla oikea on 1/10 000 000. Hotelli on loppuunmyyty. Mikä on todennäköisyys, että ainakin yhdellä asiakkaalla on toimiva avain?
Tarkka vastaus 1-(9 999 999/10 000 000) 10 000 000 = 0,632121. Tämä on myös sama kuin (e-1)/e seitsemän desimaalin tarkkuudella.
Kokeessa on 75 monivalintakysymystä. Jokaisessa kysymyksessä on neljä mahdollista vastausta, joista vain yksi on oikein. Kokeen läpäisyraja on 50 %. Mitkä ovat mahdollisuudet läpäistä koe arvaamalla jokaisen vastauksen?
1/635 241.
Jos tennispelaajalla on mahdollisuus "p" voittaa peli juoksun aikana vedonlyönnissä, mikä on hänen mahdollisuus voittaa erä?
Ymmärtääkseni tenniksen säännöt erän voittaja on se, joka voittaa ensimmäisenä kuusi peliä, ja vähintään kahden pelin erolla. 6-6-tasapeli johtaa vain yhteen tie-break-peliin. Seuraava taulukko näyttää erän voittamisen todennäköisyyden, kun otetaan huomioon pelin voittamisen todennäköisyys.
Todennäköisyydet tenniksessä
| Todennäköisyys Pelivoitto | Todennäköisyys Erävoitto |
| 0,05 | 0,000003 |
| 0,1 | 0.000189 |
| 0,15 | 0,001899 |
| 0,2 | 0,009117 |
| 0,25 | 0,028853 |
| 0,3 | 0,06958 |
| 0,35 | 0.138203 |
| 0,4 | 0,23687 |
| 0,45 | 0,361085 |
| 0,5 | 0,5 |
| 0,55 | 0.638915 |
| 0,6 | 0,76313 |
| 0,65 | 0,861797 |
| 0,7 | 0,93042 |
| 0,75 | 0,971147 |
| 0,8 | 0,990883 |
| 0,85 | 0.998101 |
| 0,9 | 0.999811 |
| 0,95 | 0,999997 |
Kaava minkä tahansa pelin voittotodennäköisyyden p ja häviämisen q laskemiseksi on 1*p 6 + 6*p 6 *q + 21*p 6 *q 2 + 56*p 6 *q 3 + 126*p 6 *q 4 + 252*p 7 *q 5 + 504*p 7 *q 6
Olet veneessä, jossa on kivi, makealla järvellä. Heität kiven järveen. Nouseeko, laskeeko vai pysyykö vedenpinta samana suhteessa maahan (rantaan)? Työtoverini ajattelevat, että vedenpinta pysyy samana.
Vedenpinta rantaan nähden laskee. Veneen sisällä kivi painaa kanoottia ja työntää siten ympärillään olevaa vettä ylös. Syrjäytyneen veden määrä on yhtä suuri kuin kiven paino. Esimerkiksi 4,5 kilon kivi syrjäyttää 4,5 kiloa vettä ylöspäin. Kun kivi heitetään yli laidan, painolla ei ole merkitystä, vaan pikemminkin kiven tilavuudella. Joten kivi työntää ylöspäin kiven tilavuuden mukaisen vesimäärän. Kiven massa on suurempi kuin veden massa, joten kivi syrjäyttää enemmän sitä vasten painavaa vettä kuin siinä olevaa vettä. Järven pinta on siis korkeammalla, kun kivi on kanootissa, kuin pohjassa.
Miten tämä toimii?
- Ota laskin. (Et pysty tekemään tätä päässäsi.)
- Näppäile puhelinnumerosi kolme ensimmäistä numeroa (EI SUUNTANUMEROA)
- Kerro 80:llä
- Lisää 1
- Kerro 250:llä
- Lisää puhelinnumerosi neljä viimeistä numeroa
- Lisää puhelinnumerosi neljä viimeistä numeroa uudelleen.
- Vähennä 250
- Jaa luku kahdella
Tunnistatko vastauksen?
Kutsutaan puhelinnumerosi kolmea ensimmäistä numeroa x:ksi ja neljää viimeistä y:ksi. Katsotaanpa nyt, mitä minulla on kussakin vaiheessa.
- Valmis!
- X
- 80x
- 80x+1
- 250 * (80 x + 1) = 20 000 x + 250
- 20000x+250+y
- 20000x+250+2v
- 20000 x + 250 + 2 v - 250 = 20000 x + 2 v
- (20000x+2y)/2 = 10000x+y
Joten se on tietenkin sama kuin puhelinnumerosi. Tarvitsemme luvun 10000x siirtääksemme etuliitteen neljä paikkaa vasemmalle ja sitten lisäämme neljä viimeistä numeroa.
Arvontaan osallistutaan 27 000 dollarin arvoisesta autosta, ja lippuja myydään kuusi kappaletta hintaan 500,00 dollaria tai yksi kappale hintaan 100,00 dollaria. 68 lippua on myyty, ja huomenna on ostopäivä. Tiedän, että 50 %:n voittotodennäköisyydellä minun on käytettävä 5 666,44 dollaria ja 66,66 %:n voittotodennäköisyydellä 11 332,88 dollaria (eikö niin?). Kuinka paljon minun pitäisi käyttää (tai kuinka monta lippua minun on ostettava) varmistaakseni käytännössä, että "voitan" auton? (90 %? 95 %?) Onko tämä arvonta pelaamisen arvoinen, vai pitääkö minun käyttää auton hinta?
Olet oikeassa 1/2- ja 2/3-todennäköisyyksien suhteen. Jos ostat t lippua, voittotodennäköisyytesi on t/(68+t). Joten 90 %:n todennäköisyydellä ratkaise t seuraavasti.
0,9 = t/(68 + t)
0,9 * (68 + t) = t
61,2 = 0,1 t
t = 612 eli 51 000 dollaria
95 prosentille...
0,95 = t/(68 + t)
0,95(68 + t) = t
64,6 = 0,05 t
t = 1292 eli 107 666,67 dollaria
Olettaen, että auto on sinulle arvoltaan 27 000 dollaria, sinun kannattaa lopettaa lippujen ostaminen heti, kun seuraava myyty lippu ei lisää voittotodennäköisyyttäsi tarpeeksi oikeuttaakseen hinnan.
Jotta lippu olisi hintansa arvoinen, sen pitäisi lisätä voittotodennäköisyyttäsi p:llä, missä...
27000*p=(500/6)
p=0,003086
Oletetaan, että t on ostamiesi lippujen lukumäärä, joilla et halua ostaa vielä yhtä lippua.
[(t+1)/(t+68+1)] − [t/(t+68)] = 0,003086
[(t+1)/(t+69)] − [t/(t+68)] = 0,003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0,003086
[(( t² + 69t+68)/((t+69)*(t+68))] − [( t² + 69t)/((t+68)*(t+69))] = 0,003086
68/((t+68)*(t+69)) = 0,003086
((t+68)*(t+69)) = 220,32
t² + 137t+4692 = 22032
t2 +137t - 17340=0
t=(-137+/-(137 2 -4*1*-17340) 2 )/2
t = 79,9326
Testataan tätä syöttämällä joitakin arvoja ostetuille lipuille olettaen, että pelaaja voi aina ostaa lippuja hintaan 500 dollaria / 6 = 83,33 dollaria kappale.
79 lipulla kustannuksesi on 79 * (500 / 6) = 6 583,33 dollaria, voittotodennäköisyytesi on 79 / (79 + 68) = 53,74 %, odotettu tuotto on 27 000 dollaria * 0,5374 = 14 510,20 dollaria ja odotettu voitto on 14 510,20 dollaria - 6 583,33 dollaria = 7 926,87 dollaria.
80 lipulla kustannuksesi on 80 * (500 / 6) = 6 666,67 dollaria, voittotodennäköisyytesi on 80 / (80 + 68) = 54,04 %, odotettu tuotto on 27 000 dollaria * 0,5405 = 14 594,59 dollaria ja odotettu voitto on 14 594,59 dollaria - 6 666,67 dollaria = 7 927,92 dollaria.
81 lipulla kustannuksesi on 81 * (500 / 6) = 6 750,00 dollaria, voittotodennäköisyytesi on 81 / (81 + 68) = 54,36 %, odotettu tuotto on 27 000 dollaria * 0,5436 = 14 677,85 dollaria ja odotettu voitto on 14 594,59 dollaria - 6 750,00 dollaria = 7 927,85 dollaria.
Voimme siis nähdä, että odotettu maksimivoitto on korkeimmillaan 80 lippua.
Yritän vertailla vanhan jääkaapin vaihtamisen kustannuksia nyt sähkökustannusten säästämiseksi verrattuna siihen, että odotan jääkaapin hajoamista ennen sen vaihtamista. Voin laskea, kuinka paljon halvempaa uuden jääkaapin käyttö on vanhaan verrattuna: 37 dollaria vuodessa, se on helppoa. Mutta miten voin ottaa huomioon uuden jääkaapin kustannukset? Sanotaan, että uusi jääkaappi maksaa 425 dollaria. En voi sanoa, että *kaikki* tuo 425 dollaria on uusi kulu, koska minun on vaihdettava vanha jääkaappi *jonain päivänä*, ellei nyt, joten minulla on se uuden jääkaapin kulu joka tapauksessa jossain vaiheessa. Oletetaan, että tyypillinen jääkaappi kestää 14 vuotta ja vanha jääkaappini on 9 vuotta vanha, joten jos vaihtaisin sen nyt, vaihtaisin sen 5 vuoden kuluttua. Yritin tehdä kaksisarakkeisen taulukon, jossa vertailen nykyisen jääkaapin 9 vuoden ylläpito- ja vaihtamiskustannuksia nykyiseen vaihtamiseen verrattuna, mutta en tiennyt, miten tehdä suora vertailu, koska en tiennyt kuinka pitkälle tulevaisuuteen kustannuksia pitäisi ottaa huomioon, ja koska jääkaapit vaihdetaan eri vuosina. Miten vertaan vaihtamisen taloudellisuutta nyt verrattuna myöhempään? Muuten, tämä ei koske omaa tilannettani, koska nykyinen jääkaappini on luultavasti 30 vuotta vanha. Tämä on, öö, ystävää varten.
Jos pidät nykyisen jääkaapin, viiden vuoden kuluttua olet käyttänyt sähköön 37 * 5 = 185 dollaria enemmän kuin uuteen. Jos vaihdat sen nyt, menetät 425 dollaria, mutta olettaen lineaarisen poiston viiden vuoden kuluttua, se on silti arvoltaan 425 dollaria * (9/14) = 273,21 dollaria. Joten olet menettänyt 425 dollaria * (5/14) = 151,79 dollaria poistojen vuoksi. Joten uuden jääkaapin poistokustannukset ovat pienemmät kuin vanhan säilyttämisestä aiheutuvat lisäsähkökustannukset, joten kannatan uuden ostamista nyt.
Jos ihmisiä on kolme, niin mikä on todennäköisyys, että ainakin kahdella heistä on syntymäpäivä samana päivänä?
Jos karkauspäivää ei oteta huomioon, kaikkien kolmen eri syntymäpäivän todennäköisyys on (364/365)*(363/365) = 0,99179583. Joten ainakin yhden yhteisen syntymäpäivän todennäköisyys on 1 - 0,99179583 = 0,00820417.
Huoneessa on viisi henkilöä. Mikä on todennäköisyys, että vähintään kaksi heistä on syntynyt samana syntymäkuukautena?
Yksinkertaisuuden vuoksi oletetaan, että jokaisella henkilöllä on 1/12 todennäköisyys syntyä kunakin kuukautena. Todennäköisyys sille, että kaikki viisi henkilöä syntyvät eri kuukausina, on (11/12)*(10/12)*(9/12)*(8/12) = 0,381944. Joten saman kuukauden todennäköisyys on 1 - 0,381944 = 0,618056.
Meille on annettu töissä haaste – ihan vain huvin vuoksi, eikä kukaan meistä osaa ratkaista sitä. Maanviljelijällä on viisi perävaunullista lampaita. Neljässä perävaunussa on 39 kg painavia lampaita ja viidennessä perävaunussa 40 kg painavia lampaita. Kaikki lampaat ovat samanlaisia. Hän menee markkinoille. Hän haluaa selvittää, missä perävaunuissa on 40 kg painavat lampaat, ja hän saa käyttää isoa vaakaa vain kerran!!! Miten hän tekee sen? Auttakaa, tämä ajaa meidät kaikki hulluiksi työpaikallani – se on eläinlääkäri!!
Vastaus on kolumnin lopussa.
Vastaus lampaan kysymykseen
Ota yksi lammas perävaunusta 1, kaksi perävaunusta 2, kolme perävaunusta 3, neljä perävaunusta 4 ja nolla perävaunusta 5. Jos kaikki lampaat painaisivat 39 kg, kokonaispaino olisi 39 * 10 = 390 kg. Kuitenkin 0–4 lammasta on yhden kg painavampia. Jos kokonaispaino on 391, vaa'alla on yksi painava lammas; sen on täytynyt tulla perävaunusta 1. Samoin, jos kokonaispaino on 392, vaa'alla on kaksi painavaa lammasta, joiden on täytynyt tulla perävaunusta 2. Samalla tavalla painoarvo 393 tarkoittaa, että painavat lampaat ovat perävaunussa 3, painoarvo 394 tarkoittaa, että painavat lampaat ovat perävaunussa 4 ja painoarvo 390 tarkoittaa, että painavat lampaat ovat perävaunussa 5.
Mitkä ovat todennäköisyydet sille, että istun samalla lennolla lentävän hyvännäköisen tytön vieressä 180-paikkaisessa lentokoneessa?
Se riippuu ryhmän istumapaikkojen lukumäärästä. Useimmilla kotimaanlennoilla on kolme paikkaa käytävän kummallakin puolella. Tämä tekisi 60 kolmen istumapaikan ryhmää. Kun ensimmäinen teistä on istuutunut, samassa ryhmässä on kaksi paikkaa jäljellä olevista 179:stä, joten todennäköisyys olla samassa ryhmässä on 2/179 = 1,12 %. Tällöin et voi saada ketään muuta keskimmäiselle paikalle. Todennäköisyys sille, että kolmas henkilö on keskimmäisellä paikalla, on 1/3. Joten vastaus on (2/179) * (2/3) = 0,74 % eli 1/134,25.
Kolme loogikkoa pelaa peliä. Jokaisen on salaa kirjoitettava muistiin positiivinen kokonaisluku. Loogikko, jolla on pienin ainutlaatuinen kokonaisluku, voittaa 3 dollaria. Jos kaikilla kolmella on sama luku, kukin voittaa 1 dollarin. Loogikot ovat itsekkäitä ja kukin haluaa maksimoida omat voittonsa. Kommunikointi ei ole sallittua. Mitä strategiaa kukin loogikko noudattaa?
Vastaus näkyy seuraavassa sarakkeessa.
Normaalisti sanoisin, että tämä on minun alueeni ulkopuolella. Työskenneltyäni kuitenkin kahdeksan vuotta entisenä valtion aktuaarina tiedän veroista pari asiaa. Lukemani perusteella suurin osa Warren Buffetin tuloista määritellään myyntivoitoiksi, joita verotetaan vain 15 prosentin verokannalla. Tykkäsit tai et, verolait sallivat sen. Minua hämmensi se, miksi hänen sihteerinsä maksoi jopa 30 prosenttia. Tämän videon mukaan hän laski mukaan "palkka- ja tuloverot". "Palkkaveroilla" hän ilmeisesti tarkoitti sosiaaliturva- ja sairausvakuutusveroja. Katsotaanpa, onko 30 % kohtuullinen liittovaltion veroprosentti hänen sihteerilleen.
Vuonna 2007 ylintä veroluokkaa verotettiin 35 %:lla, mutta se koskee vain yli 349 700 dollarin tuloja. Siihen asti tuloja verotetaan paljon vähemmän. Oletetaan, että hänen sihteerinsä on naimaton, hänellä ei ole huollettavia lapsia, ja hänen palkkansa oli 100 000 dollaria. Vähennetään ensin vähimmäisvähennykset. Vuonna 2007 naimattomien veroilmoittajien vakiovähennys oli 5 350 dollaria. Henkilökohtainen vähennys oli 3 400 dollaria. Jäljelle jää siis 100 000 dollaria - 5 350 dollaria - 3 400 dollaria = 91 250 dollaria tuloveroa. Vuonna 2007 naimattomien veroilmoittajien verokanta oli 10 % ensimmäisistä 7 825 dollarin tuloista, sitten 15 % 31 850 dollariin asti, sitten 25 % 77 100 dollariin asti ja 28 % 160 850 dollariin asti. Joten hänen tuloveronsa olisi ollut =0,1 × 7 825 $ + 0,15 × (31 850 $ - 7 825 $) + 0,25 × (77 100 $ - 31 850 $) + 0,28 × (91 250 $ - 77 100 $) = 19 660,75 $. Se on vain 19,7 % hänen tuloistaan. Kaikki oletukseni, kuten hänen tulonsa, veroilmoituksen tila ja erittelyn puute, toimivat häntä vastaan tai korkeamman verokannan puolesta.
Tarkastellaanpa nyt sosiaaliturvaa ja Medicarea. Vuonna 2007 sosiaaliturvavero oli 6,2 %, ja sen jälkeen se lakkaa kokonaan olemasta 97 500 dollarin tuloihin asti. Vuoden 2007 Medicare-verokanta oli 1,45 % ilman ylärajaa. Joten hänen yhteenlaskettu sosiaaliturva- ja Medicare-veronsa olisi ollut 6,2 % * 97 500 + 1,45 % * 100 000 = 7 495 dollaria. Nämä verot laskemalla hänen kokonaisverokantansa olisi ollut (19 660,75 dollaria + 7 495 dollaria) / 100 000 dollaria = 27,2 %. Silti jäämme 2,8 % 30 prosentista.
Paras arvaukseni on, että hän ottaa myös huomioon sen, että viime kädessä hän maksaa työnantajan vastaavat sosiaaliturva- ja sairausvakuutusverot. Niille, jotka eivät tiedä, sosiaaliturva- ja sairausvakuutusverot ovat itse asiassa kaksinkertaiset työtoveroistasi vähennettyyn verrattuna. Työnantaja maksaa toisen puoliskon. Jotkut, myös minä, kuitenkin väittävät, että viime kädessä työntekijä maksaa molemmat. Jos työnantajan ei tarvitsisi maksaa kyseisiä veroja, hänellä olisi enemmän rahaa maksaa työntekijöilleen. On helppo tuntea niin, kun on itsenäinen ammatinharjoittaja, kuten minä, ja joutuu maksamaan molemmat osuudet. Jos sosiaaliturva-/sairausvakuutusvero kaksinkertaistetaan, verokanta on nyt (19 660,75 dollaria + 2 × 7 495 dollaria) / 100 000 dollaria = 34,7 %. Oletan, että 4,7 %:n ero johtuu siitä, että hän ansaitsee alle 100 000 dollaria, on naimisissa, hänellä on huollettavia, hän erittelee vähennykset tai jotain näiden yhdistelmää.
Sosiaaliturva- ja Medicare-verot eivät vaikuttaisi juurikaan Warren Buffetiin. Ensinnäkin 97 500 dollarin sosiaaliturvamaksukatto olisi hänelle merkityksetön. Toiseksi nämä verot koskevat palkkoja, eivät pääomatuloja, kuten hän määrittelee suurimman osan tuloistaan.
Joten, se on paras arvaukseni herra Buffetin lausunnon taustalla olevista laskelmista.
Päivitys: Pian tämän kolumnin ilmestymisen jälkeen sain seuraavan vastauksen. Oikeudenmukaisuuden nimissä esitän seuraavan argumentin, jonka mukaan herra Buffet maksaa liikaa veroja.
Luin mielenkiinnolla vastauksesi "raivoilleen" osoitetulle henkilölle, joka pitää epäreiluna sitä, että Warren Buffet maksaa veroja vähemmän kuin hänen sihteerinsä. Olin pettynyt vastaukseesi, joka ei korjaa väärää tietoa, jonka mukaan herra Buffet maksaisi vähemmän veroja kuin hänen sihteerinsä.Ensinnäkin, kuten totesit, sijoitustuloja verotetaan 15 %:n verokannalla. Tämä on käytännössä kaksinkertainen verotus, koska herra Buffetin sijoittamat ansiotulot verotettiin hänen 36 %:n marginaaliverokannan mukaisesti. Omenoiden ja appelsiinien vertailu (työtulo vs. sijoitustulo).
Toiseksi, ei pitäisi katsoa prosenttiosuutta. Uhkapelien termein pitäisi katsoa sen sijaan "voittosummaa". Olen hyvin varma, että herra Buffet maksoi miljoonia dollareita veroja samana vuonna, jona hänen sihteerinsä maksoi tuhansia dollareita.Eikö lukijan pitäisi olla enemmän raivoissaan siitä, että yksi maan kansalainen maksaa tuhansia kertoja enemmän kuin muut kansalaiset samoista julkisista palveluista? Hän voisi yhtä hyvin sanoa kerran: "Kuulin, että Warren Buffet maksoi miljoona kertaa enemmän veroja kuin hänen sihteerinsä, se on pöyristyttävää!"
Ajattelin vain huomauttaa, että pelkän "prosenttiosuuden" katsominen "todellisen voiton" sijaan on virhepäätelmä. Samanlainen kuin monet uhkapelivirheesi .
Ystävällisin terveisin,
Kevin A. (Dallas)
Kiitos viihdyttävästä matematiikkapulmakokoelmastasi. Tyttöystäväni ja minä kehitimme tämän muunnelman merirosvopulmasta. Entä jos kaikki merirosvot ovat samanarvoisia ja jokaisella kierroksella jakolaskun ehdottaja valitaan arvalla? Tässä muunnelmassa oletetaan, että jokaisen merirosvon tärkein prioriteetti on maksimoida odotettu vastaanottamiensa kolikoiden määrä. Minulla on mielestäni ratkaisu, mutta ehkä haluaisit kokeilla sitä ensin. Kiitos vielä kerran.
Ole hyvä. Jos jäljellä on vain kaksi merirosvoa, ehdotuksen tekijällä ei ole toivoa, koska toinen merirosvo äänestää ei. Arvottu saa nollan ja toinen kaikki 1000. Joten ennen arvontaa odotusarvo kahden merirosvon ollessa jäljellä on 500 kolikkoa.
Kolmen merirosvon vaiheessa arvotun merirosvon tulisi ehdottaa, että hän antaisi itselleen toiselle merirosvolle luvut 501 ja 499. Se, joka saa luvun 501, äänestää kyllä, koska se on enemmän kuin odotettu arvo 500 äänestämällä ei. Ennen arvontaa, kun jäljellä on kolme merirosvoa, sinulla on 1/3 mahdollisuus saada 0, 499 tai 501 kolikkoa, keskimäärin 333,33.
Neljän merirosvon vaiheessa arvotun merirosvon tulisi antaa 334 kahdelle muulle merirosvolle ja 332 itselleen. Näin hän saa kaksi kyllä-ääntä merirosvoilta, jotka saavat 334 kolikkoa, koska he haluaisivat mieluummin 334 kuin 333,33. Oma äänesi mukaan lukien sinulla on 3 ääntä neljästä. Ennen arvontaa kunkin merirosvon odotusarvo on keskiarvo 0:sta, 334:stä, 334:stä ja 332:sta eli 1000/4=250.
Samalla logiikan mukaisesti viiden merirosvon tasolla nostetun merirosvon tulisi antaa 251 mille tahansa kahdelle merirosvolle ja 498 itselleen. Toisin kuin alkuperäisessä tehtävässä, ei ole tarpeen työskennellä taaksepäin. Jaa vain kolikoiden lukumäärä merirosvojen lukumäärällä, itseäsi lukuun ottamatta. Anna sitten puolet heistä (pyöristämällä alaspäin) keskiarvosta ja yksi kolikko lisää.
Tarvitsen apua Eternity II -nimisen pulman kanssa. Palkintona pulman ratkaisemisesta on huikeat 2 000 000 dollaria, mikä on minulle huomattava summa rahaa. Tässä on linkki haastatteluun, jossa on mukana pelintekijä itse Christopher Monckton (monen muun muassa Margaret Thatcherin entinen neuvonantaja). Peli ei tietenkään oikeastaan ole uhkapelaamista, mutta tästä huolimatta voisit ehkä lisätä verkkosivullesi sanan tai pari siitä.
Pelintekijä kerskuu yllä olevassa linkissä pulman ratkaisemattomuudella. Alan epäillä, että hän on itse asiassa oikeassa ja että hän itse on ainoa, joka lopulta rikastuu myymällä tuota (naurettavaa mutta kiehtovaa) peliä. Miten sinä, matemaatikko ja kaikki muu, ratkaisisit tällaisen pulman?
Toivottavasti olet tyytyväinen; olen ollut tämän palapelin lumoissa viimeisen kuukauden tai pari. Olin onnekas (tai ehkä epäonninen) löytäessäni 256-palaisen palapelin paikallisesta Borders-kirjakaupasta, mutta minun piti ostaa neljä vihjepalapeliä eBaysta joltain australialaiselta kaverilta.
Kirjoitin ohjelman, joka ratkaisee helposti neljä vihjepulmaa. Se ratkaisi 72-palaisen vihjepulman nro 4 alle sekunnissa. Tein sen yksinkertaisella raa'an voiman rekursiivisella ohjelmalla. Piirsin pelilaudalle polun alkaen reunasta. Jokaisessa kohdassa ohjelma kävi läpi kaikki käyttämättömät palat etsien sopivaa. Jos se löysi sellaisen, se siirtyi seuraavaan ruutuun; jos ei löytänyt, se siirtyi yhden ruudun taaksepäin.
Kaksi tietokonetta on paininut 256-palaisen kahden miljoonan dollarin palapelin parissa viikkojen ajan, eikä kumpikaan ole päässyt lähellekään. Olen samaa mieltä siitä, mitä luoja sanoi tuossa videossa: vaikka kymmenen miljoonaa maailman nopeinta tietokonetta kytkettäisiin päälle, ne eivät välttämättä vieläkään löytäisi ratkaisua maailmankaikkeuden kuolemaan mennessä. Luulisi, että olisin kuunnellut hänen varoitustaan ennen aloittamista, mutta hyvän palapelin edessä kaikki käytännöllinen ajatus ajankäytöstä menee romukoppaan.
Minulla on paljon ideoita oikotekepeistä, mutta vaikka ne nopeuttaisivat ohjelmaani miljardikertaisesti, ne eivät luultavasti silti auttaisi. Olen erittäin vaikuttunut, jos joku ratkaisee tämän. Minua todella vaivaa se, että mielestäni on olemassa jokin löytämätön matematiikan haara, joka voisi ratkaista tällaiset pulmat helposti. Siihen asti uskon, että ylistetty yritys ja erehdys ovat paras tapa ratkaista se. Nykyajan tietokoneet ovat yksinkertaisesti liian hitaita ja yhdistelmien määrä liian suuri, jotta sillä olisi paljonkaan mahdollisuuksia onnistua.

Oletetaan, että kahden kaupungin välinen etäisyys on 1600 kilometriä. Ilman tyyneyttä lentokone voi matkustaa 800 km/h nopeudella. Kestääkö edestakainen lento kauemmin ilman tuulta tai jos myötätuuli puhaltaa suoraan 160 km/h toiseen suuntaan ja vastatuuli on yhtä suuri toiseen suuntaan?
Tuulen ollessa tyyni lento kestää kaksi tuntia suuntaansa, yhteensä neljä tuntia. Myötätuulessa kone matkustaa 967 km/h, joten matkan kesto on 1000/1000 = 1,667 tuntia. Vastatuulessa kone matkustaa 640 km/h, joten matkan kesto on 1000/400 = 2,5 tuntia. Tuulessa kokonaisaika on siis 4,167 tuntia eli 10 minuuttia pidempi.
Tämä vain osoittaa, että keskiarvojen laskeminen on vaarallista. Et voi sanoa matkan keskinopeudeksi 800 km/h, jos se on 640 km/h yhteen suuntaan ja 960 km/h toiseen, koska 640 km/h osuus on pidemmän ajanjakson aikana.
Jos tämä ei ole intuitiivista, harkitse 800 km/h tuulta. Koneella kestäisi tunnin pelkän tuulen kanssa, mutta se pysyisi paikallaan toisinpäin, mikä kestäisi ikuisuuden.
Osallistuin hiljattain arvontaan, jossa oli 7 033 palkintoa ja heidän mukaansa voiton todennäköisyys on 1/13. Ostin 5 lippua. Mitkä ovat todelliset todennäköisyyteni voittaa jotain? Lisäksi on 40 suurta palkintoa. Mitkä ovat todennäköisyyteni voittaa suuri palkinto?
Yksinkertaisuuden vuoksi jätetään huomiotta se tosiasia, että mitä enemmän lippuja ostat, sitä alhaisemmaksi kunkin lipun arvo muuttuu, koska kilpailet itseäsi vastaan. Kaikkien viiden lipun häviämisen todennäköisyys on kuitenkin (12/13) 5 = 67,02 %. Joten ainakin yhden palkinnon voittamisen todennäköisyys on 32,98 %. Rummussa on yhteensä 7033 × 13 = 91 429 lippua ennen kuin ostat yhtään. 91 429 - 40 = 91 389 eivät ole suuria palkintoja. Todennäköisyys sille, ettei viidellä lipulla voita suuria palkintoja, on (91 389/91 429) 5 = 99,78 %. Joten ainakin yhden suuren palkinnon voittamisen todennäköisyys on 0,22 % eli 1/458.
Olen yrittänyt ratkaista pulmaa muutaman kuukauden ajan, ilman minkäänlaista edistystä. Jos aika sallii, toivon, että voitte antaa minulle anteeksi, sillä se on pitänyt minut hereillä öisin :-). Joka tapauksessa, sanastossa "Beyond Counting -- Exhibit CAA" on kolme numero- ja kirjainsarjaa, jotka muodostavat sanastomerkinnän "Magic Numbers" -haulle. Yksi näistä numeroista on jopa kirjan kantta, joten oletan niiden olevan jonkin verran tärkeitä. Onko sinulla ajatuksia?
En sano tätä usein, mutta minulla ei ole aavistustakaan. Kuten totesit toisessa sähköpostissa, he käyttävät Yhdysvaltain dollarin sarjanumeron muotoa, kaksi kirjainta ja niiden välissä kymmennumeroinen luku. Tekijänoikeuksien kunnioittamiseksi en kerro tässä, mitä numerot ovat.
Olen utelias tietämään, mitä sille Eternity II -pulmahaasteelle tapahtui. Ratkaistiinko se? Työstätkö sitä vielä?
Kiitos kysymyksestä. En ole koskenut siihen sitten 17. marraskuuta 2008 julkaistun Kysy velholta -kolumnin . Heidän verkkosivujensa mukaan heillä on "tarkastuspäivät" 31. joulukuuta 2009 ja tarvittaessa 2010. Mielestäni sitä ei koskaan ratkaista.
Päivitys: Eternity II -verkkokokoa ei näytä enää olevan olemassa.
Luin kiehtovana Wizard'sin blogia Arnold Schwarzeneggerin veto-kirjeestä. Kysymykseni liittyy kuvernöörin naurettavaan mutta ennustettavaan vastaukseen. Kuvernööri totesi, että se oli vain "villi sattuma". Huolimatta ylivoimaisista aihetodisteista (lakiesityksen laatija ja kirjeen vastaanottaja oli henkilö, joka oli loukannut kuvernööriä viikkoa aiemmin), onko sinulla arviota siitä, mikä on todennäköisyys sille, että täsmälleen seitsemän rivin pituinen kirjain kirjoittaa tämän lauseen sattumalta? Mielestäni käytettyjen kirjainten perusteella se on vielä epätodennäköisempää kuin vain antaa 1/26 mahdollisuus kullekin. Ei näytä siltä, että U, Y ja erityisesti K olisivat yleisiä sanojen alkukirjaimia.
Jos loukkaannut helposti, siirry seuraavaan kysymykseen.
Niiden lukijoideni tiedoksi, jotka eivät lukeneet kyseistä blogia, katsokaa Kalifornian kuvernöörin Arnold Schwarzeneggerin muistion (PDF) jokaisen rivin ensimmäistä kirjainta alkaen F-kirjaimella alkavasta rivistä.
Tätä käsiteltiin kumppanisivustollani Wizard of Vegas . Löysin vastauksen etsimällä englannin kielen ensimmäisen sanan jokaisen kirjaimen esiintymistiheyden Wikipediasta .
Sanafrekvenssi ensimmäisen kirjaimen mukaan
| Kirje | Taajuus |
| A | 11,60 % |
| B | 4,70 % |
| C | 3,51 % |
| D | 2,67 % |
| E | 2,00 % |
| F | 3,78 % |
| G | 1,95 % |
| H | 7,23 % |
| Minä | 6,29 % |
| J | 0,63 % |
| K | 0,69 % |
| L | 2,71 % |
| M | 4,37 % |
| N | 2,37 % |
| O | 6,26 % |
| P | 2,55 % |
| Q | 0,17 % |
| R | 1,65 % |
| S | 7,76 % |
| T | 16,67 % |
| U | 1,49 % |
| V | 0,62 % |
| Länsi | 6,66 % |
| X | 0,01 % |
| Y | 1,62 % |
| Z | 0,05 % |
Todennäköisyyden arvioiminen sille, että Arnoldin viesti oli todellakin vain sattumaa, olisi Prob(F) × Prob(U) × ... × prob(U) = 0,0378 × 0,0149 × 0,0351 × 0,0069 × 0,0162 × 0,0626 × 0,0149 = 1/486 804 391 348. Tämä ei edes ota huomioon sitä tosiasiaa, että rivinvaihto oli kätevästi kahden sanan välisen välilyönnin paikalla.
Haluan kiittää Eliot J.:tä ja Jonathan F.:ää heidän panoksestaan tähän ratkaisuun.
Lentokentän matkatavarahihnalla mitä enemmän laukkuja minulla on noudettavana, sitä kauemmin joudun odottamaan kaikkien laukkujen saapumista. Jos otan vain yhden laukun, joudun odottamaan, kunnes noin puolet laukkuista tulee ulos. Jos otan kaksi laukkua, odotukseni on pidempi, ja jos otan kolme, vielä pidempi. Olettaen, että laukkuni sekoittuvat satunnaisesti muiden joukkoon, mikä on yleinen kaava laukkujen lukumäärälle, joka minun on odotettava ennen kuin pääsen noutamaan kaikki laukkuni, suhteessa laukkujeni lukumäärään ja laukkujen kokonaismäärään?
Määritellään ensin joitakin muuttujia seuraavasti:
n = laukkujesi lukumäärä
b = pussien kokonaismäärä
Kun laukkujen kokonaismäärä kasvaa, vastaus lähestyy arvoa b×n/(n+1). Suurelle lentokoneelle tämä antaa hyvän arvion. Jos kuitenkin haluat olla tarkka, vastaus on
[b× combin (b,n)-(summa, kun i=n arvoon b-1 joukosta combin(i,n))]/combin(b,n)
Jos esimerkiksi matkalaukkuja on yhteensä 10 ja neljä niistä on sinun, odotettu odotusaika =
[10×yhdistelmä(10,4)-yhdistelmä(4,4)-yhdistelmä(5,4)-yhdistelmä(6,4)-yhdistelmä(7,4)-yhdistelmä(8,4)-yhdistelmä(9,4)]/yhdistelmä(10,4) = 8,8 pussia.
Ratkaisu:
Tapojen lukumäärä n pussin poimimiseksi b pussista on combin(b,n). Todennäköisyys sille, että kaikki pussisi tulevat ulos ensimmäisten x pussin joukosta, on combin(x,n)/combin(b,n). Todennäköisyys sille, että viimeinen pussisi on x :s ulos tuleva pussi, on (combin(x,n)-combin(x-1,n))/combin(b,n), kun x > = n + 1. Kun x = n, se on 1/combin(b,n).
Joten odotetun odotusajan suhde kokonaisodotusaikaan on:
n×combin(n,n)/combin(b,n) +
(n+1)×(yhdistää(n+1,n)-yhdistää(n,n))/yhdistää(b,n) +
(n+2)×(yhdistää(n+2,n)-yhdistää(n+1,n))/yhdistää(b,n) +
.
.
.
+
(b-1)×(yhdiste(b-1,n)-yhdistää(b-2,n))/yhdistää(b,n) +
b×(yhdistää(b,n)-yhdistää(b-1,n))/yhdistää(b,n)
Teleskooppisumman avulla tämä voidaan yksinkertaistaa muotoon:
[b × yhdistä (b, n) - yhdistä (b-1, n) - yhdistä (b - 2, n) -... - yhdistä (n, n)] / yhdistä (b, n)
Eräs lukija kirjoitti myöhemmin, että vastaus voidaan sieventää muotoon n×(b+1)/(n+1). Tämä voidaan osoittaa induktiolla, joka on pätevä menetelmä, mutta se jättää minut aina emotionaalisesti tyytymättömäksi.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Myyn veistoksia. Keskimäärin seitsemästä myydystä veistoksesta yksi on kilpikonna ja loput ovat muuntyyppisiä veistoksia. Kuinka monta kilpikonnaa minulla täytyy olla varastossa, jos haluan 90 %:n todennäköisyyden sille, etteivät ne lopu seuraavien 100 myydyn veistoksen aikana?

Olkoon t valmistettujen kilpikonnien lukumäärä ja x myytyjen kilpikonnien lukumäärä.
pr(x<=t)=0.9
pr(x-14,29<=t-14,29)=0,9
pr((x-14,29)/3,5)<=(t-14,29)/3,5))=0,9
Epäyhtälön vasen puoli noudattaa standardinormaalijakaumaa (keskiarvo 0, keskihajonta 1). Seuraavassa vaiheessa hyväksytään johdantotilastokurssi tai jonkinlainen uskomus.
(t-14,29)/3,5 = normsinv(0,9) Tämä on Excel-funktio.
(t - 14,29) / 3,5 = 1,282
t-14,29 = 4,4870
t = 18,77
Kukaan ei todennäköisesti osta 0,77 kilpikonnapatsasta, joten pyöristäisin ylöspäin 19:ään. Binomijakauman mukaan todennäköisyys myydä 18 tai vähemmän on 88,35 % ja 19 tai vähemmän on 92,74 %. Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegas foorumilla.
Viisi merimiestä selviää haaksirikosta. Ensimmäiseksi he keräävät kookospähkinöitä ja laittavat ne suureen yhteiseen kasaan. Heidän oli tarkoitus jakaa ne tasan jälkeenpäin, mutta kovan kookospähkinöiden keräämisen jälkeen he ovat liian väsyneitä. Niinpä he menevät nukkumaan yöksi aikomuksenaan jakaa kasa aamulla.
Merimiehet eivät kuitenkaan luota toisiinsa. Keskiyöllä yksi heistä herää ottamaan oman osuutensa. Hän jakaa kasan viiteen yhtä suureen osaan ja jättää yhden kookospähkinän jäljelle. Hän hautaa osuutensa maahan, yhdistää neljä muuta kasaa uudeksi yhteiseksi kasaksi ja antaa jäljellä olevan kookospähkinän apinalle.
Kello 1.00, 2.00, 3.00 ja 4.00 kaikki neljä muuta purjehtijaa tekevät täsmälleen saman asian.
Aamulla kukaan ei tunnusta tekoaan, ja he jatkavat alkuperäisen suunnitelman mukaisesti ja jakavat kasan tasan. Jälleen yksi kookospähkinä jää jäljelle, ja he antavat sen apinalle.
Mikä on pienin mahdollinen kookospähkinöiden lukumäärä alkuperäisessä kasassa?
"Selaa vastausta 100 riviä alaspäin.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Alkuperäisessä pinossa oli 15 621 kookospähkinää. Vieritä alaspäin vielä 100 riviä nähdäksesi ratkaisuni.
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
Olkoon c alkuperäisen pinon kookospähkinöiden lukumäärä ja f kunkin merimiehen lopullinen osuus viimeisen jaon jälkeen.
Kun merimies 1 ottaa osuutensa ja antaa apinalle kookospähkinänsä, jäljelle jää (4/5) × (c-1) = (4c-1) /5.
Kun merimies 2 ottaa osuutensa ja antaa apinalle kookospähkinänsä, jäljelle jää (4/5)×(((4c-1)/5)-1) = (16c-36)/25.
Kun merimies 3 ottaa osuutensa ja antaa apinalle kookospähkinänsä, jäljelle jää (4/5)×(((16c-36)/25)-1) = (64c-244)/125.
Kun merimies 4 ottaa osuutensa ja antaa apinalle kookospähkinänsä, jäljelle jää (4/5)×(((64c - 244)/125)-1) = (256c - 1476)/625.
Kun merimies 5 ottaa osuutensa ja antaa apinalle kookospähkinänsä, jäljelle jää (4/5)×(((256c - 1476)/625)-1) = (1024c - 8404)/3125.
Aamulla jokaisen merimiehen osuus jäljellä olevasta kasasta on f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 jäljellä.
Kysymys kuuluu siis, mikä on c:n pienin arvo, jolle f=(1024 × c - 11529) / 15625 on kokonaisluku. Ilmaistaan c f:n avulla.
(1024 × c⁻¹⁵) / 15625 = f
1024c - 11529 = 15625 × f
1024c = 15625f+11529
c = (15625f+11529)/1024
c = 11 + ((15625 × f + 265) / 1024)
c = 11 + 15 × f + (265 × (f + 1)) / 10²²
Mikä on siis pienin f, jolle 265×(f+1)/1024 on kokonaisluku? Luvuilla 265 ja 1024 ei ole yhteisiä tekijöitä, joten luvun f+1 on oltava jaollinen luvulla 1024. Pienin mahdollinen arvo luvulle f+1 on 1024, joten f=1023.
Näin ollen c = (15625 × 10²⁻² + 11529) / 10²⁻ = 15 621.
Tässä on kuinka monta kookospähkinää kukin henkilö ja apina saivat:
Kookospähkinäongelma
| Merimies | Kookospähkinät |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| Apina | 6 |
| Kokonais | 15621 |
David Filmer, joka haastoi minut kysymyksellä, tiesi jo vastauksen. Itse asiassa hän kysyi minulta kaavaa yleiselle s merimiehen tapaukselle, mutta minulla oli jo tarpeeksi vaikeuksia erityistapauksen kanssa, jossa oli 5 merimiestä. David huomauttaa, että yleisen tapauksen vastaus on c = s s+1 - s + 1.
Jätän tuon todistuksen lukijan tehtäväksi.
Tässä on linkkejä vaihtoehtoisiin ratkaisuihin ongelmaan:
Miehelle annetaan kaksi rahaa täynnä olevaa kirjekuorta. Toisessa kirjekuoressa on kaksi kertaa enemmän rahaa kuin toisessa. Kun mies on valinnut kirjekuorensa, avannut ja laskenut sen, hänelle annetaan mahdollisuus vaihtaa se toiseen kirjekuoreen. Kysymys kuuluu, hyötyykö mies kirjekuoren vaihtamisesta?
Vaikuttaisi siltä, että vaihtamalla miehellä olisi 50 %:n mahdollisuus kaksinkertaistaa rahansa, jos alkuperäinen kirjekuori on pienempi summa, ja 50 %:n mahdollisuus puolittaa se, jos alkuperäinen kirjekuori on suurempi summa. Olkoon siis x alkuperäisen kirjekuoren sisältämä summa ja y sen vaihtamisen arvo:
y = 0,5 × (x/2) + 0,5 × (2x) = 1,25 ×
Oletetaan, että alkuperäisessä kirjekuoressa oli 100 dollaria. Joten pitäisi olla 50 %:n todennäköisyys sille, että toisessa kirjekuoressa on 2 × 100 dollaria = 200 dollaria, ja 50 %:n todennäköisyys sille, että toisessa kirjekuoressa on (1/2) × 100 dollaria = 50 dollaria. Tällaisessa tapauksessa kirjekuoren arvo on:
0,5 × (100 $ / 2) + 0,5 × (2 × 100 $) = 125 $
Tämä tarkoittaa, että mies kasvattaisi varallisuuttaan keskimäärin 25 % pelkästään vaihtamalla kirjekuorta! Miten tämä voi olla mahdollista?
Tämä vaikuttaa matemaattiselta paradoksilta, mutta on todellisuudessa vain odotusarvokaavan väärinkäyttöä. Kuten kysymyksessä totesit, vaikuttaa siltä, että toisessa kirjekuoressa pitäisi olla 25 % enemmän kuin valitsemassasi. Jos kuitenkin uskot sen, voit yhtä hyvin valita aluksi toisen kirjekuoren. Lisäksi voisit käyttää tätä argumenttia vaihtaaksesi kirjekuoria loputtomiin, jos et ehdi avata kirjekuoria ennen vaihtopäätöstä. Odotusarvoargumentissa on selvästikin oltava jokin virhe. Kysymys kuuluu, missä virhe on?
Olen vuosien varrella käyttänyt paljon aikaa tämän ongelman lukemiseen ja siitä keskustelemiseen. Olen kuullut ja lukenut monia selityksiä siitä, miksi y=.5x + .5*2x = 1.25x -argumentti on väärä. Monet ovat käyttäneet selityksessä sivukaupalla edistynyttä matematiikkaa, minkä mielestäni ei ole tarpeen. Se on yksinkertainen kysymys, joka vaatii yksinkertaisen vastauksen. Joten tämä on minun kykyni siihen.
Sinun on oltava erittäin varovainen sen suhteen, mitä teet sen tosiasian kanssa, että toisessa kirjekuoressa on kaksi kertaa enemmän rahaa kuin toisessa. Kutsutaan pienemmän kirjekuoren summaa S:ksi ja suuremman kirjekuoren summaa L:ksi. Eli meillä on:
L=2×S
S=0,5×L
Huomaa, kuinka tekijöitä 2 ja 0,5 sovelletaan eri kirjekuoriin . Et voi ottaa molempia tekijöitä ja soveltaa niitä samaan summaan. Jos ensimmäisessä kirjekuoressa on 100 dollaria, niin jos se oli pienempi kirjekuori, toisessa on 200 dollaria. Jos 100 dollarin kirjekuori oli suurempi kirjekuori, niin toisessa on 50 dollaria. Joten toisessa kirjekuoressa on 50 dollaria tai 200 dollaria. Et kuitenkaan voi hypätä siitä ja sanoa, että molempien todennäköisyys on 50/50. Tämä johtuu siitä, että se tarkoittaisi tekijöiden 0,5 ja 2 soveltamista samaan summaan, mitä et voi tehdä. Ilman aluksi tietoa palkintojenjaosta et voi määrittää mahdollisia summia toiselle kirjekuorelle.
Jos 0,5x/2x-argumentti on väärin, niin miten toisen vaipan odotusarvo asetetaan oikein? Tekisin sen sanomalla, että kahden vaipan välinen erotus on LS = 2S - S = S. Vaihtamalla joko saat tai menetät S:n, olipa se mikä tahansa. Jos kahdessa vaipassa on 50 dollaria ja 100 dollaria, vaihtamalla saat tai menetät 50 dollaria. Jos kahdessa vaipassa on 100 dollaria ja 200 dollaria, vaihtamalla saat tai menetät 100 dollaria. Joka tapauksessa vaihtamalla odotettu voitto on 0. Voisin sanoa, että jos ensimmäisessä vaipassa on 100 dollaria, on 50 %:n todennäköisyys, että toisen vaipan erotus on 50 dollaria, ja 50 %:n todennäköisyys, että se on 100 dollaria. Joten odotettu erotus on 75 dollaria. Näin ollen toisen kirjekuoren odotusarvo on 0,5 × (100 $ + 75 $) + 0,5 × (100 $ - 75 $) = 0,5 × (175 $ + 25 $) = 100 $.
Toivottavasti tästä saa edes jotain selvää. Tämä ongelma herättää aina paljon kommentteja. Jos sinulla on sellainen, älä kirjoita minulle suoraan, vaan lähetä se Wizard of Vegas -foorumilleni. Linkki on alla.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Linkit
Tarkastellaan kolmen osapuolen kaksintaistelua, jossa osallistujat A, B ja C taistelevat kuolemaan asti naisesta. He ovat kaikki herrasmiehiä ja sopivat seuraavista säännöistä.
- Kolme osallistujaa muodostavat kolmion.
- Jokaisessa on vain yksi luoti.
- A menee ensin, sitten B ja C.
- A:n todennäköisyys osua aiottuun kohteeseen on 10 %.
- B:n todennäköisyys osua aiottuun kohteeseen on 60 %.
- C:n todennäköisyys osua aiottuun kohteeseen on 90 %.
- Vahingossa tapahtuneita ampumisia ei ole.
- Ilmaan ampuminen (tahallisesti ohi) ja itsensä ampuminen on sallittua, ja ne onnistuvat aina.
- Jos kierroksen jälkeen on jäljellä kaksi tai kolme eloonjäänyttä, jokaiselle annetaan uusi luoti. Sen jälkeen he ampuvat vuorotellen samassa järjestyksessä ohittaen kaikki jo kuolleet.
- Kaikki kolme osallistujaa ovat täydellisiä loogikoita.
Kehen A:n tulisi aluksi tähdätä? Mikä on hänen selviytymistodennäköisyytensä kullakin alkuperäisellä kohteella?
Tätä pulmaa käsitellään BBC:n ohjelmassa Quite Interesting . Vieritä 100 riviä alaspäin nähdäksesi vastauksen ja ratkaisun.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Tässä ovat A:n voittotodennäköisyyteni kunkin alkuperäisen kohteen mukaan. Kuten näette, A:n voittotodennäköisyys maksimoidaan ampumalla tarkoituksella ilmaan.
Truel-kertoimet
| Strategia | Todennäköinen voitto |
| Ilma | 13,887 % |
| A | 0,000 % |
| B | 12,560 % |
| C | 13,094 % |
Ratkaisussa käytetään merkintää Pr(X) merkitsemään todennäköisyyttä, että ryhmä X ja vain ryhmä X on jäljellä kierroksen jälkeen. Käytetään terminologiaa Pr(X*) merkitsemään todennäköisyyttä, että ryhmä X lopulta voittaa kierroksen toistettuaan, kunnes pelin tila muuttuu jonkun osuman vuoksi. Olkoon Pr(X**) todennäköisyys, että pelaaja X on ainoa selviytyjä. Lopullisten todennäköisyyksien löytämiseksi tarkastellaan ensin kahden pelaajan tiloja. On selvää, että molemmat ampuvat toisiaan kohti.
A vastaan B
- Pr(A) = 0,1
- Pr(B) = 0,9 × 0,6 = 0,54
- Pr(AB) = 0,9 × 0,4 = 0,36
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0,1/0,64 = 0,15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0,54/0,64 = 0,84375
A vs. C
- Pr(A) = 0,1
- Pr(C) = 0,9 × 0,9 = 0,81
- Pr(AC) = 0,9 × 0,1 = 0,09
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0,1/0,91 = 0,10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0,81/0,91 = 0,89010989
B vs. C
- Pr(B) = 0,6
- Pr(C) = 0,4 × 0,9 = 0,36
- Pr(BC) = 0,$×0,1 = 0,04
Jos molemmat selviävät, he toistavat, kunnes jäljellä on vain yksi. Joten viimeisen selviytyjän todennäköisyydet ovat:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0,6/,96 = 0,625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0,36/,96 = 0,375
Nyt olemme valmiita analysoimaan kolmen pelaajan tapausta. Tarkastellaan tilannetta, jossa A tähtää B:hen.
Kolme pelaajaa — A tähtää B:hen
Jos A osuu B:hen, C selviää varmasti hengissä ja saattaa osua A:han tai olla osumatta. B:n osumisesta on siis kaksi mahdollista lopputulosta: AC ja C. Jos A osuu ohi B:n, B tähtää suurempaan uhkaan C. Jos B osuu C:hen, A ja B selviävät. Jos B osuu C:hen, C tähtää suurempaan uhkaan B. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, A ja C selviävät. Mahdolliset lopputulokset ovat C, AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0,1 × 0,9 = 0,09. Tämä saavutetaan, kun A osuu B:hen ja sitten C osuu A:han.
- Pr(AB) = 0,9 × 0,6 = 0,54. Tämä saavutetaan, kun A osuu B:hen ohi ja sitten B osuu C:hen.
- Pr(AC) = 0,1 × 0,1 + 0,9 × 0,4 × 0,9 = 0,334. Tämä voidaan saavuttaa kahdella tavalla. Ensimmäinen on, että A osuu B:hen ja sitten C ohittaa A:n. Toinen on, että A ohittaa B:n, B ohittaa C:n ja sitten C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.964 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(C*) = 0,09/0,964 = 0,093361.
- Pr(AB*) = 0,54/0,964 = 0,560166.
- Pr(AC*) = 0,334/0,964 = 0,346473.
Kahden pelaajan tapauksista tiedämme, että jos ratkaisuksi jäävät A ja B, A voittaa todennäköisyydellä 0,15625 ja B 0,84375. Jos ratkaisuksi jäävät A ja C, A voittaa todennäköisyydellä 0,109890 ja C 0,890110.
- Pr(A**) = (0,560165975 × 0,15625) + (0,346473029 × 0,10989011) = 0,125600. A voi olla voittaja kahdella tavalla: (1) pääsemällä AB-tilaan ja voittamalla sitten tai (2) pääsemällä AC-tilaan ja voittamalla sitten.
- Pr(B**) = 0,560166 × 0,84375 = 0,472640. B voittaa, jos se pääsee AB-tilaan, ja silloin B voittaa.
- Pr(C**) = 0,093361 + (0,346473 × 0,890110) = 0,401760. C voi voittaa joko tappamalla A:n ja sitten C tappamalla A:n ensimmäisellä kierroksella tai pääsemällä tilaan AC ja sitten C voittamalla.
Jos A:n strategiana on siis tähtäillä ensin B:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 12,56 %.
Kolme pelaajaa — A tähtää C:hen
Jos A osuu C:hen, B selviää varmasti hengissä ja saattaa osua A:han tai olla osumatta. C:n osumisen kaksi mahdollista lopputulosta ovat AB ja B. Jos A osuu C:hen ohi, B tähtää suurempaan uhkaan C. Jos B osuu C:hen, A ja B selviävät. Jos B osuu C:hen ohi, C tähtää suurempaan uhkaan B. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, A ja C selviävät. Mahdolliset lopputulokset ovat siis B, AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0,1 × 0,6 = 0,06.
- Pr(C) = 0.
- Pr(AB) = (0,1 × 0,4) + (0,9 × 0,6) = 0,04 + 0,54 = 0,58. Tämä voidaan saavuttaa kahdella tavalla.Ensimmäinen on A:n osuma C:hen ja sitten B:n A ohitus. Toinen on A:n B ohitus ja sitten B:n C-osuma.
- Pr(AC) = 0,9 × 0,4 × 0,9 = 0,324. Tämä saavutetaan, kun A osuu C:hen, B osuu C:hen ja C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,9 × 0,4 × 0,1 = 0,036. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.964 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(B*) = 0,06/0,964 = 0,062241.
- Pr(AB*) = 0,58/0,964 = 0,601660.
- Pr(AC*) = 0,324/0,964 = 0,336100.
Samalla logiikalla kuin A:n ratkaisu pyrkii B:hen:
- Pr(A**) = (0,601660 × 0,15625) + (0,336100 × 0,10989011) = 0,130943.
- Pr(B**) = 0,062241 + 0,601660 × 0,84375 = 0,569891.
- Pr(C**) = 0,336100 × 0,890110 = 0,299166.
Jos siis A:n strategiana on tähtäillä ensin C:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 13,09 %.
Kolme pelaajaa – A heittää tahallaan ohi
Kun A osuu tahallaan ohi, B tähtää suurempaa uhkaa C:tä kohden. Jos B osuu C:hen, sekä A että B selviävät. Jos B osuu C:hen, C tähtää suurempaa uhkaa B:tä kohden. Jos C osuu B:hen, kaikki kolme selviävät. Jos C osuu B:hen, sekä A että C selviävät. Mahdolliset lopputulokset ovat AB, AC ja ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0,6. Tämä saavutetaan, kun B osuu C:hen.
- Pr(AC) = 0,4 × 0,9 = 0,36. Tämä saavutetaan, kun B osuu C:hen ja sitten C osuu B:hen.
- Pr(BC) = 0.
- Pr(ABC) = 0,4 × 0,1 = 0,04. Tämä saavutetaan, kun kaikki kolme puuttuvat.
Samalla logiikalla kuin kahden pelaajan tapauksissa, voimme jakaa jokaisen lopputuloksen luvulla (1-Pr(ABC))=0.96 löytääksemme kunkin tilan todennäköisyydet olettaen, että pelin tila muuttui kierroksen jälkeen.
- Pr(AB*) = 0,6/0,96 = 0,625.
- Pr(AC*) = 0,36/0,96 = 0,375.
Samalla logiikalla kuin A:n ratkaisu pyrkii B:hen:
- Pr(A**) = (0,625 × 0,15625) + (0,375 × 0,109890) = 0,138865.
- Pr(B**) = 0,625 × 0,84375 = 0,527344.
- Pr(C**) = 0,375 × 0,890110 = 0,333791.
Jos siis A:n strategiana on tähtäillä ensin C:hen, hänen todennäköisyytensä olla ainoa selviytyjä on 13,89 %.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Kun vertaillaan kahta elementtiä kerrallaan, mikä on nopein tapa lajitella lista minimoimalla vertailujen enimmäismäärä?
On olemassa useita tapoja, jotka ovat suunnilleen yhtä hyviä. Mielestäni helpoimmin ymmärrettävä on kuitenkin yhdistämislajittelu . Näin se toimii:
- Jaa lista kahtia. Jatka jokaisen osajoukon jakamista kahtia, kunnes jokainen osajoukko on kooltaan 1 tai 2.
- Lajittele jokainen 2:n osajoukko asettamalla pienempi jäsen ensimmäiseksi.
- Yhdistä osajoukkoparit yhteen. Toista, kunnes jäljellä on vain yksi lajiteltu lista.
Kahden listan yhdistäminen on vertailla kummankin listan ensimmäistä jäsentä ja sijoittaa pienempi jäsen uuteen listaan. Toista sitten tämä ja sijoita pienempi jäsen edellisen vertailun pienemmän jäsenen jälkeen. Toista, kunnes kaksi ryhmää on yhdistetty yhdeksi lajitelluksi ryhmäksi. Jos toinen alkuperäisistä kahdesta listasta on tyhjä, voit lisätä toisen listan yhdistetyn listan loppuun.
Seuraava taulukko näyttää vertailujen enimmäismäärän listan alkioiden lukumäärän mukaan.
Yhdistä lajittelu
| Elementit | Maksimivertailut |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1 793 |
| 512 | 4 097 |
| 1 024 | 9 217 |
| 2 048 | 20 481 |
| 4 096 | 45 057 |
| 8 192 | 98 305 |
| 16 384 | 212 993 |
| 32 768 | 458 753 |
| 65 536 | 983 041 |
| 131 072 | 2 097 153 |
| 262 144 | 4 456 449 |
| 524 288 | 9 437 185 |
| 1 048 576 | 19 922 945 |
| 2 097 152 | 41 943 041 |
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
The Las Vegas Review Journal julkaisi 29. lokakuuta 2010 Reidin ja Anglen välistä senaatinvaalia koskevan kyselyn. Siinä todettiin, että 625 todennäköisen äänestäjän kyselyssä Angle voitti 49 % ja Reid 45 % äänistä. Siinä myös todettiin, että virhemarginaali oli 4 %. Tässä ovat kysymykseni:
- Mikä on Anglen voittotodennäköisyys?
- Mikä olisi 95 %:n luottamusväli Anglen ääniosuudelle?
- Mitä virhemarginaali tarkoittaa?
Pahoittelen vanhentunutta vastausta tähän. Kirjoitin seuraavan ennen vaaleja.
Ensin aion päästä eroon niistä kuudesta prosentista, jotka ovat joko epävarmoja tai tuhlaavat äänensä kolmannen osapuolen ehdokkaaseen tai "ei mihinkään yllä mainituista", mikä on vaihtoehto Nevadassa. Jotkut saattavat olla eri mieltä tästä oletuksesta. Rehellisesti sanottuna toinen syy heidän jättämiseensä huomiotta on se, että matematiikka monimutkaistuu, kun ehdokkaita on enemmän kuin kaksi. Pyöristämisen jälkeen meille jäisi siis 306 ääntä Anglelle ja 281 ääntä Reidille, joten otoksessa on yhteensä 587 ääntä.
Aion käyttää standardinormaaliapproksimaatiota vastatakseni tähän kysymykseen. Jos olisin perfektionisti, käyttäisin t-jakaumaa , koska todellista keskiarvoa ja varianssia en tunneta. Mielestäni 587 otoskoko on kuitenkin täysin riittävä normaalijakaumalle.
Otoksen koko = 306 + 281 = 587.
Kulmanäytteen keskiarvo on 306/587 = 0,521295.
Keskiarvon arvioitu keskihajonta on (0,521295 × 0,478705 / (587-1))^0,5 = 0,0206361.
Kulman osuus yli 50 %:n on (0,521295-0,5) / 0,0206361 = 1,031917 keskihajontaa.
Normaalijakauman mukaan Reidin todennäköisyys sijoittua 1,031917 keskihajontaa odotettua pidemmälle on 0,151055. Tämä löytyy Excelistä funktiolla NORMSDIST(-1,031917). Joten Anglen voittotodennäköisyys on 1-0,151268 = 84,89 %.
95 %:n luottamusvälin luomiseksi huomioi, että Gaussin käyrän kummallakin puolella olevat 2,5 %:n pisteet ovat 1,959964 standardipoikkeaman kohdalla keskiarvosta. Tämä löytyy Excelistä funktiolla NORMSINV(0,975). Kuten jo todettiin, otoksen keskiarvon arvioitu standardipoikkeama on 0,0206361. Joten on 95 %:n mahdollisuus, että kumpi tahansa ehdokas pääsee kyselyn tuloksista 0,0206361 × 1,959964 = 0,040446 standardipoikkeaman sisälle. Joten Anglen 95 %:n luottamusväli on 0,521295 +/- 0,040446 = 48,08 % - 56,17 %.
Minulle on kerrottu, että olisi matemaattisesti virheellistä muotoilla "Anglen osuus kaikista Anglen/Reidin äänistä sijoittuu 95 %:n todennäköisyydellä 48,08 %:n ja 56,17 %:n välille". Näin alun perin muotoilin vastaukseni, mutta kaksi tilastotieteilijää kavahti kauhuissaan sanamuotoani. Heidän vastaustaan mukaillen he sanoivat, että minun piti käyttää passiivimuotoa ja sanoa, että "48,08 % ja 56,17 % ympäröivät Anglen osuuden 95 %:n todennäköisyydellä". Ollakseni rehellinen, se kuulostaa minusta samalta. He kuitenkin korostivat, että luottamusväli on satunnainen ja Anglen osuus on muuttumaton, ja että alkuperäinen sanamuotoni vihjasi päinvastaiseen. Joka tapauksessa toivon, että frekventistitilastotieteilijät ovat tyytyväisiä toiseen sanamuotoon.
" Virhemarginaali " on puolet 95 %:n luottamusvälin kahden ääripään välisestä erotuksesta. Tässä tapauksessa (56,17 % - 48,08 %) / 2 = 4,04 %.
Jatkossa, tässä ovat varsinaiset tulokset:
Reid: 361 655
Kulma: 320 996
Muut: 21 979
Joten, jos "muita" ääniä ei lasketa mukaan, Reid sai 53,0 % ja Angle 47,0 %. Se on mukava 6 %:n voitto Reidille. Se herättää kysymyksen, miksi kyselyn tulos oli niin kaukana todellisuudesta. Oliko se sattumaa? Muuttivatko äänestäjät mielensä? Vai oliko kyseessä alun perin huono kysely? Jätän nämä kysymykset lukijan pohdittavaksi (vihaan sitä, kun oppikirjat sanovat niin).
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Kokeilin vakuutusmatemaattista laskuriasi. Miksi todennäköisyys saavuttaa odotettu kuolinikäni on alle 50 %?
Sekoitat keskiarvon ja mediaanin. Katsotaanpa esimerkkinä minun tilannettani. Olen 45-vuotias mies. Elinajanodotteeni on 78,11 vuotta, mutta minulla on 50,04 %:n mahdollisuus elää 80-vuotiaaksi.
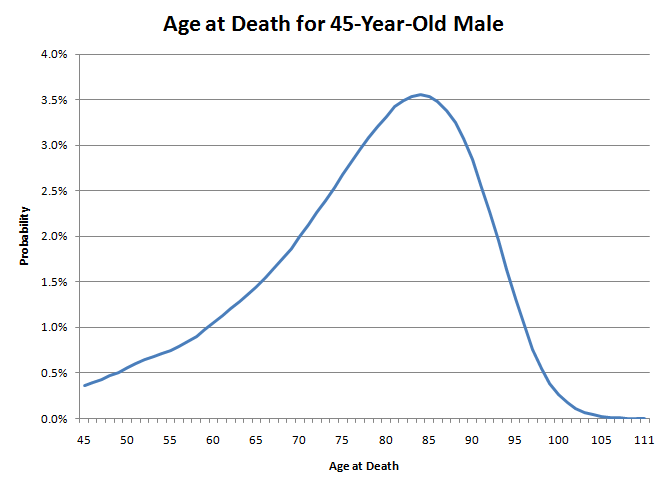
Kuolinikäni on kuin heittäisi tikanheittoa tähän käyrään. Huomaa, kuinka vasen häntä on paljon lihavampi kuin oikea. Tämä tarkoittaa, että kuolemani todennäköisyys juuri nyt on melko pieni. Vanhetessani kuoleman todennäköisyys seuraavana vuonna kuitenkin kasvaa jatkuvasti. Esimerkiksi 45-vuotiaalla miehellä todennäköisyys selvitä 46-vuotiaaksi on melko korkea, 99,64 %. Kuitenkin 85-vuotiaana todennäköisyys selvitä 86-vuotiaaksi on vain 89,21 %. Se on kuin luonto työntäisi hitaasti veistä selkään. Aluksi se ei luultavasti tapa sinua, mutta joka vuosi todennäköisyys sille kasvaa hitaasti. Kuitenkin, kun pääset 70-luvun lopulle, luonto sanoo, että riittää peleillä, ja alkaa todella tunkeutua peliin.
Jos siis paljon 45-vuotiaita miehiä heittää tikkaa tähän kaavioon, 49,96 % osuu 45–79-vuotiaisiin ja 50,04 % 80–111-vuotiaisiin. Onnekas puolisko, joka pääsee kaavion oikealle puolelle, ei kuitenkaan todennäköisesti elä paljon yli 80 vuoden iän. Kun mies täyttää 80 vuotta, hän voi odottaa elävänsä vain 7,78 vuotta pidempään. Samaan aikaan monet epäonnisesta puoliskosta, jotka eivät elä 80 ikävuoteen, kuolevat paljon nuorempina. Joten juuri monet nuoret kuolemat laskevat keskimääräistä elinajanodotetta.
Samankaltaisessa tilanteessa tarkastellaan noppaa, jonka numerot ovat 10, 20, 30, 31, 32, 33. Keskiarvo on 26, mutta on 2/3 mahdollisuus saada enemmän.
Esimerkkinä keskiarvon ja mediaanin eroista oletetaan, että lisäämme otokseen kaksi kuolemantapausta lisää. Yksi kuolema 46-vuotiaana ja yksi 81-vuotiaana. Todennäköisyys selvitä 80-vuotiaaksi ei muutu, mutta keskimääräinen elinajanodote 45-vuotiaana lyhenisi.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Kuvittele äärettömän elastinen kuminauha, joka on venyttämättömänä 1 km pitkä. Se laajenee nopeudella 1 km sekunnissa. Kuvittele seuraavaksi muurahainen kuminauhan toisessa päässä. Sillä hetkellä, kun kuminauha alkaa laajentua, muurahainen ryömii toista päätä kohti nopeudella, suhteessa nykyiseen sijaintiinsa, 1 cm sekunnissa. Pääseekö muurahainen koskaan toiseen päähän? Jos pääsee, niin milloin?
Kyllä, se tulee olemaan, 100 000 -1 sekunnin kuluttua. Katso mathproblems.info -sivustoltani tehtävästä 206 kaksi ratkaisua.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Onko hybridin parempi polttoainetehokkuus mielestäsi lisäkustannusten arvoinen? Kuinka monta kilometriä pitäisi ajaa, jotta pääsisi omilleen?
Hyvä kysymys. Vastatakseni siihen harkitsin Toyota Highlanderia, jota olen harkitsemassa ostavani. Vakiomallin hybridimallin vähittäismyyntihinta on 37 490 dollaria. Saman nelivetoisen auton ilman hybridiä hinta on 29 995 dollaria. Hybridimoottori lisää siis hintaan 7 495 dollaria.
Hybridin polttoaineenkulutus on 45 km/h sekä kaupungissa että maantiellä. Tavallisen auton polttoaineenkulutus on 17 km/h kaupungissa ja 22 km/h maantiellä. Otetaan keskiarvoksi 19,5 km/h.
Yleinen kaava kannattavuusrajan saavuttamiseen tarvittavien mailien lukumäärälle on h×m h ×m r /(g×(m h -m r )), jossa
h = Hybridin lisäkustannukset.
g = Bensiinin hinta gallonaa kohden.
m r = Ei-hybridiauton kilometrimäärä ("r" on tavalliselle autolle).
m h = Hybridin ajokilometrit.
Seuraavassa taulukossa käytetään tätä kaavaa löytääkseen kannattavuusrajan eri bensiinin hinnoille 2–5 dollariin gallonalta.
Hybridi-yhtiöiden kannattavuusraja
| Bensiinin hinta | Mailien määrä |
| 2,00 dollaria | 240 722 |
| 2,25 dollaria | 213 975 |
| 2,50 dollaria | 192 577 |
| 2,75 dollaria | 175 070 |
| 3,00 dollaria | 160 481 |
| 3,25 dollaria | 148 136 |
| 3,50 dollaria | 137 555 |
| 3,75 dollaria | 128 385 |
| 4,00 dollaria | 120 361 | 4,25 dollaria | 113 281 |
| 4,50 dollaria | 106 987 |
| 4,75 dollaria | 101 357 |
| 5,00 dollaria | 96 289 |
Joten nykyisellä 3,00 dollarin gallonahinnalla täällä Vegasissa ajoneuvolla pitäisi ajaa yli 160 481 mailia menestyäkseen. Tämä ei sisällä muita hybridiin mahdollisesti liittyviä kuluja, kuten akkujen kalliita vaihtokustannuksia, eikä fossiilisten polttoaineiden kulutuksen vähentämisestä saatavia vihreitä pisteitä.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Mikä geenien suhde minulla olisi yhteistä täyssisaren kanssa, joka ei ole identtinen kaksos?
1/2.
Jos käyttäisimme vertailukohtana kenoa, jokaisella olisi 40 geeniä, joita kutakin edustaisi yksi kenopallo. Jokaisella pallolla olisi kuitenkin yksilöllinen numero. Kun kaksi ihmistä, jotka eivät ole sukua toisilleen, parittelee, se on kuin yhdistäisi 80 palloa heidän välillään suppiloon ja valitsisi satunnaisesti 40 geeniä parittelun jälkeläisille.
Joten kun sinut hedelmöitettiin, puolet palloista meni suppiloon ja toinen puoli meni hukkaan. Kun veljesi tai sisaresi hedelmöittyi, hän sai puolet syntymäsi yhteydessä arvotuista palloista ja puolet niistä, joita ei arvottu. Olette siis geneettisesti 50 % identtisiä. Paljolti samasta syystä kuin jos kenossa arvottaisiin 40 numeroa, kahdessa peräkkäisessä arvonnassa olisi keskimäärin 20 yhteistä palloa.
Tätä kysymystä käsiteltiin kumppanisivustoni Wizard of Vegasin foorumilla.
Pöytiä ja tuoleja valmistavassa tehtaassa on 10 sahaa, 6 sorvia ja 18 hiomakonetta. Tuolin hiominen sahalla kestää 10 minuuttia, sorvilla 5 minuuttia ja hiominen 5 minuuttia. Pöydän hiominen sahalla kestää 5 minuuttia, sorvilla 5 minuuttia ja hiominen 20 minuuttia. Tuolin hinta on 10 dollaria ja pöydän hinta 20 dollaria. Kuinka monta pöytää ja tuolia tehtaan pitäisi tuottaa tunnissa, jotta se saisi suurimman tulon, ja mikä tämä tulo on?
Olkoon c tunnissa valmistettujen tuolien lukumäärä ja t pöytien lukumäärä. Tuntituloksi saadaan 10×c + 20×t.
Kymmenen sahaa tarkoittaa 600 minuuttia sahaamista tunnissa. Meille annettiin, että tuolin sahausaika on 10 minuuttia ja pöydän 5 minuuttia. Tämä rajoittaa tunnissa tapahtuvan tuotannon seuraavasti:
(1) 10c + 5t <= 600
Kuusi sorvia vastaavat 360 minuuttia sorvausta tunnissa. Meille annettiin, että tuolin sahausaika on viisi minuuttia ja pöydän vastaava viisi. Tämä rajoittaa tunnissa tapahtuvan tuotannon seuraavasti:
(2) 5c + 5t <= 360
18 hiomakonetta tuottavat 1080 minuuttia hiontaa tunnissa. Meille annettiin, että tuolin sahausaika on 5 minuuttia ja pöydän 20. Tämä rajoittaa tunnissa tapahtuvan tuotannon seuraavasti:
(3) 5c + 20t <= 1080
Seuraava kaavio näyttää kolmen konesarjan asettamat kolme rajoitusta. Tehdas voi tuottaa minkä tahansa yhdistelmän tuoleja ja pöytiä, jotka ovat kaikkien kolmen linjan alla. Kysymys kuuluu, missä kolmen linjan alla saadaan suurin tulo.
On loogista, että vastaus olisi kahden suoran leikkauspiste, teemmekö kaikki tuolit vai teemmekö kaikki pöydät. Etsitään siis, missä suorat leikkaavat. Ensin etsitään, missä yhtälöt (1) ja (2) leikkaavat toisensa. Voimme muuttaa <= -lausekkeen muotoon =, jotta voimme hyödyntää koneita parhaalla mahdollisella tavalla.
(1) 10c + 5t = 600
(2) 5c + 5t = 360
Vähennä (2) kohdasta (1):
5c = 240
c = 48
Kytketään c:n arvo 48 yhtälöön (1):
10 × 48 + 5t = 600
5t = 120
t = 24
Yhtälöt (1) ja (2) siis kohtaavat 48 tuolin ja 24 pöydän kohdalla.
Seuraavaksi katsotaan, missä yhtälöt (2) ja (3) kohtaavat:
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
Vähentämällä (2) kohdasta (3):
15t = 720
t = 48
Sijoittamalla sen yhtälöön (2) tai (3), voimme ratkaista c:n, joka on 24.
Yhtälöt (2) ja (3) siis kohtaavat 24 tuolin ja 48 pöydän kohdalla.
Meidän ei tarvitse vaivautua etsimään yhtälöiden (1) ja (3) yhtymäkohtia, koska kaaviosta näemme, että sahan ja hiomakoneen viivojen yhtymäkohta on sorvin rajoitteen ulkopuolella.
On myös mahdollista, että pelkkien tuolien valmistaminen on oikea vastaus. Kaavio osoittaa, että sahat ovat suurin rajoitus pelkkien tuolien valmistamiselle. Yhtälöstä (1) jos asetamme pöytien lukumääräksi 0, saamme c=60.
Toinen mahdollisuus on tehdä pelkkiä pöytiä. Kaavio osoittaa, että hiomakoneet ovat suurin rajoitus. Laittamalla yhtälöön (3) 0 tuolia, huomaamme, että voimme tehdä enintään 54 pöytää.
Seuraava kaavio näyttää kunkin pätevän vastauksen kokonaisliikevaihdon. Muista, että liikevaihdoksi tulee 10 dollaria tuolia kohden ja 20 dollaria pöytää kohden.
Kokonaistuntituotto
| Tuolit | Pöydät | Tulot |
| 0 | 54 | 1 080 dollaria |
| 24 | 48 | 1 200 dollaria |
| 48 | 24 | 960 dollaria |
| 60 | 0 | 600 dollaria |
Kuninkaalla on tynnyri täynnä viiniä.
Maanantai-iltana palvelija varastaa tynnyristä kolme kuppia ja korvaa ne kolmella kupillisella vettä.
Tiistai-iltana toinen palvelija varastaa kolme kuppia nyt laimennettusta viinitynnyristä ja korvaa ne kolmella kupilla vettä.
Keskiviikkoiltana jälleen yksi palvelija varastaa kolme kuppia nyt laimeammasta viinitynnyristä ja korvaa ne kolmella kupillisella vettä.
Torstaiaamuna tynnyrissä on 50 % viiniä ja 50 % vettä.
Kuinka paljon viiniä oli alun perin tynnyrissä?
Tässä on vastaus ja ratkaisu (PDF).
Jos haluat keskustella tästä ongelmasta, käy foorumillani Wizard of Vegasissa .
Jos minulla olisi kulhollinen 200 Skittles-muroa ja 3 niistä tappaisi minut, mitkä ovat todennäköisyydet, että kuolisin, jos ottaisin kourallisen 12 Skittles-muroa ja söisin ne kaikki? Olettaen, että minut tappaa vain yksi myrkkymuro.
Lisätietoja tästä kysymyksestä saat foorumiltani Wizard of Vegasissa .
Muukalainen on siepannut kymmenen loogikkoa ja sijoittanut heidät huoneeseen. Hän selittää heille, että hän ensin järjestää heidät riviin pisimmästä lyhyimpään siten, että jokainen henkilö on kasvot seuraavaksi lyhimmän edessä olevan henkilön suuntaan, jotta jokainen henkilö näkee kaikki lyhyemmät loogikot, mutta ei pidempiä. Sitten hän selittää, että hän asettaa mustan tai valkoisen hatun jokaiselle henkilölle, mutta kukaan ei näe hänen oman hatunsa väriä, vain lyhyempien loogikkojen hatut. Mustavalkoisten hattujen jakauma voi olla mikä tahansa, ei välttämättä viisi ja viisi.
Sitten avaruusolento selittää, että hän kysyy jokaiselta loogikolta, aloittaen pisimmästä ja edeten riviä alaspäin, hänen hatunsa värin. Loogikot saavat kuulla edellään toimivien vastauksen. Mustavalkoisia vastauksia lukuun ottamatta he eivät saa kommunikoida millään tavalla pelin alettua. Jos useampi kuin yksi loogikko on väärässä, heidät kaikki syödään. Jos vähintään yhdeksän vastausta on oikein, heidät palautetaan turvallisesti maan pinnalle. Avaruusolento antaa heille sitten aikaa strategian laatimiseen. Mikä heidän strategiansa tulisi olla?
Seuraavassa on yksi mahdollinen strategia. Ensimmäisenä toimivan loogikon on sanottava "musta", jos hän näkee parillisen määrän mustia hattuja, ja "valkoinen", jos hän näkee parittoman määrän muita yhdeksää loogikkoa. Hänellä on 50 %:n mahdollisuus saada samanvärinen hattu kuin hänen omassa, joten hän on ainoa, joka saa olla väärässä. Mitä tahansa hän sanookin, määrittele se "juoksevaksi väriksi".
Seuraavaksi toiseksi vuorossa oleva loogikko laskee kahdeksan lyhyemmän loogikon mustat hatut ja yhdistää ne väriin samalla parittomalla ja parillisella menetelmällä kuin ensimmäinen loogikko. Jos tämä on yhdenmukainen ensimmäisen loogikon ilmoittaman värin kanssa, hänellä on oltava valkoinen hattu ja hänen tulee sanoa valkoinen. Jos se on erilainen, hänellä on oltava musta hattu ja hänen tulee sanoa musta. Jos hän sanoo "valkoinen", juokseva väri pysyy samana. Jos hän sanoo "musta", juokseva väri vaihtuu vastakkaiseksi väriksi.
Seuraavaksi kolmas loogikko tekee täsmälleen kuten toinen, mutta laskee seitsemän lyhyemmän loogikon mustat hatut. Samoin, jos hän on samaa mieltä juoksevan värin kanssa, hän sanoo "valkoinen" ja juokseva väri pysyy samana. Jos hän on eri mieltä juoksevan värin kanssa, hän sanoo "musta" ja juokseva väri vaihtuu.
Jokainen muu loogikko tekee täsmälleen saman asian.
Tietenkin he voisivat yhtä hyvin yhdistää mustan parittomalle luvulle ja valkoisen parilliselle luvulle. Tärkeintä on, että he kaikki ovat yhtä mieltä siitä, mikä väri tarkoittaa mitä paritonta/parillista lukua. Kumman tahansa strategian noudattaminen johtaa siihen, että toisesta kymmenenteen toimimaan ryhtyvät loogikot ovat kaikki oikein ja ensimmäisellä on 50 %:n mahdollisuus, joten he kaikki selviävät. Tämä strategia toimii mille tahansa määrälle loogikoita.
Axelilla ja Bobilla on kummallakin omat 52 kortin pakkansa. Molemmat sekoittavat ne satunnaisesti. Sitten he kääntävät yhden kortin kerrallaan, samanaikaisesti, kummastakin pakasta. Mikä on todennäköisyys, että he kääntävät saman kortin samaan aikaan ainakin kerran?
Vastaus olisi helppo arvioida muotoon 1-(51/52) 52 = 0,63568648. Arviot ovat kuitenkin älyllisesti niin epätyydyttäviä. Joten etsitään tarkka ratkaisu!
Vaihe 1: Aloita miettimällä, kuinka monella tavalla toinen pakka voidaan järjestää, kun ensimmäinen kortti on numero 1. Vastaus on kuinka monella tavalla muut 51 korttia voidaan järjestää, eli 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Mikä tahansa kortti voi sopia ensimmäiseen pakkaan, joten meidän on tehtävä tämä kaikille 52 kortille. Tämä antaa meille 52 * 51! = 52! yhdistelmää, joissa ainakin yksi kortti sopii.
Vaihe 2: Vaiheessa 1 kuitenkin lasketaan kaksinkertaisesti jokainen tilanne, jossa kaksi korttia on samanarvoisia. Esimerkiksi, jos kaksi ensimmäistä korttia olisivat 1 ja 2, olisimme laskeneet 50! tapaa järjestää muut kortit kahdesti, kerran siten, että 1 olisi ensimmäinen kortti ja toisen kerran siten, että 2 olisi toinen kortti. Tapojen lukumäärä 2 kortille 52:sta on combin(52,2) = 1326. Jokaista kahden kortin yhdistelmää kohden on 50! = 3041409320171337804361260816606476884437764156896051200000000000000 tapaa järjestää muut kortit. Näin ollen vaiheessa 2 meidän on vähennettävä combin(52,2)*50! = (52*51/2!)*50! = 52!/2! yhdistelmät.
Vaihe 3: Tarkastellaan seuraavaksi tilannetta, jossa satunnaispakan kolme ensimmäistä korttia ovat järjestyksessä 1, 2 ja 3. Loput 49 korttia voidaan järjestää 49! eri tavalla. Ensimmäisessä vaiheessa olisimme laskeneet ne kolme kertaa, jotta löytäisimme ainakin yhden samanlaisen kortin. Sitten toisessa vaiheessa olisimme vähentäneet kaikki combin(3,2)=3 tapaa valita kaksi näistä kolmesta kortista. Joten tämä tilanne olisi laskettu 3 - 3 = 0 kertaa, joten meidän on lisättävä ne takaisin. On olemassa combin(52,3) tällaista tilannetta, joissa valitaan ainakin kolme samaa korttia. Joten meidän on lisättävä takaisin combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! yhdistelmät.
Vaihe 4: Tarkastellaan seuraavaksi tilannetta, jossa satunnaispakan neljä ensimmäistä korttia ovat järjestyksessä 1, 2, 3 ja 4. Loput 48 korttia voidaan järjestää 48! eri tavalla. Olisimme laskeneet ne neljä kertaa ensimmäisessä vaiheessa, jossa laskettiin ainakin yksi sama kortti. Sitten olisimme vähentäneet kaikki combin(4,2)=6 tapaa valita kaksi näistä neljästä kortista vaiheessa 2. Sitten olisimme laskeneet yhteen kaikki combin(4,3)=4 tapaa valita 3 näistä neljästä kortista. Joten olemme 4-6+4=2 tavalla, joilla jokainen tällainen tilanne olisi laskettu. Joten meidän on vähennettävä yksi näistä tavoista, jotta jokainen tilanne lasketaan kerran. On combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! tällaisia tilanteita, jotka on lisättävä takaisin.
Jatkamme tätä vuorotellen yhteen- ja vähennyslaskuja korjataksemme kaksinkertaisen laskennan.
Loppujen lopuksi tilanteiden lukumäärä, joissa ainakin yksi satunnaispakan kortti vastaa järjestettyä pakkaa = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
Kortteja voi tilata yhteensä 52! = y = 52717761549636521942261854154512265996921245386198220800000000000000 Yhteensä 52 kortin tilaustapoja.
Näin ollen vastaus on x/y = 0,6321205588285576784044762298
Todennäköisyys sille, ettei osumia löydy, on 1-(x/y) = 0,3678794411714423215955237702.
Jos tämä luku näyttää tutulta, sen pitäisikin näyttää tutulta. 1/e = 0,3678794411714423215955237702.
Joten vastaus voidaan arvioida HYVIN tarkasti muotoon 1-(1/e).
Kiitokset
Matemaattiset laskelmat tehtiin Pari/GP: ssä
Tätä ongelmaa kysyttiin ja siitä keskusteltiin foorumillani Wizard of Vegasissa .
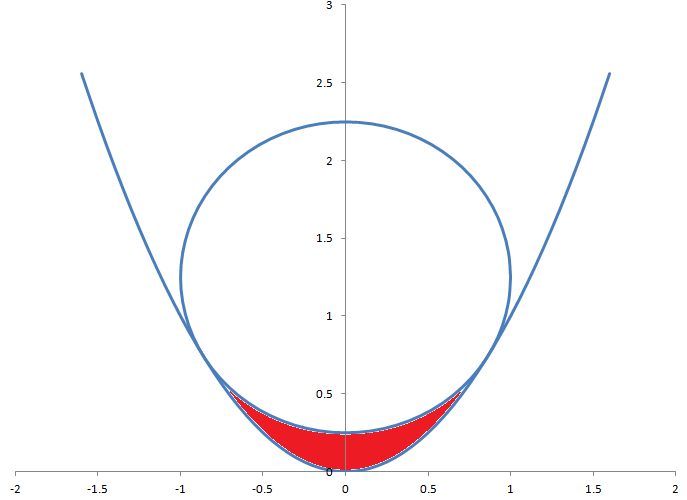
Säteeltään 1 oleva ympyrä on tangentti yhtälön y=x 2 mukaiselle paraabelille. Mikä on punaisella merkityn alueen pinta-ala ympyrän ja paraabelin välissä?
Klikkaa alla olevaa painiketta nähdäksesi vastauksen.
Tässä on ratkaisuni . (PDF)
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Sain tämän ongelman Presh Talwalkerilta Mind Your Decisionsista .
Kasinon jakaja työstää uutta Three Card Poker -varianttia. Hän ottaa kaikki kuvakortit tavallisesta pakasta ja sekoittaa ne huolellisesti. Sitten hän jakaa kolme korttia pelaajalle 1, kolme korttia pelaajalle 2, kolme korttia pelaajalle 3 ja loput kolme korttia pelaajalle 4. Mikä on todennäköisyys, että kaikissa neljässä kädessä on suora (JQK mistä tahansa maasta)?

Todennäköisyys sille, että ensimmäinen käsi on AKQ, on 1*(8/11)*(4/10) = 29,09%.
Todennäköisyys, että sekuntiviisari on AKQ, olettaen, että ensimmäinen viisari on jo AKQ, on 1 * (6/8) * (3/7) = 32,14 %.
Todennäköisyys sille, että kolmas käsi on AKQ, olettaen, että ensimmäinen ja toinen käsi ovat jo olemassa, on 1*(4/5)*(2/4) = 40,00 %
Jäljelle jäävien korttien on oltava AKQ, koska kolme ensimmäistä kättä ovat. Todennäköisyys on siis kolmen edellä mainitun todennäköisyyden tulo, joka on 216/5775 = noin 0,037402597.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Mikä on säteeltään 1 satunnaisesti piirretyn ympyrän sisään piirretyn suorakulmion keskimääräinen pinta-ala ja kehä?
Hyvä kysymys. Tässä ovat vastaukseni:
Tässä on ratkaisuni molempiin (PDF).
Etsi kymmennumeroinen luku, jolle on tyypillistä:
- Luvun ensimmäinen numero on nollien lukumäärä koko luvussa.
- Luvun toinen numero on ykkösten lukumäärä koko luvussa.
- Luvun kolmas numero on kakkosten lukumäärä koko luvussa.
- Luvun neljäs numero on 3:ien lukumäärä koko luvussa.
- Luvun viides numero on nelosten lukumäärä koko luvussa.
- Luvun kuudes numero on viitosten lukumäärä koko luvussa.
- Luvun seitsemäs numero on kuutosten lukumäärä koko luvussa.
- Luvun kahdeksas numero on seitsien lukumäärä koko luvussa.
- Luvun yhdeksäs numero on 8:ien lukumäärä koko luvussa.
- Luvun kymmenes numero on yhdeksiköiden lukumäärä koko luvussa.
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Kolme pistettä on sijoitettu satunnaisesti ja tasaisesti ympyrälle, jonka säde on 1. Mikä on odotettu pienin etäisyys kolmen pisteen välillä, kun etäisyydet mitataan ympyrän kehää pitkin?
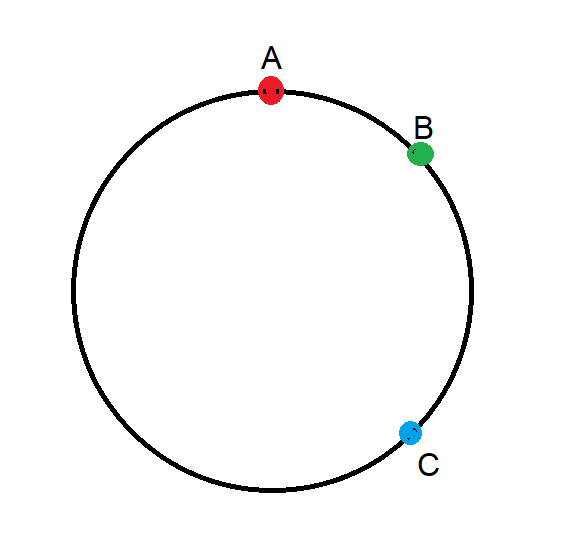
Tässä on ratkaisuni (PDF).
Tätä kysymystä on kysytty ja siitä on keskusteltu foorumillani Wizard of Vegasissa .
Alicella ja Billillä kestää talon maalaaminen kolme tuntia.
Alicella ja Cindyllä kestää talon maalaaminen neljä tuntia.
Billiltä ja Cindyltä kestää talon maalaaminen viisi tuntia.
Kuinka kauan kestää, jos kaikki maalaavat?
Tässä on ratkaisuni (PDF).


